FFT学习笔记
FFT,快速傅里叶变换,是一种在(O(nlog n))的时间内计算两个多项式乘积的算法。
前置芝士
复数
没学过的请自行翻阅高中数学选修2-2。
多项式的表示
给出一个多项式 $f(x) = a_0 + a_1x + a_2x^2 + ... + a_nx^n $
系数表示法
就是用一个系数序列来表达多项式,显然系数序列和多项式是一一对应的。
点值表示法
点值表示法是把这个多项式看成一个函数,从上面选取(n+1)个点,从而利用这 (n+1) 个点来唯一的表示这个函数。
正如解一个 (n) 元方程组需要 (n+1) 个方程一样,这 (n+1) 个点的序列显然也和多项式一一对应。
--------------------分割线--------------------
这两种表示法各有优劣,系数表示法可以在 (O(n)) 的时间内求出一个 (f(x_0)) ,但计算多项式乘法时却需要 (O(n^2)) 的时间,点值表示法则正好相反。所以FFT的目的就是利用一些特殊的点,把复杂度均摊一下,变成 (O(nlog n))
单位复根
这是FFT降低复杂度的关键,因为单位复根有极为优秀的性质。
定义:
对于方程 (x^n = 1) 的复数解,称之为 (n) 次单位复根,显然这样的单位复根有 (n) 个。
其中一个可以表示为 $ omega_n = e^{frac{2pi i}{n}} $ 那么对于每一个单位复根,有$$ omega_n^k = e^{frac{2pi i k}{n}} $$
而根据欧拉公式,又有:
几何意义:
在一个单位圆中,把单位圆等分,几个等分点的坐标就是单位复根的向量。
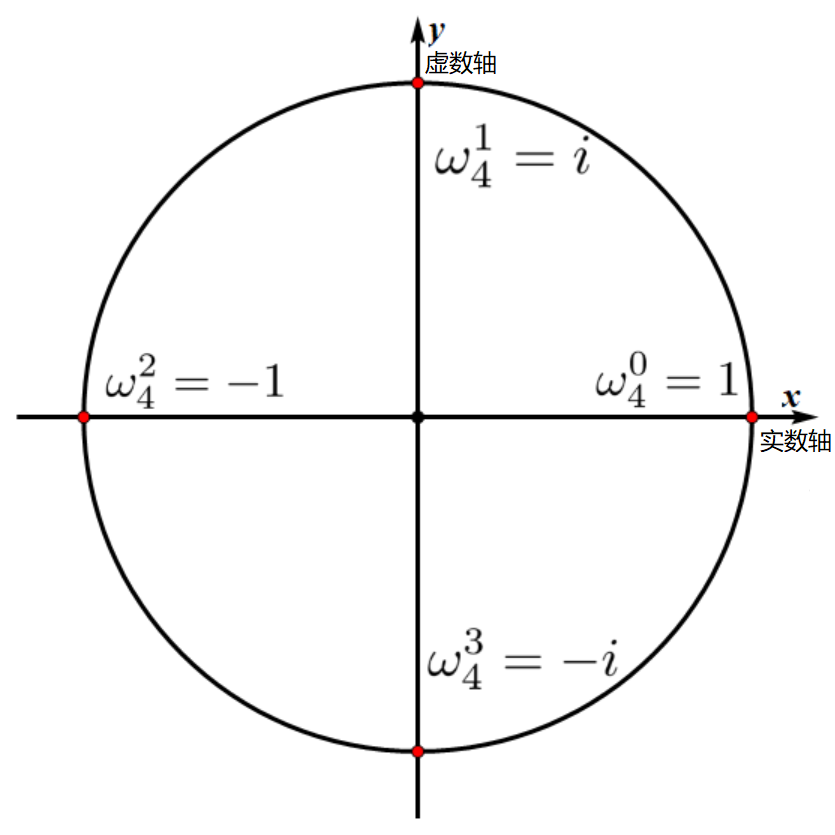
这个图就可以生动形象表示出来了。
单位根的性质
性质1:(omega_n^0 = 1)
这十分显然,看图就知道了。
性质2:(omega_n^k = omega_{2n}^{2k})
可以根据公式证明,或者几何意义也可直观理解。
性质3:(omega_n^{k+frac{n}{2}}=-omega_n^k)
仍然是代入公式证明即可。
这三个性质就是FFT降低复杂度的关键了。
快速傅里叶变换
离散傅里叶变换(DFT)
对于一个多项式 $f(x) = a_0 + a_1x + a_2x^2 + ... + a_{n-1}x^{n-1} $
为了便于操作,设 (n = 2^k)$ ,不足补0即可。
然后按照奇偶项分类,奇数项提出一个 (x):
设两个新的多项式:
那么就可以得到:
设(DFT(f(x)))表示对 (f(x)) 进行DFT操作后得到的点值表示,则:
重要的步骤出现了!这时我们依次代入单位复根:
同理:
我们发现,只要我们求出了(DFT(g(omega_{frac{n}{2}}^{k}))) 和 (DFT(h(omega_{frac{n}{2}}^{k}))),就可以求出 (DFT(f(omega_n^k))) 和 (DFT(f(omega_n^{k+frac{n}{2}}))),而这是一个问题规模不断变小的子问题,直接递归就行了。
复杂度分析:
代入操作要进行 (n) 次,花费 (O(n)) 的时间,设单次操作复杂度为 (T(n)),则有:
根据主定理,可得复杂度为 (O(n log n))
离散傅里叶逆变换(IDFT)
证明过程又臭又长,这里就不写了qwq。(参考链接)
只介绍算法:
对于一个点值序列:(f(x) = {(x_0,y_0),(x_1,y_1),(x_2,y_2),...,(x_n,y_n)})
进行的操作方法和DFT类似,只是每次代入(frac{1}{omega_n^k})即可。
化简一下:
(frac{1}{omega_n^k} = e^{-frac{2pi ik}{n}} = cos(frac{2 pi k}{n}) + i · sin(-frac{2 pi k}{n}))
我们注意到这个值和DFT代入的值仅仅只有符号上的区别,那么不妨定义一个变量(op),当 (op) 取 (1) 时进行 DFT操作,取 (-1) 就是IDFT操作。
代码实现:
void fft(comp *f,int n,int op) // op=1 -> DFT,op=-1 -> IDFT
{
if(n == 1) return;//递归边界
for(int i = 0;i < n;++i) tmp[i] = f[i];
for(int i = 0;i < n;++i)//奇偶分别处理
{
if(i & 1) f[i / 2 + n / 2] = tmp[i];
else f[i / 2] = tmp[i];
}
comp *g = f,*h = f + n / 2;
fft(g,n / 2,op);fft(h,n / 2,op);//递归
comp w(cos(2 * pi / n),sin(2 * pi * op / n)),x(1,0);//单位根
for(int k = 0;k < n / 2;++k)
{
tmp[k] = g[k] + x * h[k];
tmp[k + n / 2] = g[k] - x * h[k];
x *= w;
}
for(int i = 0;i < n;++i) f[i] = tmp[i];
return;
}
好的最朴素的FFT就讲完了。
FFT优化
咕咕咕咕咕咕咕咕咕