講講 John Carmack 的快速反平方根演算法
原地址http://213style.blogspot.com/2014/07/john-carmack.html
本篇的主題很簡單,講講怎麼快速計算 反平方根
圖1. 反平方根函數,但是要如何快速計算此式呢?
反平方根運算在 3D 圖形領域占有重要地位,主要用於計算 光源 與 反射,運算過程中
需要計算 Normalized Vector,這時就需要進行反平方根運算,因為在 1990 年以前可沒有
特殊的硬體可以直接處理 T&L,直到有名的 GeForce 256 出現才改觀,而 3D 遊戲內某些
可以貫穿多個敵人的武器,也需要用到反平方根運算,所以該運算不只出現在與繪圖有關
的部分,一些與圖形無關的演算法也會用到,所以大部分 3D 遊戲中,都還是會存在獨立的
反平方根函式。在數值計算領域裡,反平方根計算可以間接取得平方根的值,例如在 8051
這類只能運算整數的微處理器,要計算平方根就會用到反平方根運,因為 反平方根運 存在
快速演算法,其中最有名的就是在 Quake III 裡面的 Q_rsqrt 函式,這個函式非常有名,大不
分的 反平方根運算 都是直接把這段函式的原始碼直接貼到自己的程式內,然後在根據
需要修改,例如要用於 8051 內就還得需要加上定點化的技巧,目前顯示卡內硬體的反平方根
運算正是 Q_rsqrt 演算法硬體化的結果,所以先來看看這段在 Quake III 內 Q_rsqrt 的原始碼:
圖 2. 位於 Quake III 內的 Q_rsqrt 函式原始碼
中文註解部分是在下加上。
整個函式包含兩個部分:
第一部分, 從 整數運算 得到 一個已經 靠近解的初始值
第二不分, 利用 Newton-Raphson 方法疊代增加解的精度
該函式內演算法精髓的部分是在 第一部分 用整數運算取得求解所需的初始值,第二部分
到沒甚麼,有學過數值方法的讀著應該可以很輕易的看懂,但是對於沒有學過的讀者,在下
講完第一部分之後,會稍微提一下 Newton-Raphson 求解法,因為第二部分並非重點,理解
第一部分才是重點所在,第一部分用到的技巧涉及必須理解浮點數的存放結構與表達,所以
先看看浮點數怎麼存放在電腦中。
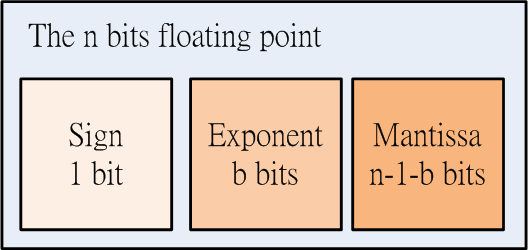
圖 3. 一個 n bits 的浮點數的存放結構
圖 4. 一個浮點數的表達
圖 3. 顯示了 一個浮點數如何存放在記憶體內,有時候又稱 floating-point bits level,各位讀者
可以看到一個端倪,其實浮點數也是一種整數,或者說每個浮點數都有獨一無二的整數映射
而圖 4. 說明了 浮點運算器怎麼解讀一個整數為浮點數的方式,由於反平方根不能有負值
所以圖 4. 中的 s 必須等於 0,因此就可以不用考慮浮點數的符號位元,剛剛前面有提到
其實浮點數也是一種整數,也就是說,假如圖 3. 的浮點數存放結構 改用整數的觀點來看
其實就是
圖 5. 浮點數 與 整數 的對應關係
圖 5. 說明 一個浮點數 與 對應的整數之間總是存在 唯一的對應關係,因此,可以將
浮點數映至對應的整數,從整數的觀點進行運算,要執行這個技巧之前,先以浮點數
觀點對兩邊做 Binary Logarithm,也就是兩邊取 2 為基底的 log 函數:
圖 6. 對兩邊取 log2,且 y 與 x 皆代入圖 4. 的方程式
圖 6. 將 y 與 x 皆拆解為 mantissa 與 exponent 表達,剩下的工作就是要找出 從整數觀點表達
的 y 與 x 之間的關係,所以必須想辦法先把 log2 弄掉,才能夠套用圖 5. 內的恆等式,而
圖 4. 裡面的浮點數表達式中的 m 是一個大於等於 0 小於 1 的數值,所以圖 6. 中要把 log2
拿掉 可以用 近似公式
圖 7. 近似的 binary logarithm 公式
如圖 7. 所示,利用近似 Binary Logarithm 公式,可以將圖 6. 中的 log 函數拿掉,用近似公式
替換,這個近似的步驟很重要,透過這個步驟才能夠獲得才能夠獲得等價於圖 1. 的整數
運算公式,其 圖 8. 顯示了完整的推導過程。
圖 8. 用整數運算式表達近似反平方根運算
圖 8. 最後一條公式就是這個演算法最重要的結論,這條整數運算的結果就是反平方根
用整數運算表達的形式,所以最終的結論可以用圖 9. 來解釋。
圖 9. 最終結論解釋了圖 1. 中神秘的轉換運算的理由,可以看到
該方法厲害之處在於 Iy 轉回浮點數觀點看,其實已經是近似解
這個近似解就是最好的初始值,後面套用牛頓法只是為了增加解的精度
有了圖 9. 最終結論,要理解圖 1. 中 16 進位值 5F3759DF 就很簡單,只要將 B、L 與 sigma
的數值代入圖 9. 的反平方根近似整數演算法就會得到這個 魔術數字。
圖 10. 神秘的 0x5F3759DF 魔術數字其實只是 32-bit 浮點
代入反平方根整數演算法所得到的結果,而且 sigma 可調
該魔術數字可能會有些微的變化
圖 10. 解釋了 John Carmack 快速反平方根演算法內 Magic Number 的由來,由於在下
是直接以 n 位元浮點數推導,讀者也可以去找一找 double floating 的值會是多少
演算法後面的部分前面有提到,其實沒有甚麼值得研究的部分,用牛頓法增加解精度
有學過數值方法的讀者應該可以看得懂,因為整數演算法只是一個近似解,所以需要
用牛頓法 " 修飾 " 一下解,下面給出用牛頓法推導所得之疊代式。
圖 11. 用牛頓法導出求解疊代式
整個演算法核心的部分講完,下面給出一支帶有 GUI 介面的測試程式,並且稍微介紹一下
在下如何用 Tick 量測演算法所增進的效率。
圖 12. 兩種方法各執行 一百萬 次 用 GetTickCount
量測所經過的 Tick 數
從這支 GUI 測試可以發現,x86 CPU 是屬於 " 不穩定 " 的處理器,就是說要精確量測 x86
CPU 所經過的 cycle 數是不可能的事情,主要因為現在 x86 CPU 很複雜,內部有許多快取
預測的架構,所以同樣一支程式的執行時間會忽快忽慢,用這支程式就可以很明顯發現
這個現象,在 x86 平台上 Carmack 的快速反平方根演算法會比用標準數學程式庫算
1/sqrt(x) 可能快 1.5x ~ 4x,x86 CPU 很聰明,假如曾經有計算過的某些數值,CPU 可能
直接使用快取內部的值,而不再重新計算,當然 CPU 內部實際怎麼做也許是難以理解
但是從測試結果表明,x86 CPU 並不是一種穩定的處理器,也許這個演算法可以拿到
別的平台試試看。
圖 13. 測試結果表明 雖然 x86 CPU 並非穩定的 CPU,但是
Carmack 的方法確實是異常的快,至少都有超過 1.5x 的速度
程式中的那個 Dial Widget 是 Qt 本身就有的 元件,用滾輪轉動 Dial Widget 可以動態的
觀察 speed 的變化,Carmack 的快速反平方根演算法來至少都有 1.5x 以上的速度
證明了為何這個演算法會被稱為
John Carmack's Unusual Fast Inverse Square Root
後記 : 這篇文章需要的材料比較多,主要的時間花在理解演算法的由來以及測試程式的撰寫
還有閱讀一些相關計算 平方根 與 反平方根相關的文獻閱讀,不過總算是寫成了。
補充 : 現在 x86 裡面 SSE 指令集裡面就有 rsqrtss,讀者也可以利用這條指令獲得初始值
這條指令基本上就是 快速反平方根演算法 硬體化版本,一樣可以利用初始值做牛頓法疊代
增進解的精度,讀者有興趣可以自己試試看。
圖 14. 使用 SSE 指令 rsqrtss 計算反平方根,內插組合語言
分別給出了 CL 與 GCC 版本內插語法
讀者自己去測試就會知道,使用 rsqrtss 計算速度上並不會得到甚麼優勢,因為 SSE 指令內部
其實最後也是要使用 x86 內的浮點運算器,但是在語法上就變得很簡單,用 rsqrtss 可以直接
獲得近似解,用近似解做初始值放入牛頓法疊代增加解的精度。
對 x86 硬體結構不瞭解可以參考
Software Optimization Guide for the AMD64 Processors
Appendix A Microarchitecture for AMD Athlon 64 and AMD Opteron Processors
對 GCC 內插組合語言語法不熟又懶得看英文,可以參考
Linux Device Driver Programming 驅動程式設計 7-8 行內組譯