高级的算法——倍增!!!
根据LCA的定义,我们可以知道假如有两个节点x和y,则LCA(x,y)是 x 到根的路 径与 y 到根的路径的交汇点,同时也是 x 和 y 之间所有路径中深度最小的节 点,所以,我们可以用遍历路径的方法求 LCA。
但想想都知道啦,这种遍历的方法肯定too slow,最坏情况时可达到O(n),数据大点儿,就光荣TLE了。
所以我们高级的化身——倍增算法就出现了!
谈谈倍增——
倍增简单来讲就是两个点跳到同一高度后,再一起往上跳,直到跳到一个共同的点,就能找到它们的最近公共祖先啦
具体来说,分为以下几个步骤——
首先,我们得找几个帮手——
| 数组 | 解释 |
| f[][] | 预处理倍增f[v][i] |
| d[][] | 记录节点深度 |
| vis[][] | 判重,以防搜到节点的爸爸 |
| head[][] | 存图时用der~(不懂戳) |
| dis[][] |
一个节点到根的最短距离 (有权值记得加权值) |
Step1: 预处理每个结点的深度和该节点的父亲节点
我们用 d 数组来表示每个结点的深度,设节点 1 为根,d[1]=0,初始化 f[v][0]=u, 表示 v 的 20 的祖先节点为 u。
tips:如果树是无根树时需要把它变成有根数(随便找个点就OK)
Step2: 预处理倍增f[v][i],2j 的祖先也是该点 2j-1 祖先的祖先
核心: f[u][j] = f [f [u][j-1]][j-1]
不懂的盆友,我们来举个例子——

我们有这样的一张图,我们对它进行预处理就会变成这样——

*图源戳
还不懂的,就手动模拟一波~
Step3: 查询时,深度大的先往上跳,直至与深度小的点再同一层。若此时两节点相同直接返回此节点(在同一条链上),如果不同,就利用倍增的思想,同时让 x 和 y 向上找,直到找到深度相等且最小的 x 和 y 的祖先 x′,y′,满足 x′≠y′。此时他们的父结点即为 x 和 y 的最近公共祖先 LCA。
倍增解法是 LCA 问题的在线解法,整体时间复杂度是 O(VlogV+QlogV),其 中 Q 是总查询次数。
看起来是不是还不错?那我们来看道题吧~
谈谈题目——
Description
给定一棵n个点的树,Q个询问,每次询问点x到点y两点之间的距离。
Input
第一行一个正整数n,表示这棵树有n个节点;接下来n-1行,每行两个整数x,y表示x,y之间有一条连边;然后一个整数Q,表示有Q个询问;接下来Q行每行两个整数x,y表示询问x到y的距离。
对于全部数据,1≤n≤105,1≤x,y≤n。
Output
输出Q行,每行表示每次询问的答案。
Example
stdin
6
1 2
1 3
2 4
2 5
3 6
2
2 6
5 6
stdout
3
4
*原题戳
Thinking
说实话这题没什么好讲的叭,就是求LCA就OK啦,板子题耶!
上代码——
1 #include<bits/stdc++.h> 2 using namespace std; 3 int t,q,tot; 4 int dis[1100010]; 5 int vis[1100010]; 6 struct node{ 7 int nxt,to; 8 }e[1100010]; 9 int head[1100010]; 10 int f[1100010][20]; 11 int d[1100010]; 12 13 void add(int u, int v){ 14 e[++tot].to = v; 15 e[tot].nxt=head[u]; 16 head[u] = tot; 17 } 18 19 void dfs(int u, int fa, int dep){ //预处理深度,倍增数组 20 vis[u] = 1; 21 f[u][0] = fa; //初始化记录父节点 22 d[u] = dep; 23 for(int j = 1; j <= 19; j++) f[u][j] = f[f[u][j-1]][j-1]; 24 for(int i = head[u]; i; i = e[i].nxt){ 25 int v = e[i].to; 26 if(vis[v]) continue; 27 dfs(v,u,dep+1); 28 } 29 } 30 31 int lca(int x, int y){ //倍增求 LCA 32 if(d[x] > d[y]) swap(x,y); 33 for(int i = 19; i >= 0; i--){ 34 if(d[f[y][i]] >= d[x]) y = f[y][i]; //深度较深节点先往上跳至同一深度 35 if(x == y) return x; 36 } 37 for(int i = 19; i >= 0; i--){ 38 if(f[x][i] != f[y][i]) x = f[x][i], y= f[y][i]; 39 } 40 return f[x][0]; 41 } 42 43 int main(){ 44 scanf("%d",&t); 45 tot = 0; 46 for(int i = 1; i < t; i++){ 47 int u,v; 48 scanf("%d%d",&u,&v); 49 add(u,v),add(v,u); 50 } 51 dfs(1,0,0); 52 cin >> q; 53 for(int i = 1; i <= q; i++){ 54 int x,y; 55 scanf("%d%d",&x,&y); 56 printf("%d ",d[x]+d[y]-2*d[lca(x,y)]); //两个节点到跟的距离减去重复计算的它们公共祖先到跟的距离 57 } 58 }
解释一下这个东西 d[x] + d[y] - 2 * d[lca(x,y)];
画张图——
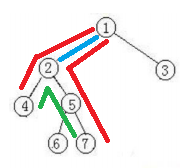
d[x] 和 d[y] 就是红色那两条东西
d[lca(x,y)] 就是蓝色那条
d[x] + d[y] - 2*d[lca(x,y)] 就是绿色那条啦~
当然这是没有权值得时候,我们默认深度差不多等于距离,但有了权值就不一样了。
我们再来看一道板子题——
Description
给出n个点的一棵树,多次询问两点之间的最短距离。
注意:边是双向的。
Input
第一行为两个整数n和m。n表示点数,m表示询问次数; 下来n-1行,每行三个整数x,y,k,表示点x和点y之间存在一条边长度为k;在接下来m行,每行两个整数x,y,表示询问点x到点y的最短距离。
对于全部数据,2≤n≤104,1≤m≤2×104,0<k≤100,1≤x,y≤n。
Output
输出m行。对于每次询问,输出一行。
Example
stdin1
2 2 1 2 100 1 2 2 1
stdout1
100 100
stdin2
3 2 1 2 10 3 1 15 1 2 3 2
stdout2
10 25
*原题戳
1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,m,q,tot; 4 int dis[1100010]; 5 int vis[1100010]; 6 struct node{ 7 int nxt,to; 8 int w; 9 }e[1100010]; 10 int head[1100010]; 11 int f[1100010][20]; 12 int d[1100010]; 13 14 void add(int u, int v, int w){ 15 e[++tot].to = v; 16 e[tot].w = w; 17 e[tot].nxt=head[u]; 18 head[u] = tot; 19 } 20 21 void dfs(int u, int fa, int dep){ 22 vis[u] = 1; 23 f[u][0] = fa; 24 d[u] = dep; 25 for(int j = 1; j <= 19; j++) f[u][j] = f[f[u][j-1]][j-1]; 26 for(int i = head[u]; i; i = e[i].nxt){ 27 int v = e[i].to; 28 if(vis[v]) continue; 29 dis[v] = dis[u] + e[i].w; 30 dfs(v,u,dep+1); 31 } 32 } 33 34 int lca(int x, int y){ 35 if(d[x] > d[y]) swap(x,y); 36 for(int i = 19; i >= 0; i--){ 37 if(d[f[y][i]] >= d[x]) y = f[y][i]; 38 if(x == y) return x; 39 } 40 for(int i = 19; i >= 0; i--){ 41 if(f[x][i] != f[y][i]) x = f[x][i], y= f[y][i]; 42 } 43 return f[x][0]; 44 } 45 int main(){ 46 scanf("%d%d",&n,&m); 47 for(int i = 1; i < n; i++){ 48 int u,v,w; 49 scanf("%d%d%d",&u,&v,&w); 50 add(u,v,w); 51 add(v,u,w); 52 } 53 dfs(1,0,1); 54 for(int i = 1; i <= m; i++){ 55 int x,y; 56 scanf("%d%d",&x,&y); 57 printf("%d ",dis[x]+dis[y]-2*dis[lca(x,y)]); 58 } 59 }
注意到没有?
这一道题是有权值的,所以最后输出的时候输出的是 dis[x] + dis[y] - 2 * dis[lca(x,y)]
总结一下
其实LCA还有别的不同的求法,下次在和你们讲吧(其实是我还没学会)
这次就先到这儿吧~
拜拜~
(如果文章有不对的地方,请指出,谢谢啦^=^)