最大流

1.FF算法

最大流的Ford–Fulkerson 算法基本思想就是增广，直到没有路可以增广为止。
（就是寻找从s到t的整条增广路径，然后增广的一个过程）
如果找不到增广路径，此时的流量就是最大流。

增广路径：定义一条从S至T的道路P。其中一条路径<i,j>

若fij = Cij，称<vi, vj>为饱和弧；否则称<vi, vj>为非饱和弧。
若fij = 0，称<vi, vj>为零流弧；否则称<vi, vj>为非零流弧。
把P 上所有与P 方向一致的弧定义为正向弧，正向弧的全体记为P+；
把P 上所有与P 方向相悖的弧定义为反向弧，反向弧的全体记为P-。
如果满足： fij 是非饱和流，并且<i,j>∈ P+ 或fij 是非零流，并且<i,j>∈ P-
那么就称P 是f 的一条增广路径。

找到增广路径后，就开始增广。找增广路径的同时计算θ。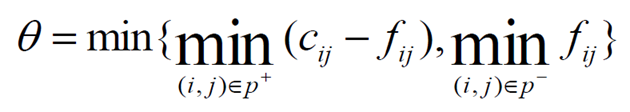

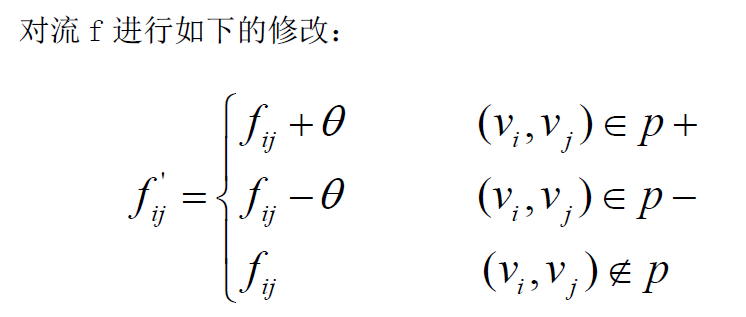
接着，重新进入寻找增广路径的过程。

 

#include<iostream> 
#include<cstdio> 
#include<vector> 
#include<cstring> 
using namespace std; 
struct edge{ 
    int to,rl,ll,fxb; 
}; 
int n;const int INF=1000000000; 
int x=1;
vector<edge> g[8101]; 
bool used[8101];int ans=0;
int a[100001],b[100001];
int _used[100001],_to[100001],h[4001][4001];
int dfs(int u,int t,int f) 
{ 
    if(u==t)return f; 
    used[u]=1; 
    for(int i=0;i<g[u].size();i++) 
    { 
        edge &e=g[u][i]; 
        if(!used[e.to]&&e.rl>e.ll) 
        { 
            f=min(f,e.rl-e.ll); 
            int d=dfs(e.to,t,f); 
            if(d>0) 
            { 
                e.ll+=d; 
                g[e.to][e.fxb].ll-=d; 
                return d; 
            } 
        } 
    } 
    return 0; 
} 
int flow(int s,int t) 
{ 
    int ff=0; 
    for(;;) 
    { 
        memset(used,0,sizeof(used)); 
        int dd=dfs(s,t,INF); 
        if(dd==0)return ff; 
        ff+=dd; 
    } 
} 

dinic：

分层图,以从源点到某点的最短距离分层的图,距离相等的为一层
1.根据残量网络计算分层图（BFS）。
2.在分层图中使用DFS进行增广直到不存在增广路。
3.重复以上步骤直到无法增广。

当前弧优化+多路增广

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
const int INF=1999999999;
int r,c,d;
int n,m;//点，边
struct data {
    int next,to,cap;
} g[200000];
int iter[1000],h[1000],level[1000],k=1,head,tail,q[1000];
void add(int from,int to,int cap) {
    g[++k].next=h[from];
    h[from]=k;
    g[k].to=to;
    g[k].cap=cap;
    g[++k].next=h[to];
    h[to]=k;
    g[k].to=from;
    g[k].cap=0;
}
void bfs(int s) {
    memset(level,0,sizeof(level));
    head=tail=0;
    q[tail++]=s;
    level[s]=1;
    while(head!=tail) {
        int u=q[head++];
        for(int i=h[u]; i; i=g[i].next) {
            if(!level[g[i].to]&&g[i].cap) {
                level[g[i].to]=level[u]+1;
                q[tail++]=g[i].to;
            }
        }
    }
}
int dfs(int u,int t,int f) {
    if(u==t)return f;
    int used=0,w;
    for(int &i=iter[u]; i; i=g[i].next) {
        if(g[i].cap&&level[g[i].to]==level[u]+1) {
            w=f-used;
            w=dfs(g[i].to,t,min(w,g[i].cap));
            if(w) {
                g[i].cap-=w;
                g[i^1].cap+=w;
                used+=w;
                if(used==f)return f;
            }
        }
    }
    return used;
}
int dinic(int s,int t) {
    int flow=0;
    for(;;) {
        for(int i=1; i<=n; i++)iter[i]=h[i];
        bfs(s);
        if(!level[t])return flow;
        flow+=dfs(s,t,INF);
    }
}

下面给出一些网络流的结论与定义

匹配：在图论中，匹配是一个边的集合，其中任意两条边都没有公共顶点。
最大匹配：一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。
完美匹配：如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。
二分图最大匹配=最小点覆盖集=N-最大独立点集
覆盖集：对于每条边，至少选一个端点。
独立集：对于每条边，至多选一个端点。
二分图最大匹配=N-最小路径覆盖
最小路径覆盖：每个节点恰好仅被覆盖一次。
最小链覆盖=最长反链
最小链覆盖：给定N个点的有向无环图，求路径数最少的覆盖，使得每个节点至少被覆盖一次。
用最小路径覆盖求最小链覆盖：从每个点到它能连通的点都连边，这样就转化为最小路径覆盖啦！
反链：对于有向图上不能连通的点建边形成反图，反图上的链叫做反链。