什么是差分约束系统?
差分约束系统是一种特殊的(N)元一次不等式组,它包含(N)个变量(x_1 dots x_N)以及(M)个约束条件,每个约束条件都是由两个变量作差构成的,形如(x_i-x_jle c_k),其中(c_k)是常数,(1le i, jle N, 1le k le M)。我们要解决的问题是:求一组解(x_1=a_1, x_2=a_2, dots, x_N=a_N),使所有约束条件都得到满足。
求解方法
一句话:转化为图模型,然后用最短路或最长路求解,计算最长路和最短路是一样的,就是大、小于号换一下方向就行。
- 约束条件(x_i-x_jle c_k)可以变形为(x_ile x_j+c_k),这与单元最短路径问题中的三角不等式(松弛操作)(dis[y]le dis[x]+z)非常相似,我们可以把这个约束条件转化为一条从(j)到(x)长度为(c_k)的边,简单地说,可以用(j)点松弛(i)点。我们对这个图计算所有点的最短路,就得到了满足一系列约束条件的最小值。
- 约束条件(x_i-x_jge c_k)可以变形为(x_ige x_j+c_k),这与单元最短路径问题中的三角不等式(绷紧操作)(dis[y]ge dis[x]+z)非常相似,我们可以把这个约束条件转化为一条从(j)到(i)长度为(c_k)的边,简单地说,可以用(j)点绷紧(i)点。我们对这个图计算所有点的最长路,就得到了满足一些列约束条件的最大值。
举例说明1:
-
b比a多最少2颗糖,c比b多最少3颗糖,c比a最少多4颗糖,d比c至少多5颗糖
-
转换为公式:$$b-age 2 $$ $$c-bge3 $$ $$c-age 4$$ $$d-cge 5$$
-
公式变形为:$$bge a+2 $$ $$cge b+3$$ $$cge a+4$$ $$dge c+5$$
-
转换为图:
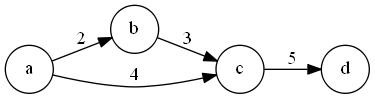
-
这时可以发现,从a到c的最长路才能满足约束条件
-
从a开始计算最长路:
dis[a]=0, dis[b]=2, dis[c]=5, dis[d]=10 -
现在得到的就是满足条件的一组解,而且这是满足约束条件的最小值。
举例说明2:
-
b比a最多多2颗糖,c比b最多多3颗糖,c比a最多多6颗糖,d比c最多多5颗糖
-
转换为公式:$$b-ale 2 $$ $$c-ble3 $$ $$c-ale 6$$ $$d-cle 5$$
-
公式变形为:$$ble a+2 $$ $$cle b+3$$ $$cle a+6$$ $$dle c+5$$
-
转换为图:

-
这时可以发现,从a到c的最短路才能满足约束条件
-
从a开始计算最短路:
dis[a]=0, dis[b]=2, dis[c]=5, dis[d]=10 -
现在得到的就是满足条件的一组解,而且这是满足约束条件的最大值。
解题过程:
- 根据要求规整约束条件,如果要求一组最小值,就全部规整为 (x_i-x_jge c_k) 的形式,然后转化为从(j)到(i)的长为(c_k)的边;如果要求一组最大值,就全部规整为 (x_i-x_jle c_k) 的形式,然后转化为从(j)到(i)的长为(c_k)的边;完成构图。
- 如果只是要判定是否有解,两种形式都可以,但一定是同一种类型。公式是可以按数学方式转换的,如:(a-bge k)可以转换为(b-ale-k)
- 对于“a和b相等”这种条件,可以理解为(a-bge0, b-age0)或(a-ble0, b-ale0),简单说,就是构建两条长为0的双向边。
- 求最小值的话,对图计算最长路;求最大值的话,对图计算最短路。因存在负边,要使用SPFA算法。
- 对于BFS-SPFA和DFS-SPFA,在大多数题中,似乎DFS-SPFA效率更好,如果是判环更是如此。
无解的判定1
-
对于形如 (x_i-x_jle c_k) 的约束系统,求最短路,如果存在负环,则无解
-
如:b比a最多多2颗糖,c比b最多多3颗糖,c比a至少多6颗糖(很明显无解)
-
转换为公式:$$b-ale 2 $$ $$c-ble3 $$ $$c-age 6$$
-
公式变形为:$$ble a+2 $$ $$cle b+3$$ $$ale c-6$$
-
转换为图:
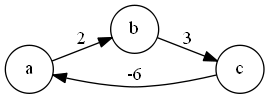
-
可见,图中有负环,无解
无解的判定2
-
对于形如 (x_i-x_jge c_k) 的约束系统,求最长路,如果存在正环,则无解
-
如:b比a多最少2颗糖,c比b多最少3颗糖,c比a最多多4颗糖(很明显无解)
-
转换为公式:$$b-age 2 $$ $$c-bge3 $$ $$c-ale 4$$
-
公式变形为:$$bge a+2 $$ $$cge b+3$$ $$age c-4$$
-
转换为图:
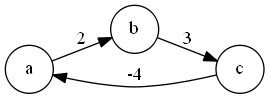
-
可见,图中有正环,无解
关于解的数量
如果(x_1, x_2, dots, x_n)是一组解,很显然(x_1+k, x_2+k, dots, x_3+k)也是一组解,因此在没有特别限定的情况下,差分约束系统要么无解,要么就有无穷多的解。
处理非连通图:
通过差分约束方程构建的图可能是不连通的,你可以从每个点开始一轮SPFA,如:
for(int i=1; i<=N; i++)
if(!vis[i]) SPFA(i);
另一种更常见的作法是构建一个超级点,让这个点连到图上的所有点,然后从超级点开始SPFA。
for(int i=N; i>=1; i--)
add_edge(N+1, i, LEN);
SPFA(N+1);
//N+1号点是超级点
//为什么从N循环到1呢?自己做题就会发现问题。
//LEN是统一的边长,设置的值可以为0,1或-1,取决于dis数组的初始值以及你是松弛操作还是“绷紧”操作
//“绷紧”这个词是我自己发明的。
这个超级结点会破坏原来的约束性吗?不会!因为超级结点(x_0)的含义是这样的:
(x_1-x0ge LEN, x_2-x0ge LEN, x_3-x0ge LEN, dots, x_n-x0ge LEN)
或者
(x_1-x0le LEN, x_2-x0le LEN, x_3-x0le LEN, dots, x_n-x0le LEN)
很显然,超级结点的工作就只是把大家连起来就行了。最后提醒,要想让松弛和绷紧操作启动,LEN值一定要合理设置!
下面是两个模板题的代码。
洛谷P1993小K的农场BFS-SPFA版
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int maxn=10010, maxm=10010;
struct edge{int t, w; edge *nxt; edge(int to, int val, edge *next){t=to, w=val, nxt=next;} };
edge *h[maxn];
void add(int u, int v, int w){ h[u]=new edge(v, w, h[u]); }
int n, m, flag, dis[maxn], instack[maxn]; //flag标记是否有负环
int inq[maxn], cnt[maxn];
bool SPFA(int x)
{
queue<int> Q;
Q.push(x);
inq[x]=1, cnt[x]=1;
while(!Q.empty())
{
int from=Q.front();
Q.pop();
inq[from]=0;
for(edge *p=h[from]; p; p=p->nxt)
{
int to=p->t, w=p->w;
if(dis[to]>dis[from]+w)
{
dis[to]=dis[from]+w;
cnt[to]=cnt[from]+1;
if(cnt[to]>n+1) return false; //false有负环
if(!inq[to])
{
Q.push(to);
inq[to]=1;
}
}
}
}
return true;
}
int main()
{
scanf("%d%d", &n, &m);
for(int i=1, t, a, b, c; i<=m; i++)
{
scanf("%d", &t);
if(t==1) scanf("%d%d%d", &a, &b, &c), add(a, b, -c);
if(t==2) scanf("%d%d%d", &a, &b, &c), add(b, a, c);
if(t==3) scanf("%d%d", &a, &b), add(a, b, 0), add(b, a, 0);
}
for(int i=1; i<=n; i++) add(n+1, i, -1); //加入一个指向所有点的超级结点,使图“联通”起来
//从n+1号点开始,只有负边才能启动松弛,所以,加入的边为-1
flag=SPFA(n+1);
if(flag) printf("Yes
");
else printf("No
");
return 0;
}
洛谷P1993小K的农场DFS-SPFA版,在差分约束类问题中,建议使用DFS的SPFA
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn=10010, maxm=10010;
struct edge{int t, w; edge *nxt; edge(int to, int val, edge *next){t=to, w=val, nxt=next;} };
edge *h[maxn];
void add(int u, int v, int w){ h[u]=new edge(v, w, h[u]); }
int n, m, flag, dis[maxn], instack[maxn]; //flag标记是否有负环
void SPFA(int x)
{
instack[x]=1;
for(edge *p=h[x]; p; p=p->nxt)
{
if(dis[p->t]>dis[x]+p->w) //因dis的初始值都是0,只有负边可以启动松弛,这样避免了大量无用的松弛操作
{
if(instack[p->t])
{
flag=true;
return;
}
dis[p->t]=dis[x]+p->w;
SPFA(p->t);
}
}
instack[x]=0;
}
int main()
{
scanf("%d%d", &n, &m);
for(int i=1, t, a, b, c; i<=m; i++)
{
scanf("%d", &t);
if(t==1) scanf("%d%d%d", &a, &b, &c), add(a, b, -c);
if(t==2) scanf("%d%d%d", &a, &b, &c), add(b, a, c);
if(t==3) scanf("%d%d", &a, &b), add(a, b, 0), add(b, a, 0);
}
for(int i=1; i<=n; i++) add(n+1, i, -1); //加入一个指向所有点的超级结点,使图“联通”起来
//从n+1号点开始,只有负边才能启动松弛,所以,加入的边为-1
flag=false;
dis[n+1]=0;
SPFA(n+1);
if(flag) printf("No
");
else printf("Yes
");
return 0;
}
洛谷P3275糖果DFS-SPFA版,在差分约束类问题中,建议使用DFS的SPFA
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
using namespace std;
const int maxn=100010;
int N, K, dis[maxn], flag, instack[maxn];
struct edge{ int t, w; edge *nxt; edge(int to, int val, edge *next){ t=to, w=val, nxt=next; }};
edge *h[maxn];
void add(int u, int v, int w){ h[u]=new edge(v, w, h[u]); }
void SPFA(int x)
{
instack[x]=1;
for(edge *p=h[x]; p; p=p->nxt)
{
if(flag) return;
if(dis[p->t]<dis[x]+p->w) //求最长路
{
if(instack[p->t])
{
flag=true;
return;
}
dis[p->t]=dis[x]+p->w;
SPFA(p->t);
}
}
instack[x]=0;
}
int main()
{
scanf("%d%d", &N, &K);
for(int i=1, x, a, b; i<=K; i++)
{
scanf("%d%d%d", &x, &a, &b);
if(x==1) add(b, a, 0), add(a, b, 0);
if(x==2) add(a, b, 1);
if(x==3) add(b, a, 0);
if(x==4) add(b, a, 1);
if(x==5) add(a, b, 0);
}
for(int i=N; i>=1; i--) add(N+1, i, 1); //加边的顺序很重要,会极大影响搜索顺序
SPFA(N+1);
if(flag) printf("-1
");
else
{
long long ans=0; //小心1~100000的数列和是超过int范围的
for(int i=1; i<=N; i++) ans+=dis[i];
printf("%lld
", ans);
}
return 0;
}
洛谷P3275糖果BFS-SPFA版,90分,TLE第6个点
//朴素BFS的SPFA会TLE一个点,SLL和SLF优化是否能过没有尝试,本题使用DFS的SPFA效率最高
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
using namespace std;
const int maxn=100010;
int N, K, dis[maxn], cnt[maxn], inq[maxn];
struct edge{ int t, w; edge *nxt; edge(int to, int val, edge *next){ t=to, w=val, nxt=next; }};
edge *h[maxn];
void add(int u, int v, int w){ h[u]=new edge(v, w, h[u]); }
bool SPFA(int x)
{
queue<int> q;
q.push(x);
inq[x]=cnt[x]=1;
while(!q.empty())
{
int from=q.front();
q.pop();
inq[from]=0;
for(edge *p=h[from]; p; p=p->nxt)
{
int to=p->t, w=p->w;
if(dis[to]<dis[from]+w) //求最长路
{
cnt[to]=cnt[from]+1;
if(cnt[to]>N+1) return false;
dis[to]=dis[from]+w;
if(!inq[to])
{
q.push(to);
inq[to]=1;
}
}
}
}
return true;
}
int main()
{
scanf("%d%d", &N, &K);
for(int i=1, x, a, b; i<=K; i++)
{
scanf("%d%d%d", &x, &a, &b);
if(x==1) add(b, a, 0), add(a, b, 0);
if(x==2) add(a, b, 1);
if(x==3) add(b, a, 0);
if(x==4) add(b, a, 1);
if(x==5) add(a, b, 0);
}
for(int i=N; i>=1; i--) add(N+1, i, 1); //加边的顺序很重要,会极大影响搜索顺序
if(!SPFA(N+1)) printf("-1
");
else
{
long long ans=0; //小心1~100000的数列和是超过int范围的
for(int i=1; i<=N; i++) ans+=dis[i];
printf("%lld
", ans);
}
return 0;
}