想象你的麦克风在录制一段由四个纯音同时播放的音频时,由于其只能捕捉强度——时间图像,因此最后的结果看起来相当复杂:

如果给定这样一段音频,该如何将其分解为不同纯音的叠加?
首先考虑只有一个频率的信号,将这个图像缠绕在一个圆上,即想象一个转动的向量,在任意时刻该向量的长度都等于这个时刻的图像高度。由于向量的转动速度可以人为选取,因此这里存在两个频率:信号的频率和缠绕的频率,而缠绕频率可以决定缠绕图像的样子:
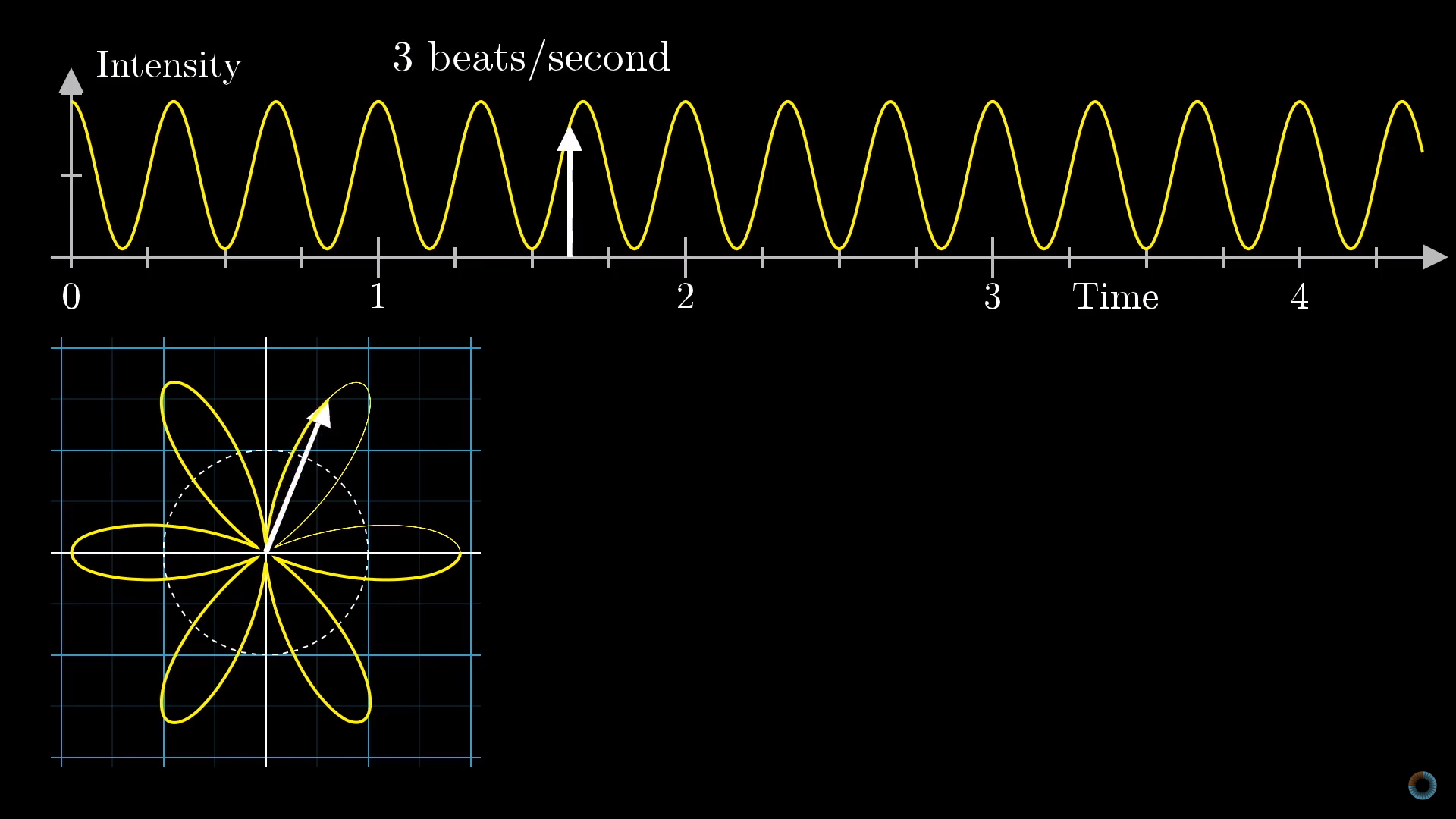
自然地,我们可以想到,当缠绕频率与信号频率相等时,会出现特殊情况。所有高处的点恰好落在圆右侧,而低处的点落在圆左侧:

如何利用这个特性进行定量的分析呢?一个好的方法是计算缠绕图像的质心,为了方便起见,我们仅计算质心的$x$坐标。对大部分的缠绕频率来说,图像的峰和谷会均匀的分布在圆上,导致质心在原点附近;当缠绕频率等于信号频率时,质心会极度偏向右半部分。如果画出质心的$x$坐标相对于缠绕频率的图像,则图像在缠绕频率和信号频率相等处会出现尖峰。我们将这一变换称为近傅里叶变换(Almost-Fourier transform)。
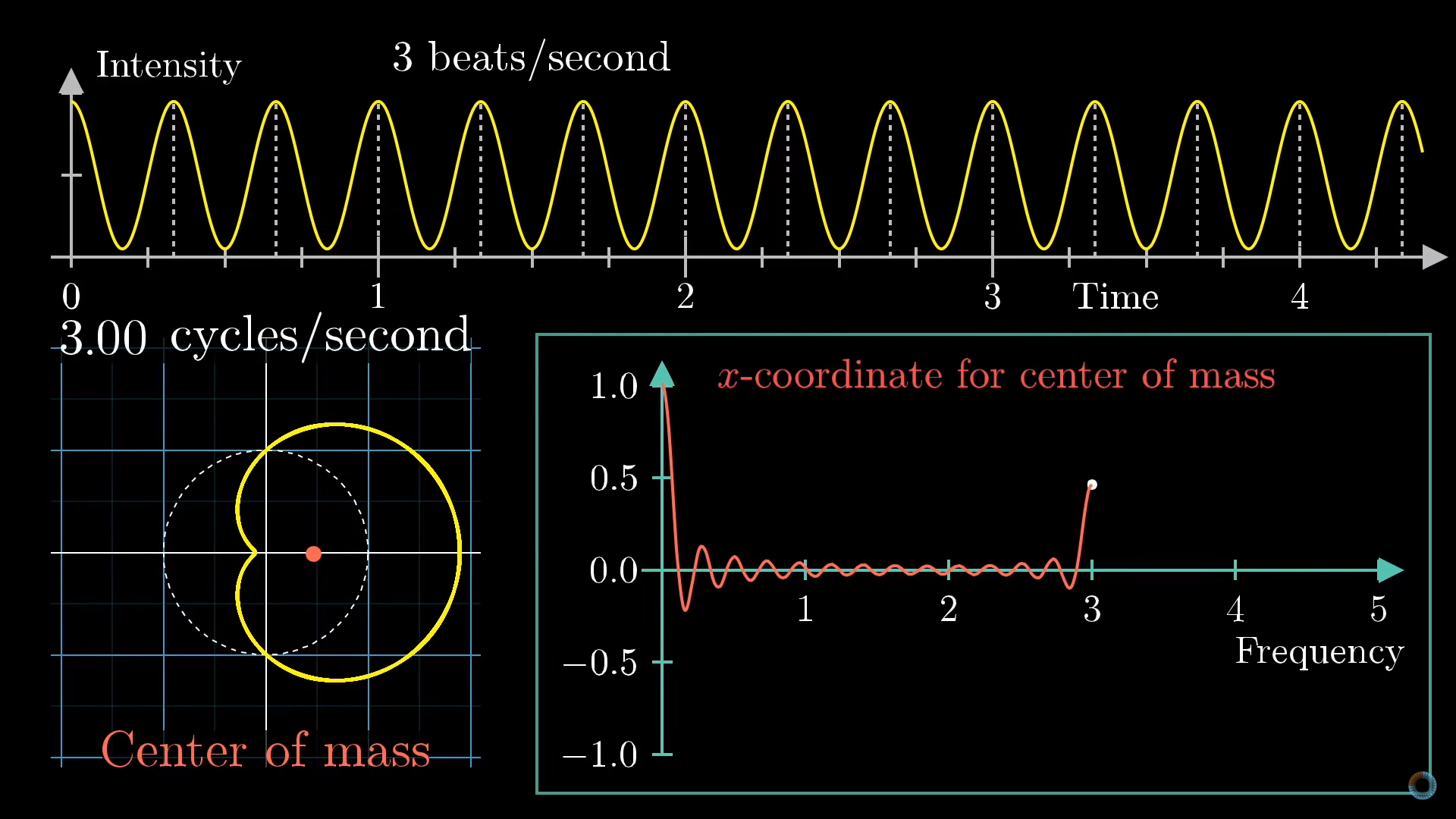
这一方法的真正威力在于它能分离包含多个频率的信号,下图是将一个2Hz + 3Hz的信号进行傅里叶变换的过程:

出现两个尖峰的原因是如果对两个信号分别进行近傅里叶变换之后累加,得到的结果与先将两个结果进行累加再进行近傅里叶变换一致。如果记对信号进行近傅里叶变换为$F(x)$,则有:
$$F(x+y) = F(x) + F(y)$$
为了将质心的$y$坐标也考虑进来,我们引入复平面。则将一个函数$g(t)$以频率为$f$匀速绕原点顺时针缠绕的图像可写作$g(t)e^{-2pi ift}$,为了计算质心,需进行积分:$frac{1}{t_2-t_1}int_{t_1}^{t_2} g(t)e^{-2pi ift} dt$。
真正的傅里叶变换会考虑持续时间的影响,并在整个区间积分,于是上式变为:
$$hat{g}(f) = int_{-infty}^{+infty} g(t)e^{-2pi ift} dt$$
参考链接: