这是我决定开始写博客的第一篇技术博客。整理自己的学习过程,和大家分享,共同进步。
利用这篇博客,我试图把最大似然(估计)以及朴素贝叶斯分类等做个总结,错漏请指正。
1.贝叶斯公式
贝叶斯公式作为概率论中的基础,大家都见过,极为简单。但是学习时候无非用于一些红球黑球,男生女生的估计问题,学起来也是兴趣寥寥。我也不曾想它用处之大,可谓大道至简。
如果对于概率还没有基础或者兴趣的人,先看看刘未鹏大牛的入门博客:《数学之美番外篇:平凡而又神奇的贝叶斯方法》。文章中对于贝叶斯方法的描述和逻辑上的讲解非常清楚,所以这里也就不赘述了,没看过的还请先移步看看这篇博客。
首先,援引维基百科对于贝叶斯定理的条件概率推导:

这个公式就是贝叶斯公式,也很好理解,重点在于,在碰到问题时,如何能够将实际问题与之联系起来,也就是从实际问题到数学模型的转换过程。比如我当年看到这个公式,是万万不能想到它可以用在包括分类和输入预测这么宽泛的地方。
2.朴素贝叶斯分类
在贝叶斯公式中的A和B,我们习惯于称之为事件A,事件B.但是事实上,这个A,B我们可以拓展为类别,观测量这样更好理解。以机器学习的朴素贝叶斯分类为例,假如我获得一组观测量(特征)F={f1 ,f2,,,fn},想判断该组特征属于k个类别中的某一类C={c1 ,c2,,,ck}.(如果是垃圾邮件分类中则只有两类,垃圾邮件或者非垃圾邮件)。
那么简单来讲,如果我们获得在这组特征的情况下的各个类别的概率Pi=P(ci|F), 则最大概率的那个类别即为这组特征的分类估计。那么根据贝叶斯公式
P(ci|F)=P(F|ci)*P(ci)/P(F)
上式中,在计算第i个类别的概率时候分母都是P(F),在分类中只需要最大的不需要具体概率值的时候,我们可以只需要找出分子P(F|ci)*P(ci)最大的那一类。根据训练数据集(已知的数据集),P(ci)也就是每个类别本身发生的概率是可以统计(估计出来),也可能是通过假设各个类别等概率(1/类的数量)来得到,所以关键在于如何获得某个类别下观测特征的条件概率P(F|ci)。
P(F|ci)*P(ci)=P(F,ci)
=P(f1 ,f2,,,fn,ci)
这个时候,朴素贝叶斯的“朴素”就要派上用场了。我们知道,当两个事件统计独立的时候则有
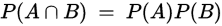
那么朴素贝叶斯的思想则是认为给定样本每个特征与其他特征都不相关,也就是说任何fm与fn无关,则
P(F|ci)*P(ci)=P(F,ci)
=P(f1 ,f2,,,fn,ci)
=P(ci)*P(f1|ci)*P(f2|ci)...*P(fn|ci)
那么在这个朴素假设下,根据最大后验概率MAP, 我们就可以计算出来该组特征的分类:
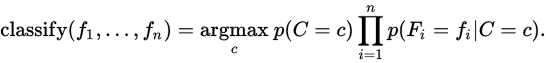
但是,根据数据类型的不同,或者说P(fn|ci)的计算方法不同,可以有三种贝叶斯计算方法。
2.1 高斯朴素贝叶斯
但是如果对于连续数据的处理,也就是特征值可能为连续值,不一定出现在训练集中的情况,我们通常假设连续特征为高斯分布,根据训练集数据求均值和方差获得其高斯分布的概率密度参数。在分类过程中需要求解某个特征值fn的时候,以其对应的高斯密度来代替其概率值。详见
维基百科对于高斯朴素贝叶斯的解释:
2.2 多元朴素贝叶斯
如果是离散的训练数据集,比如垃圾邮件分类问题中。P(fn|ci)的计算是通过计数,即特征fn(在垃圾邮件分类中为每个字)在每个类别(垃圾/非垃圾)中出现的的次数和总字数的比较得出。
值得注意的是,在离散样本也就是基于频率的估计中,如果某个特征fn未在训练集的类别ci中出现过,那么P(fn|ci)项为0会导致整个估计为0而忽略了其他的特征信息。这样的估计显然是不准确的,所以通常需要对于样本进行样本修正保证不会有0概率出现。比如采用laplace校准,对没类别下所有划分的计数加1,这样如果训练样本集数量充分大时,并不会对结果产生影响。listone修正则是加一个0-1之间的数。
2.3 伯努利模型
和多元朴素贝叶斯中通过特征出现频率来计算P(fn|ci)不同,伯努利模型只考虑出现不出现的二值问题。
伯努利模型中,条件概率P(fn|ci)的计算方式是:
当特征值fn为1时,P(fn|ci)=P(fn=1|ci);
当特征值fn为0时,P(fn|ci)=1−P(fn=1|ci);
还是以垃圾邮件分类为例,P(fn|ci)=(类ci下包含单词fn的文件数+1)/(类ci下单词总数+2)
同时也要主要,朴素贝叶斯对于独立性的要求需要认真对数据进行预处理(6 Easy Steps to Learn Naive Bayes Algorithm)。
朴素贝叶斯更多分类具体案例详见维基百科性别分类的例子 和参考5.
当然,刘未鹏在上述提到神奇的贝叶斯方法一文中,关于利用贝叶斯方法进行输入预测的案例也很有趣。总的来说,朴素贝叶斯因为计算快可以用在实时分类预测中,也用于多类别预测、文本分类,垃圾过滤和情绪分析以及推荐系统中。
3.最大似然估计
第2节中提到,最终估计类别时候用到最大后验概率,而在参数估计中还有另一种声音,即是所谓的频率派的最大似然估计。在刘未鹏的文章中有这么一段话:
P(h | D) ∝ P(h) * P(D | h) (注:那个符号的意思是“正比例于”,不是无穷大,注意符号右端是有一个小缺口的。)
这个式子的抽象含义是:对于给定观测数据,一个猜测是好是坏,取决于“这个猜测本身独立的可能性大小(先验概率,Prior )”和“这个猜测生成我们观测到的数据的可能性大小”(似然,Likelihood )的乘积。具体到我们的那个 thew 例子上,含义就是,用户实际是想输入 the 的可能性大小取决于 the 本身在词汇表中被使用的可能性(频繁程度)大小(先验概率)和 想打 the 却打成 thew 的可能性大小(似然)的乘积。
下面的事情就很简单了,对于我们猜测为可能的每个单词计算一下 P(h) * P(D | h) 这个值,然后取最大的,得到的就是最靠谱的猜测。
这里的h相当于我们的c(模型,参数),D相当于上文的F(观测值).这便是典型的贝叶斯派的看法,也就是认为,最好的估计需要同时考虑该模型生成当前特征值的可能性和模型本身先验概率(出现频率)。
而最大似然估计不一样,最大似然估计只考虑 P(D | h),也就是寻找最可能产生当前观测值的模型而不考虑该模型本身的先验概率,当然对于先验概率均等的情况则两者一致。如果对先验概率一无所知,则也只能采取最大似然估计。同样,刘未鹏对于最大似然和贝叶斯估计的例子:
我们通过:
P(h | D) ∝ P(h) * P(D | h)
来比较哪个模型最为靠谱。前面提到,光靠 P(D | h) (即“似然”)是不够的,有时候还需要引入 P(h) 这个先验概率。奥卡姆剃刀就是说 P(h) 较大的模型有较大的优势,而最大似然则是说最符合观测数据的(即 P(D | h) 最大的)最有优势。整个模型比较就是这两方力量的拉锯。我们不妨再举一个简单的例子来说明这一精神:你随便找枚硬币,掷一下,观察一下结果。好,你观察到的结果要么是“正”,要么是“反”(不,不是少林足球那枚硬币:P ),不妨假设你观察到的是“正”。现在你要去根据这个观测数据推断这枚硬币掷出“正”的概率是多大。根据最大似然估计的精神,我们应该猜测这枚硬币掷出“正”的概率是 1 ,因为这个才是能最大化 P(D | h) 的那个猜测。然而每个人都会大摇其头——很显然,你随机摸出一枚硬币这枚硬币居然没有反面的概率是“不存在的”,我们对一枚随机硬币是否一枚有偏硬币,偏了多少,是有着一个先验的认识的,这个认识就是绝大多数硬币都是基本公平的,偏得越多的硬币越少见(可以用一个 beta 分布来表达这一先验概率)。将这个先验正态分布 p(θ) (其中 θ 表示硬币掷出正面的比例,小写的 p 代表这是概率密度函数)结合到我们的问题中,我们便不是去最大化 P(D | h) ,而是去最大化 P(D | θ) * p(θ) ,显然 θ = 1 是不行的,因为 P(θ=1) 为 0 ,导致整个乘积也为 0 。实际上,只要对这个式子求一个导数就可以得到最值点。
以上说的是当我们知道先验概率 P(h) 的时候,光用最大似然是不靠谱的,因为最大似然的猜测可能先验概率非常小。然而,有些时候,我们对于先验概率一无所知,只能假设每种猜测的先验概率是均等的,这个时候就只有用最大似然了。实际上,统计学家和贝叶斯学家有一个有趣的争论,统计学家说:我们让数据自己说话。言下之意就是要摒弃先验概率。而贝叶斯支持者则说:数据会有各种各样的偏差,而一个靠谱的先验概率则可以对这些随机噪音做到健壮。事实证明贝叶斯派胜利了,胜利的关键在于所谓先验概率其实也是经验统计的结果,譬如为什么我们会认为绝大多数硬币是基本公平的?为什么我们认为大多数人的肥胖适中?为什么我们认为肤色是种族相关的,而体重则与种族无关?先验概率里面的“先验”并不是指先于一切经验,而是仅指先于我们“当前”给出的观测数据而已,在硬币的例子中先验指的只是先于我们知道投掷的结果这个经验,而并非“先天”。
援引wiki对似然函数的定义
似然函数:
并且在
的所有取值上通过令一阶导数等于零,使这个函数取到最大值。这个使可能性最大的
值即称为
的最大似然估计。
- 这里的似然函数是指
不变时,关于
的一个函数。
- 最大似然估计函数不一定是惟一的,甚至不一定存在。
参考4博客中的例子,很好的说明了最大似然估计:
假如有一个罐子,里面有黑白两种颜色的球,数目多少不知,两种颜色的比例也不知。我 们想知道罐中白球和黑球的比例,但我们不能把罐中的球全部拿出来数。现在我们可以每次任意从已经摇匀的罐中拿一个球出来,记录球的颜色,然后把拿出来的球 再放回罐中。这个过程可以重复,我们可以用记录的球的颜色来估计罐中黑白球的比例。假如在前面的一百次重复记录中,有七十次是白球,请问罐中白球所占的比例最有可能是多少?很多人马上就有答案了:70%。而其后的理论支撑是什么呢?
我们假设罐中白球的比例是p,那么黑球的比例就是1-p。因为每抽一个球出来,在记录颜色之后,我们把抽出的球放回了罐中并摇匀,所以每次抽出来的球的颜 色服从同一独立分布。这里我们把一次抽出来球的颜色称为一次抽样。题目中在一百次抽样中,七十次是白球的概率是P(Data | M),这里Data是所有的数据,M是所给出的模型,表示每次抽出来的球是白色的概率为p。如果第一抽样的结果记为x1,第二抽样的结果记为x2... 那么Data = (x1,x2,…,x100)。这样,
P(Data | M)
= P(x1,x2,…,x100|M)
= P(x1|M)P(x2|M)…P(x100|M)
= p^70(1-p)^30.
那么p在取什么值的时候,P(Data |M)的值最大呢?将p^70(1-p)^30对p求导,并其等于零。
70p^69(1-p)^30-p^70*30(1-p)^29=0。
解方程可以得到p=0.7。
在边界点p=0,1,P(Data|M)=0。所以当p=0.7时,P(Data|M)的值最大。这和我们常识中按抽样中的比例来计算的结果是一样的。
另外,有兴趣的童鞋,利用Python的Sklearn的naive bayes库可以很方便的实现朴素贝叶斯。
参考:
1.https://zh.wikipedia.org/wiki/%E8%B4%9D%E5%8F%B6%E6%96%AF%E5%AE%9A%E7%90%86
3.https://www.analyticsvidhya.com/blog/2015/09/naive-bayes-explained/
4.http://www.cnblogs.com/liliu/archive/2010/11/22/1883702.html
5.http://www.cnblogs.com/leoo2sk/archive/2010/09/17/naive-bayesian-classifier.html

