设$ heta$是一个未知的参数向量,$J( heta)$是相应的需要被最小化的代价函数。假设函数$J( heta)$是可微的。
这个算法从最小点的初始估计值$ heta(0)$开始,之后的算法按照如下形式迭代:
$$ heta(new) = heta(old)+Delta heta$$
$$Delta heta = -mufrac{partial J( heta)}{partial heta}Bigg|_{ heta = heta(old)}$$
该式中$mugt0$。如果寻找的是最大值,那么该算法被称为梯度上升法,并去掉上式中的负号。
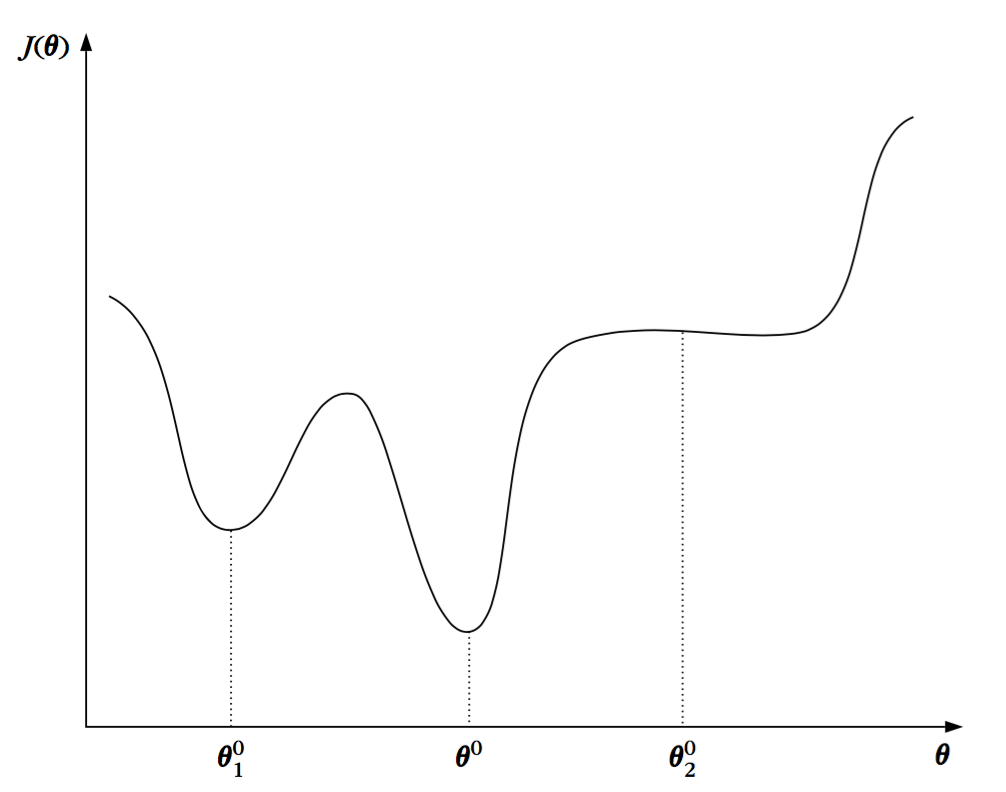
下图展示了该方法的几何解释。新的估计值$ heta(new)$是沿着减小$J( heta)$的方向选取的。参数$mu$是非常重要的,并且在算法的收敛中扮演了重要的角色。如果它很小的话,那么修正值$Delta heta$也很小,并且收敛到最小值点就变得非常缓慢。另一方面,如果它很大的话,那么算法可能会在最优值附近震荡,也不可能收敛。然而,如果这个参数选取合适,那么算法将会收敛到$J( heta)$的一个驻点,该驻点可以是一个局部最小值(${ heta}_1^0$)或者一个全局最小值(${ heta}^0$)或者一个鞍点(${ heta}_2^0$)。
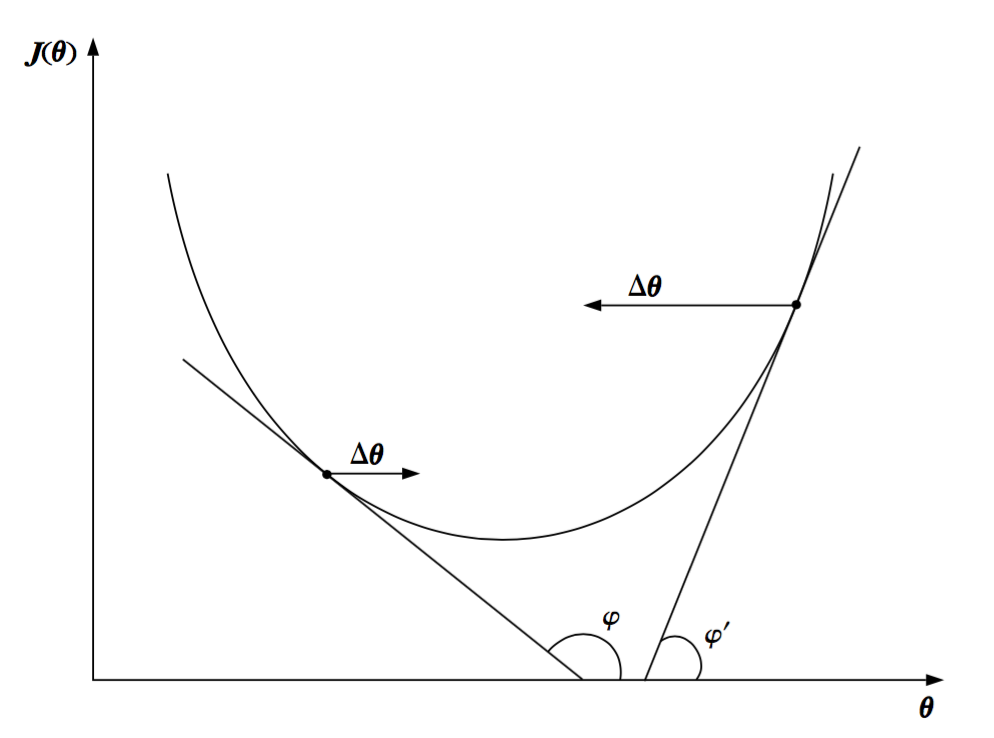
换句话说,它收敛到梯度等于0的一个点,如下图所示。算法将要收敛到哪一个驻点依赖于初始点的位置。此外,收敛的速度依赖于代价函数$J( heta)$的形式。
下图展示了两种情形下不同值c的等高线$J( heta) = c$,维度是二维空间,即$ heta = [ heta_1, heta_2]^T$。最优值$ heta^0$落在等高线的中心,梯度$frac{partial J( heta)}{partial heta}$总是垂直于等值面的切平面。
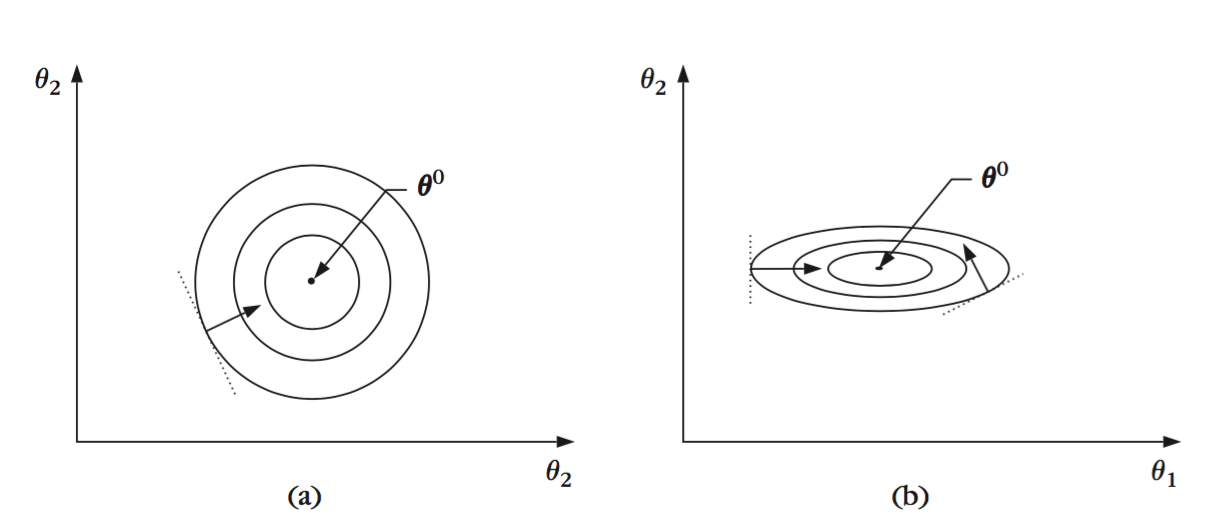
事实上,如果$J( heta) = c$,那么
$${ m d}c = 0 = frac{partial J( heta)^T}{partial heta}{ m d} heta Longrightarrow frac{J( heta)}{partial heta}perp { m d} heta$$