一、CTR中的特征交互
在计算广告和推荐系统中,CTR预估(click-through rate)是非常重要的一个环节,判断一个商品的是否进行推荐需要根据CTR预估的点击率来进行。在进行CTR预估时,除了单特征外,往往要对特征进行组合。
普通的线性模型,我们都是将各个特征独立考虑的,并没有考虑到特征与特征之间的相互关系。但实际上,大量的特征之间是有关联的。最简单的以电商为例,一般女性用户看化妆品服装之类的广告比较多,而男性更青睐各种球类装备。那很明显,女性这个特征与化妆品类服装类商品有很大的关联性,男性这个特征与球类装备的关联性更为密切。如果我们能将这些有关联的特征找出来,显然是很有意义的。
FM,完成了上述特征交互。
二、从线性模型到FM
1、线性模型
一般的线性模型没有考虑特征间的关联。
2、多项式模型
上式中,n表示样本的特征数量,(x_i)表示第(i)个特征的值。注意:一般而言,特征只会和其它特征组合,而不会和自己组合。所以(j)的取值不会和(i)有重叠。组合部分的特征相关参数共有(n(n−1)/2)个
3、多项式模型存在的问题
CTR数据集是数据稀疏的,其稀疏性原因:类别特征需要进行one-hot编码。假设淘宝或者京东上的item为100万,如果对item这个维度进行one-hot编码,光这一个维度数据的稀疏度就是百万分之一。
数据稀疏带来的问题:(w_i)和(w_j)都不为0的情况非常少,这样就导致(w_{ij})无法训练得出。即:没有出现交互的特征组合,不能对对应的参数进行估计。
4、问题解决思路
由3可知,当(x_i)为0,(w_{ij})就无法训练更新,
利用矩阵分解的思路,对二阶交叉特征的系数进行调整,让系数不在是独立无关的,从而减少模型独立系数的数量。
对(x_i)引入一个辅助向量,由隐向量(v_i=(v_{i1},v_{i2},⋯,v_{ik}))来代表(x_i),(k)为隐向量维度。
得到隐向量embedding矩阵(V):
(V)的第(j)行就是第(j)个特征的隐向量。
这样(w_{ij})变为:
为何可以完成上述矩阵分解:
对于任意对称的正定矩阵(W),只要(k)足够大,一定存在一个矩阵(V),使得(W=VV^T)。
首先,(hat{W})的每个元素都是两个向量的内积,所以一定是对称的。
第二,如何保证(hat{W})的正定性:我们只关心互异特征分量之间的相互关系,因此(hat{W})的对角线元素是任意取值的,只需将它们取得足够大(例如保证行元素满足严格对角占优),就可以保证(hat{W})的正定性。
理论上,我们要求参数(k)取得足够大,但是,在高度稀疏的数据场景中,由于没有足够的样本来估计复杂的交互矩阵,因为(k)通常应取得很小。
此时,公式(2)就变为:
其中(<V_i,V_j>)表示两个(k)维向量的点乘:
三、FM公式解析
1、复杂度分析
FM模型公式(3)需要估计的参数包括:
共有(1+n+nk)个。其中,(w_0)为整体的偏置量,(w)对特征向量的各个分量的强度进行建模,(V)对特征向量中任意两个分量之间的关系进行了建模。
其时间复杂度:(O(kn^2))
花括号分别对应二阶项的加法项和乘法项。
2、二阶项公式变换
通过变换降低其时间复杂度。
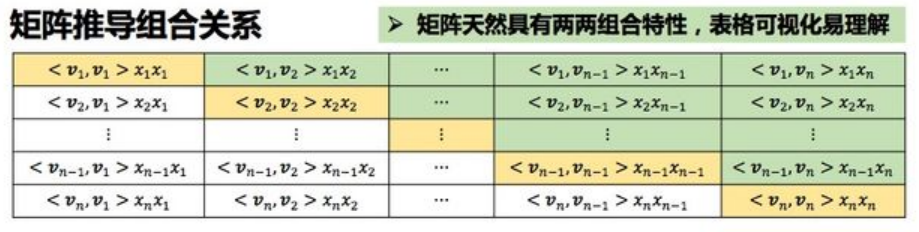
如上图所示,FM二阶项为图中绿色部分。而全图包含了 (2*绿色部分 + 对角线)。
所以:
变换之后的时间复杂度为:(O(kn))。
3、导数和损失函数
经过变换,最终,FM模型公式为:
3.1 导数
对三个参数的导数为:
对(w_0,w)的求导很好理解,对(v_{i,f})的求导,其推导过程:
为何(i)变成了(j),前半部分求和和i无关,换个符号以便区分。
3.2 损失函数
FM用于CTR时,借助于LR,相当于二分类任务,使用交叉熵损失函数。
(hat{y})为FM模型的输出,(hat{h})为加上sigmoid函数之后的模型最终输出。
1、当(h in {0,1}),用于CTR,则交叉熵损失函数为:
2、当 (h in {-1,1}),用于二分类则交叉熵损失函数,等价于Logit loss为:
3.3 随机梯度下降过程的参数更新
以 (h in {-1,1}) 为例,三个参数导数为:
可知,在求梯度过程中,三个参数都有([delta(yhat{y}-1]cdot y)这一公共部分。
参数更新公式:
四、python实现FM二分类
已知模型公式和参数更新公式,如何转换成对应的python代码
1、参数初始化
w_0 = 0.
w = zeros((n, 1)) # 其中n是特征的个数
v = normalvariate(0, 0.2) * ones((n, k)) # embedding矩阵V
2、前项传播:公式转换为矩阵乘法
假设样本矩阵为dataMatrix,其形状为(m*n),表示m个样本,每个样本有n个特征。则 dataMatrix[i] 为第i个样本。
classLabels为标签列表。classLabels[i]为第i个样本的真实label。
一阶项,相乘然后求和,变为矩阵点积。对应点积的地方通常会有sum,对应位置积的地方通常都没有
linear_part = dataMatrix[x] * w
二阶交叉项:第一部分相乘求和,变为矩阵点积。第二部分,先各自完成对应元素相乘,然后矩阵点积。
# xi·vi,xi与vi的矩阵点积
inter_1 = dataMatrix[i] * v # x,int。表示第几个样本的特征向量
# xi与xi的对应位置乘积 与 xi^2与vi^2对应位置的乘积 的点积
inter_2 = multiply(dataMatrix[i], dataMatrix[i]) * multiply(v, v) # multiply对应元素相乘
# 完成交叉项,xi*vi*xi*vi - xi^2*vi^2
interaction = sum(multiply(inter_1, inter_1) - inter_2) / 2.
模型输出:偏置项+一阶+二阶。注意:这里没有sigmoid。
p = w_0 + dataMatrix[x] * w + interaction
3、参数更新
1、计算sigmoid(y*pred_y)-1
tmp = sigmoid(classLabels[x] * p[0, 0]) - 1
为何这里使用p[0,0],因为p的类型为:<class 'numpy.matrix'>,其值形如:[[-0.48939694]]。所以p[0,0]得到具体数值。
2、三个参数的更新规则:随机梯度下降,每个样本x训练完成,进行更新。
w_0 = w_0 + alpha * tmp * classLabels[x]
# 由于w有n个值,每个值迭代更新
for i in range(n):
if dataMatrix[x, i] != 0:
w[i, 0] = w[i, 0] + alpha * tmp * classLabels[x] * dataMatrix[x, i]
for j in range(k): # V的第i行有k个值,也是每个值迭代更新
v[i, j] = v[i, j] + alpha * tmp * classLabels[x] * (dataMatrix[x, i] * inter_1[0, j] - v[i, j] * dataMatrix[x, i] * dataMatrix[x, i])
4、代码完成
1、数据集预处理
皮马人糖尿病数据集:https://github.com/susanli2016/Machine-Learning-with-Python/blob/master/diabetes.csv
进行训练集、测试集切分
import numpy as np
import random
# 数据集切分
def loadData(fileName,ratio): # ratio,训练集与测试集比列
trainingData = []
testData = []
with open(fileName) as txtData:
lines = txtData.readlines()
for line in lines:
lineData = line.strip().split(',')
if random.random() < ratio: #数据集分割比例
trainingData.append(lineData) #训练数据集列表
else:
testData.append(lineData) #测试数据集列表
np.savetxt('./data/diabetes_train.txt', trainingData, delimiter=',',fmt='%s')
np.savetxt('./data/diabetes_test.txt', testData, delimiter=',',fmt='%s')
return trainingData,testData
diabetes_file = './data/diabetes.csv'
trainingData, testData = loadData(diabetes_file,0.8)
2、FM实现
# FM二分类
# diabetes皮马人糖尿病数据集
# coding:UTF-8
from numpy import *
from random import normalvariate # 正态分布
from datetime import datetime
import pandas as pd
import numpy as np
# 处理数据
def preprocessData(data):
feature = np.array(data.iloc[:, :-1]) # 取特征(8个特征)
label = data.iloc[:, -1].map(lambda x: 1 if x == 1 else -1) # 取标签并转化为 +1,-1
# 将数组按行进行归一化
zmax, zmin = feature.max(axis=0), feature.min(axis=0) # 特征的最大值,特征的最小值
feature = (feature - zmin) / (zmax - zmin)
label = np.array(label)
return feature, label
def sigmoid(inx):
return 1.0 / (1 + np.exp(-inx))
# 训练FM模型
def FM(dataMatrix, classLabels, k, iter, alpha):
'''
:param dataMatrix: 特征矩阵
:param classLabels: 标签矩阵
:param k: v的维数
:param iter: 迭代次数
:return: 常数项w_0, 一阶特征系数w, 二阶交叉特征系数v
'''
# dataMatrix用的是matrix, classLabels是列表
m, n = shape(dataMatrix) # 矩阵的行列数,即样本数m和特征数n
# 初始化参数
w = zeros((n, 1)) # 一阶特征的系数
w_0 = 0 # 常数项
v = normalvariate(0, 0.2) * ones((n, k)) # 即生成辅助向量(n*k),用来训练二阶交叉特征的系数
for it in range(iter):
for x in range(m): # 随机优化,每次只使用一个样本
# 二阶项的计算
inter_1 = dataMatrix[x] * v # 每个样本(1*n)x(n*k),得到k维向量(FM化简公式大括号内的第一项)
inter_2 = multiply(dataMatrix[x], dataMatrix[x]) * multiply(v, v) # 二阶交叉项计算,得到k维向量(FM化简公式大括号内的第二项)
interaction = sum(multiply(inter_1, inter_1) - inter_2) / 2. # 二阶交叉项计算完成(FM化简公式的大括号外累加)
p = w_0 + dataMatrix[x] * w + interaction # 计算预测的输出,即FM的全部项之和
tmp = 1 - sigmoid(classLabels[x] * p[0, 0]) # tmp迭代公式的中间变量,便于计算
w_0 = w_0 + alpha * tmp * classLabels[x]
for i in range(n):
if dataMatrix[x, i] != 0:
w[i, 0] = w[i, 0] + alpha * tmp * classLabels[x] * dataMatrix[x, i]
for j in range(k):
v[i, j] = v[i, j] + alpha * tmp * classLabels[x] * (
dataMatrix[x, i] * inter_1[0, j] - v[i, j] * dataMatrix[x, i] * dataMatrix[x, i])
# 计算损失函数的值
if it % 10 == 0:
loss = getLoss(getPrediction(mat(dataMatrix), w_0, w, v), classLabels)
print("第{}次迭代后的损失为{}".format(it, loss))
return w_0, w, v
# 损失函数
def getLoss(predict, classLabels):
m = len(predict)
loss = 0.0
for i in range(m):
loss -= log(sigmoid(predict[i] * classLabels[i]))
return loss
# 预测
def getPrediction(dataMatrix, w_0, w, v):
m = np.shape(dataMatrix)[0]
result = []
for x in range(m):
inter_1 = dataMatrix[x] * v
inter_2 = multiply(dataMatrix[x], dataMatrix[x]) * multiply(v, v) # multiply对应元素相乘
# 完成交叉项
interaction = np.sum(multiply(inter_1, inter_1) - inter_2) / 2.
p = w_0 + dataMatrix[x] * w + interaction # 计算预测的输出
pre = sigmoid(p[0, 0])
result.append(pre)
return result
# 评估预测的准确性
def getAccuracy(predict, classLabels):
m = len(predict)
allItem = 0
error = 0
for i in range(m): # 计算每一个样本的误差
allItem += 1
if float(predict[i]) < 0.5 and classLabels[i] == 1.0:
error += 1
elif float(predict[i]) >= 0.5 and classLabels[i] == -1.0:
error += 1
else:
continue
return float(error) / allItem
if __name__ == '__main__':
trainData = './data/diabetes_train.txt'
testData = './data/diabetes_test.txt'
train = pd.read_csv(trainData)
test = pd.read_csv(testData)
dataTrain, labelTrain = preprocessData(train)
dataTest, labelTest = preprocessData(test)
date_startTrain = datetime.now()
print("开始训练")
w_0, w, v = FM(mat(dataTrain), labelTrain, 4, 100, 0.01)
print("w_0:", w_0)
print("w:", w)
print("v:", v)
predict_train_result = getPrediction(mat(dataTrain), w_0, w, v) # 得到训练的准确性
print("训练准确性为:%f" % (1 - getAccuracy(predict_train_result, labelTrain)))
date_endTrain = datetime.now()
print("训练用时为:%s" % (date_endTrain - date_startTrain))
print("开始测试")
predict_test_result = getPrediction(mat(dataTest), w_0, w, v) # 得到测试的准确性
print("测试准确性为:%f" % (1 - getAccuracy(predict_test_result, labelTest)))
python版fm代码解析:
1、损失函数,输入m个样本,损失函数累加。
2、预测时候的输出使用了sigmoid。这样是FM模型和sigmoid进行了分割,分为了两个阶段,因为如前面所说,在参数更新过程中,使用了logit loss作为损失函数,而这个损失函数的输入为sigmoid之前的fm模型的原始输出。但是到了准确率评估阶段,需要将fm模型的原始输出经过sigmoid,这样就可以以0.5为阈值,进行正负例区分。
3、预测准确率:预测值大于0.5为正例,小于0.5为负例。
ps: 公式到代码的转换:累加和变矩阵乘法,试想,矩阵乘法里就是一行*一列,然后累加和。
参考文献
1、FM因子分解机的原理、公式推导、Python实现和应用
2、FM算法解析及Python实现
3、分解机(Factorization Machines)推荐算法原理
4、深度学习遇上推荐系统(一)--FM模型理论和实践