19.11.4总结
估分:100+70+63
实际:100+0+63
T1

原题。
先把障碍点排序,保证后面的点不能走到前面的点。
设f[i]表示从原点开始走,不经过其他障碍点到达障碍点i的方案数。
求f[i]的时候,用全部方案减去不合法的方案。
显然,某一种不合法的方案有且仅有一个"最先经过的障碍点"
所以O((m^2))转移就好了。
T2

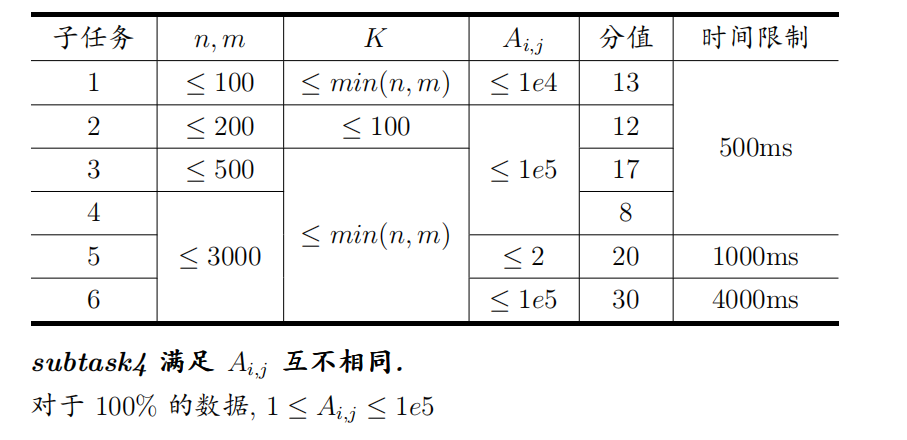
O(nmK)做法显然
正解
考虑扫描线,一次求出一行的f。
当我们加入一个点时,它会对一个正方形区域造成影响。然而,由于相同颜色的点贡献不能重复计算,所以实际它影响的是一个区间。如下图,只用把蓝色部分的答案++就好了。维护一个差分数组。

删除的情况也类似。
现在我们需要一个能支持插入,删除,查找前驱后继的数据结构。
给每一个点开一个bitset。
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<bitset>
using namespace std;
long long n,m,i,j,k,ans1,ans2,S,bzz;
int sum[3][3005][3005];
int a[3005][3005];
long long delta[3005],f[3005];
bitset<3105> B1[100005],B2[100005];
int g[3005][3005],last[100005];
void does2()
{
for (i=1;i<=n;i++)
for (j=1;j<=m;j++)
{
sum[1][i][j]=sum[1][i-1][j]+sum[1][i][j-1]-sum[1][i-1][j-1]+(a[i][j]==1);
sum[2][i][j]=sum[2][i-1][j]+sum[2][i][j-1]-sum[2][i-1][j-1]+(a[i][j]==2);
}
for (i=1;i<=n-k+1;i++)
{
for (j=1;j<=m-k+1;j++)
{
S=0;
if (sum[1][i+k-1][j+k-1]-sum[1][i-1][j+k-1]-sum[1][i+k-1][j-1]+sum[1][i-1][j-1]>0) S++;
if (sum[2][i+k-1][j+k-1]-sum[2][i-1][j+k-1]-sum[2][i+k-1][j-1]+sum[2][i-1][j-1]>0) S++;
ans1=max(ans1,S);
ans2=ans2+S;
}
}
printf("%lld %lld",ans1,ans2);
}
void getg()
{
for (i=1;i<=100000;i++) last[i]=n+k+1;
for (j=1;j<=m;j++)
{
for (i=n;i>=1;i--)
g[i][j]=(last[a[i][j]]-i<k),last[a[i][j]]=i;
for (i=n;i>=1;i--)
last[a[i][j]]=n+k+1;
}
}
void ADD(long long x,long long y)
{
long long Pre,Nex;
if (B2[a[x][y]][y]) return;
Pre=m-B1[a[x][y]]._Find_next(m-y+1)+1;
Nex=B2[a[x][y]]._Find_next(y);
Nex=Nex-k+1;
B1[a[x][y]][m-y+1]=1;
B2[a[x][y]][y]=1;
if (Nex<=Pre) return;
Pre=max(max(Pre+1,1ll),y-k+1);
Nex=min(min(Nex,m+1),y+1);
if (Nex<=Pre) return;
delta[Pre]++;
delta[Nex]--;
}
void DEL(long long x,long long y)
{
long long Pre,Nex;
if (g[x][y]) return;
Pre=m-B1[a[x][y]]._Find_next(m-y+1)+1;
Nex=B2[a[x][y]]._Find_next(y);
Nex=Nex-k+1;
B1[a[x][y]][m-y+1]=0;
B2[a[x][y]][y]=0;
if (Nex<=Pre) return;
Pre=max(max(Pre+1,1ll),y-k+1);
Nex=min(min(Nex,m+1),y+1);
if (Nex<=Pre) return;
delta[Pre]--;
delta[Nex]++;
}
int main()
{
freopen("read.in","r",stdin);
// freopen("b.out","w",stdout);
scanf("%lld%lld%lld",&n,&m,&k);
bzz=1;
for (i=1;i<=n;i++)
for (j=1;j<=m;j++)
{
scanf("%d",&a[i][j]);
if (a[i][j]>2) bzz=0;
}
if (bzz==1)
{
does2();
return 0;
}
getg();
for (i=1;i<=k-1;i++)
for (j=1;j<=m;j++)
ADD(i,j);
for (i=k;i<=n;i++)
{
for (j=1;j<=m;j++)
ADD(i,j);
for (j=1;j<=m-k+1;j++)
f[j]=f[j-1]+delta[j],ans1=max(ans1,f[j]),ans2+=f[j];
for (j=1;j<=m;j++)
DEL(i-k+1,j);
}
printf("%lld %lld",ans1,ans2);
}
T3

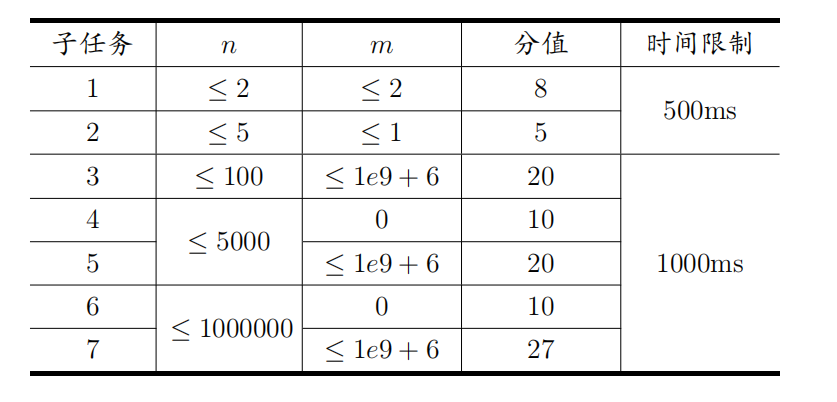
O((n^3))求逆矩阵的方法:把矩阵(A)与单位矩阵(I)放在一起,把(A)消成单位矩阵,I就会变成(A^{-1})
正解
找规律发现,答案等于
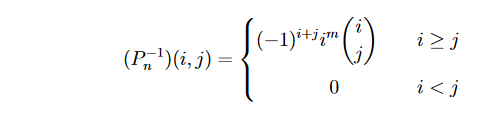
现在的难点在于求组合数的平方和(Sigma_{i=0}^{n}(C^{i}_{n})^2)
它等于

代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#define mod 1000000007
using namespace std;
long long n,m,i,j,k,L,pick,ans,T,xs,MI,S;
long long jc[3000005],invjc[3000005];
long long mi(long long x,long long y)
{
long long s=1;
while (y>0)
{
if (y%2==1) s=s*x%mod;
x=x*x%mod;
y/=2;
}
return s;
}
long long C(long long a,long long b)
{
return jc[a]*invjc[b]%mod*invjc[a-b]%mod;
}
int main()
{
freopen("read.in","r",stdin);
// freopen("c.out","w",stdout);
jc[0]=1;
for (i=1;i<=3000000;i++)
jc[i]=jc[i-1]*i%mod;
invjc[3000000]=mi(jc[3000000],mod-2);
for (i=3000000-1;i>=0;i--)
{
invjc[i]=invjc[i+1]*(i+1)%mod;
}
scanf("%lld%lld",&n,&m);
for (i=1;i<=n;i++)
{
MI=mi(i,m);
MI=MI*MI%mod;
S=MI*(C(2*i,i)-1)%mod;
ans=(ans+S%mod)%mod;
}
printf("%lld",ans);
return 0;
}