任务车间调度问题的混合整数规划模型

文献[1]的7.3节讲了一个任务车间调度问题。

一个车间生产套印纸张，分别套印蓝绿黄三种颜色。三种纸张根据需求分别在蓝、绿、黄三个机器上印刷，印刷时间如下表：

	印制颜色	纸1	纸2	纸3
机器1	蓝	45	20	12
机器2	绿		10	17
机器3	黄	10	34	28

纸张需要满足下图所示的印制次序：

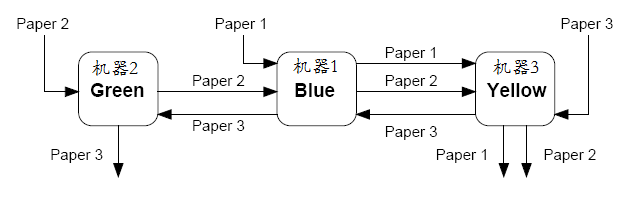
要求安排工艺调度（即安排纸张在各个机床上的加工时间）以使得总完成时间最短。

模型及求解

从上图可以读出纸张的印制次序为：

　　Paper 1: 1 --> 3

　　Paper 2: 2 --> 1 -->3

　　Paper 3: 3--> 1 --> 2

Paper 1 不需要在机器2上加工。为一致起见，设其在机器2上的加工时间为0，加工次序为3。得到下面的加工次序矩阵。

　　S={

　　　　1 3 2

　　　　2 1 3

　　　　3 1 2

　　}

设 T[i][j] 为纸张 j 在机器 i 上的加工时长。设 t[i][j] 为纸张 j 在机器 i 上的开始加工时刻。

模型的目标是极小化总完工时间tt:

　　min tt //(1)

显然tt必须大于等于三种纸张的各自完成时间：

　　tt >= t[S[j][3]][j]+T[S[j][3]][j] | j=1,...,3 //(2)

对任意纸张j和k，如果 j<>k，则他们在同一台机器上的加工时间不可冲突：

t[i][k] >= t[i][j] + T[i][j] 或 t[i][j] >= t[i][k] + T[i][k] | i=1,...,3;j=1,...,3;k=1,..,3;j<>k

上面是两个或约束，不可以直接写入混合线性规划的。解决办法是引入二值变量u[i][j][k]和大M，把上面的逻辑转换成两个联立约束：

　　t[i][k] >= t[i][j] + T[i][j] - M*u[i][j][k] | i=1,...,3;j=1,...,3;k=1,..,3;j<>k //(3)
　　t[i][j] >= t[i][k] + T[i][k] -M(1-u[i][j][k]) | i=1,...,3;j=1,...,3;k=1,..,3;j<>k //(4)

纸张需要满足加工次序约束：

　　t[S[j][k+1]][j] >= t[S[j][k]][j] + T[S[j][k]][j] |j=1,...,3; k=1,...,2 //(5)

完整的+Leapms模型：

min  tt               //(1)

subject to

    //tt大于等于三种纸张的各自完成时间：
　　tt >= t[S[j][3]][j]+T[S[j][3]][j] | j=1,...,3   //(2)

    //对任意纸张j和k，如果j<>k，则他们在同一台机器上的加工时间不能冲突：
    t[i][k] >= t[i][j] + T[i][j] - M*u[i][j][k] | i=1,...,3;j=1,...,3;k=1,..,3;j<>k   //(3)
　　t[i][j] >= t[i][k] + T[i][k] -M(1-u[i][j][k]) | i=1,...,3;j=1,...,3;k=1,..,3;j<>k //(4)

   //加工次序约束：
   t[S[j][k+1]][j] >= t[S[j][k]][j] + T[S[j][k]][j] |j=1,...,3; k=1,...,2  //(5)

where
   M is a number
   T[i][j] is a number | i=1,...,3;j=1,...,3
   S[i][j] is an integer | i=1,...,3;j=1,...,3
   tt is a variable of nonnegative number
   t[i][j] is a variable of nonnegative number | i=1,...,3;j=1,...,3
   u[i][j][k] is a variable of binary|i=1,...,3;j=1,...,3;k=1,..,3;j<>k

data

   T={
	45 20 12
	 0 10 17
	10 34 28
    }

    S={
　　　　1  3  2
　　　　2  1  3
　　　　3  1  2
　　}
    M=1000

求解过程

+Leapms>load
 Current directory is "ROOT".
 .........
        jobshop.leap
 .........
please input the filename:jobshop
================================================================
1:  min  tt               //(1)
2:
3:  subject to
4:
5:      //tt大于等于三种纸张的各自完成时间：
6:  　　tt >= t[S[j][3]][j]+T[S[j][3]][j] | j=1,...,3   //(2)
7:
8:      //对任意纸张j和k，如果j<>k，则他们在同一台机器上的加工时间不能冲突：
9:      t[i][k] >= t[i][j] + T[i][j] - M*u[i][j][k] | i=1,...,3;j=1,...,3;k=1,..
,3;j<>k   //(3)
10:  　　t[i][j] >= t[i][k] + T[i][k] -M(1-u[i][j][k]) | i=1,...,3;j=1,...,3;k=1
,..,3;j<>k //(4)
11:
12:     //加工次序约束：
13:     t[S[j][k+1]][j] >= t[S[j][k]][j] + T[S[j][k]][j] |j=1,...,3; k=1,...,2
//(5)
14:
15:  where
16:     M is a number
17:     T[i][j] is a number | i=1,...,3;j=1,...,3
18:     S[i][j] is an integer | i=1,...,3;j=1,...,3
19:     tt is a variable of nonnegative number
20:     t[i][j] is a variable of nonnegative number | i=1,...,3;j=1,...,3
21:     u[i][j][k] is a variable of binary|i=1,...,3;j=1,...,3;k=1,..,3;j<>k
22:
23:  data
24:
25:     T={
26:     45 20 12
27:      0 10 17
28:     10 34 28
29:      }
30:
31:      S={
32:  　　　　1  3  2
33:  　　　　2  1  3
34:  　　　　3  1  2
35:  　　}
36:      M=1000
================================================================
>>end of the file.
Parsing model:
1D
2R
3V
4O
5C
6S
7End.
..................................
number of variables=28
number of constraints=45
..................................
+Leapms>mip
relexed_solution=64; number_of_nodes_branched=0; memindex=(2,2)
The Problem is solved to optimal as an MIP.
找到整数规划的最优解.非零变量值和最优目标值如下：
  .........
    t1_1* =42
    t1_2* =10
    t1_3* =30
    t2_1* =97
    t2_3* =42
    t3_1* =87
    t3_2* =30
    t3_3* =2
    tt* =97
    u1_1_2* =1
    u1_1_3* =1
    u1_3_2* =1
    u2_1_2* =1
    u2_1_3* =1
    u2_3_2* =1
    u3_1_2* =1
    u3_1_3* =1
    u3_2_3* =1
  .........
    Objective*=97
  .........
+Leapms>

求解过程（按+查看）

求解结果

+Leapms>mip
relexed_solution=64; number_of_nodes_branched=0; memindex=(2,2)
The Problem is solved to optimal as an MIP.
找到整数规划的最优解.非零变量值和最优目标值如下：
  .........
    t1_1* =42
    t1_2* =10
    t1_3* =30
    t2_1* =97
    t2_3* =42
    t3_1* =87
    t3_2* =30
    t3_3* =2
    tt* =97
    u1_1_2* =1
    u1_1_3* =1
    u1_3_2* =1
    u2_1_2* =1
    u2_1_3* =1
    u2_3_2* =1
    u3_1_2* =1
    u3_1_3* =1
    u3_2_3* =1
  .........
    Objective*=97
  .........
+Leapms>

反向生成Latex数学概念模型

+Leapms提供从+Leapms模型向Latex数学概念模型的转换。

当模型调整和测试完毕，使用+Leapms的latex命令可生成本问题的如下数学概念模型：

参考文献

[1] Christelle Guéret, Christian Prins, Marc Sevaux. Applications of optimization with Xpress-MP (Translated and revised by Susanne Heipcke). Dash Optimization Ltd. 2000