第一篇黑题题解qwq
由于窝在做zhx的模拟题被2-SAT加线段树优化建边搞炸了,所以一气之下来学了这两个东西ww
这篇就是线段树优化建边
直接步入正题,先来看题目
题目描述
在一条直线上有(N)个炸弹,每个炸弹的坐标是 (X_i),爆炸半径是 (R_i),当一个炸弹爆炸时,如果另一个炸弹所在位置(X_j) 满足: (X_i-R_ileq X_j leq X_i+R_i) ,那么,该炸弹也会被引爆。 现在,请你帮忙计算一下,先把第(i)个炸弹引爆,将引爆多少个炸弹呢?
答案对(1000000007)取模
输入格式
第一行,一个数字(N),表示炸弹个数。 第(2)~(N+1)行,每行(2)个数字,表示(X_i ,R_i),保证(X_i)严格递增
说明/提示
(N leq 500000 , -10^{18} leq X_i leq 10^{18},0 leq R_i leq 2 imes 10^{18})
题解
这道题要求的其实就是引爆每一个炸弹所附加的引爆炸弹的数量
先想最暴力的方法,显然就是对每一个点进行搜索,算出他所能到达的点的数量
那么就可以对能够互相到达的两个点连边,统计答案的时候直接进行DFS。
时间复杂度(O(n^2)),空间复杂度也是(O(n^2)),显然过不了
我们尝试找一下这个题目特殊的性质:每一个点所能覆盖到的点在一个区间里,也就是说这个点所能连到的点都要在这个区间里。换句话说,对于这个区间里的每一个点都要连一条边。而存贮这些边是导致空间爆炸的原因,遍历这些边则是导致时间爆炸的原因。那么要优化复杂度,显然要优化存储边的方式。
接下来考虑怎么优化?
先来看几张图

我们现在要把点0向1~5这些点连边,一共连了五条边
但是如果我们把这些点放到线段树上
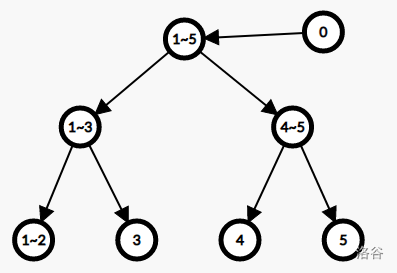
发现只需要把0点向区间1~5连一条边就行了
这样就大大减少了连边的数量
可以证明,给n个点连边,通过线段树优化的方式,复杂度由(O(n^2))优化到了(O(nlogn))(证明略)
连完边之后,可以发现能够相互到达的点一定在同一个强连通分量里面,于是直接跑tarjan缩点,记录每一个强联通分量里面的节点数量,代表这个强连通分量里面的点能够到达的点的个数。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read()
{
ll ans=0;char last=' ',c=getchar();
while(c<'0'||c>'9') last=c,c=getchar();
while(c>='0'&&c<='9') ans=(ans<<3)+(ans<<1)+c-'0',c=getchar();
if(last=='-') ans=-ans;
return ans;
}
const ll N=500050,mod=1e9+7;
ll head[N<<4],Head[N<<4],ecnt,Ecnt;
struct edge{ll to,nxt;}edg[N<<5],Edg[N<<5];
inline void add_edge(int u,int v)
{
edg[++ecnt].to=v;
edg[ecnt].nxt=head[u];
head[u]=ecnt;
}
inline void Add_edge(int u,int v)
{
Edg[++Ecnt].to=v;
Edg[Ecnt].nxt=Head[u];
Head[u]=Ecnt;
}
ll n,node;
ll X[N],R[N];
ll id[N<<4],w[N<<4];
void build(int cnt,int l,int r)
{
if(l==r)
{
id[l]=cnt;node=max(node,ll(cnt));w[cnt]=1;
return;
}
ll mid=l+r>>1;
build(cnt<<1,l,mid);build(cnt<<1|1,mid+1,r);
add_edge(cnt,cnt<<1),add_edge(cnt,cnt<<1|1);
}
void add(int cnt,int l,int r,int nl,int nr,int x)
{
if(nl<=l&&nr>=r)
{
add_edge(x,cnt);
return;
}
ll mid=l+r>>1;
if(nl<=mid) add(cnt<<1,l,mid,nl,nr,x);
if(nr>mid) add(cnt<<1|1,mid+1,r,nl,nr,x);
}
ll dfn[N<<4],low[N<<4],ind,scc[N<<4],cnt,in[N<<4],s[N<<4],top,W[N<<4];
void tarjan(int x)
{
low[x]=dfn[x]=++ind;
s[top++]=x;
in[x]=1;
for(int i=head[x];i;i=edg[i].nxt)
{
int v=edg[i].to;
if(!dfn[v])
{
tarjan(v);
low[x]=min(low[x],low[v]);
}
else if(in[v]) low[x]=min(low[x],dfn[v]);
}
if(dfn[x]==low[x])
{
cnt++;
while(s[top]!=x)
{
top--;
in[s[top]]=0;
scc[s[top]]=cnt;
W[cnt]+=w[s[top]];
}
}
}
void rebuild()
{
for(int u=1;u<=node;u++)
{
for(int i=head[u];i;i=edg[i].nxt)
{
int v=edg[i].to;
if(scc[u]==scc[v]) continue;
Add_edge(scc[u],scc[v]);
}
}
}
queue<int> Q;
ll f[N<<4],vis[N<<4];
void dfs(int u)
{
if(f[u]) return;
vector<int> a;
f[u]=W[u];
for(int i=Head[u];i;i=Edg[i].nxt)
{
int v=Edg[i].to;
dfs(v);a.push_back(v);
}
for(int i=0;i<a.size();i++)
{
if(vis[a[i]]==u)continue;
vis[a[i]]=u;f[u]+=f[a[i]];
}
}
ll ans=0;
int main()
{
n=read();
for(int i=1;i<=n;i++) X[i]=read(),R[i]=read();
build(1,1,n);
for(int i=1;i<=n;i++)
{
ll l,r;
l=lower_bound(X+1,X+1+n,X[i]-R[i])-X;
r=upper_bound(X+1,X+1+n,X[i]+R[i])-X-1;
add(1,1,n,l,r,id[i]);
}
for(int i=1;i<=node;i++) if(!dfn[i]) tarjan(i);
rebuild();
for(int i=1;i<=cnt;i++) dfs(i);
for(int i=1;i<=n;i++) ans=(ans+i*f[scc[id[i]]])%mod;
cout<<ans;
}