概率
某个事件A发生的可能性的大小,称之为事件A的概率,记作P(A)。
假设某事的所有可能结果有n种,每种结果都是等概率,事件A涵盖其中的m种,那么P(A)=m/n。
例如投掷一枚骰子,点数小于3的概率为2/6=1/3。
如果两个事件A和B所涵盖的结果没有交集,那么P(A或B发生)=P(A)+P(B)
还是掷骰子
P(点数小于3或点数大于4)=2/6+2/6=2/3
如果A和B所涵盖的结果有交集
那么P(A或B发生)=P(A)+P(B)-P(A与B同时发生)
P(点数小于3或点数为偶数)=2/6+3/6-1/6=2/3
记事件B为“事件A不发生”
那么P(A)+P(B)=1,即P(B)=1-P(A)
P(点数不小于3)=1-2/6=2/3
在两个互不干扰的事中,事件A在其中一件事中,事件B在另外一件事中
那么P(A与B同时发生)=P(A)*P(B)
掷两个骰子,P(第一个点数小于3且第二个点数为偶数)=(2/6)*(3/6)=1/6
期望
事件A有多种结果,记其结果的大小为x,那么x的期望值表示事件A的结果的平均大小,记作E(x)。
E(x)=每种结果的大小与其概率的乘积的和。
例如,记掷一枚骰子的点数为x
E(x)=1*(1/6)+2*(1/6)+3*(1/6)+4*(1/6)+5*(1/6)+6*(1/6)=7/2
若c为常数,那么:
E(x+c)=E(x)+c,E(c*x)=c*E(x)
期望
记两个事件的结果分别为x,y
E(x+y)=E(x)+E(y)
例如:E(语文成绩+数学成绩)=E(语文成绩)+E(数学成绩)
任何情况下都成立
若两个事件互相独立,E(x*y)=E(x)*E(y)
E(语文成绩*数学成绩)=E(语文成绩)*E(数学成绩)
概率和期望的计算
概率与期望的计算有一个共同的计算技巧:
若事件所产生的所有方案都是等概率的,那么一些概率与期望即可转化为一个计数问题,算出后再除以总方案数即可。
如求事件符合条件A的概率,则转化为对符合A的方案数的计数问题;若求方案的某种价值的期望值,则转化为所有方案的价值总和的计数问题。
概率与期望的计算也经常用的其加法和乘法规则。
尤其是期望的加法规则,在期望的计算中十分常用。如求最大值与最小值之差的期望,则分别求二者的期望值再作差即可。
应用乘法规则时,要注意事件是否互相独立。
概率与期望还可以通过列方程的方法计算。
有4张卡片,写着0,1,2,3,每次抽出一张并放回,反复抽,抽出0为止。问抽取的次数的期望值。
设抽取次数为x,则:
x=1+x*3/4
x=4
不放回的话就枚举,反正情况也不多
概率DP期望DP

比较简单的概率dp
设f[i][j]为小球经过第i行第j列的概率。
f[1][1]=1 (即起始状态概率为1 )
f[i][j]=f[i-1][j-1] * [(i-1,j-1)有钉子]*1/2
+f[i-1][j] * [(i-1,j)有钉子]*1/2
+f[i-2][j-1] * [(i-2,j-1)没有钉子]
至于分数输出,自定义分数数据类型并用gcd化简分数即可。
Bzoj5004 开锁魔法II
有 n 个箱子,每个箱子里有且仅有一把钥匙,每个箱子有且仅有一把钥匙可以将其打开。现在随机打开 m 个箱子,求能够将所有箱子打开的概率。
100组数据,k<=n<=300。
给你一个排列
会形成一些环
求一共选择m个,在每一个环上都至少选择一个的方案数
预处理出每个环的点数 c[i] 以及其后缀和 sum[i] 。
设 f[i][j] 表示前 i 个环中选出 j 个点,满足最终条件每个环都选的方案数。初始化 f[0][0]=1 。
枚举 i 和 前 i 个环选的点数 j 、第 i 个环选的点数 k。
可得
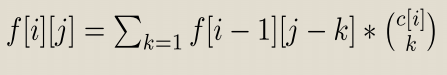
BZOJ5091 摘苹果
在花园中有n棵苹果树以及m条双向道路,每条道路的两端连接着两棵不同的苹果树。假设第i棵苹果树连接着di条道路。小Q将会按照以下方式去采摘苹果:
1.随机移动到一棵苹果树下,移动到第i棵苹果树下的概率为di /2m,但不在此采摘。
2.重复以下操作k次:等概率随机选择一条与当前苹果树相连的一条道路,移动到另一棵苹果树下,假设当前位于第i棵苹果树下,则他会采摘ai个苹果,多次经过同一棵苹果树下会重复采摘。
请计算小Q期望摘到多少苹果。n,k<=100000,m<=200000
E(x1+x2+...+xn)=ΣE(xi)(i=1~n)
xi=0--->0*P
xi=1--->f[k][i]*a[i]
f[k][i]为第k轮到i的概率
xi表示是否在第i棵苹果树下
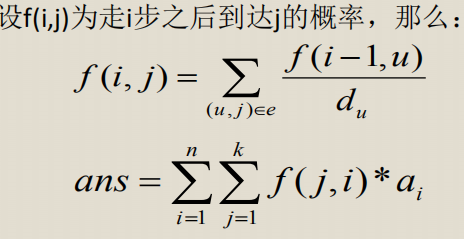
发现到达每一个点的概率都是di/2m
为什么?
首先到达的树的概率为di/2m
然后这个点经过每一条边到达别的点的概率是di/2m*1/di=1/2m
这样每个点的概率就是他的边连的点到他的总概率就是di/2m
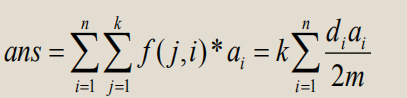
BZOJ4832 抵制克苏恩
你有一个英雄和若干奴隶主,对方每次攻击会从你的英雄和奴隶主中随机选一个造成一点伤害。奴隶主受到攻击后,体力为0则死亡,否则若场上奴隶主少于7个,则召唤一个3点血量的奴隶主。
有T局游戏,每局给出初始奴隶主的数量(<=7)和血量(<=3),给出k,求对方攻击k次后你的英雄受到的总伤害值的期望。
T<=100,k<=50。
f[i][a][b][c]还剩下i轮,血量=1,2,3的奴隶数量为a,b,c
如果打到英雄1/S
f[i][a][b][c]+1=f[i-1][a][b][c]
打到a中的奴隶a/S
f[i][a][b][c]=f[i-1][a-1][b][c]
打到b中的奴隶b/S
f[i][a][b][c]=f[i-1][a+1][b-1][c]
打到c中的奴隶c/S
f[i][a][b][c]=f[i-1][a][b+1][c-1]
对于增加奴隶单独判断
出的概率是1,但是接受的概率不一定是1 ????
取答案时也有问题,因为不知道状态
我们考虑逆序?
就可以了
NOIP2016 换教室
小A的学校可以视为一个v个点的无向图,他有n门课程要按顺序上课,其中第i门课程要在节点ai进行,但还有一个备选地点bi。现在小A有m个申请机会,若申请第i门课,那么将有ki的概率使课程搬到bi进行。每门课最多申请一次,而且要在全部申请完成后才知道是否成功,m次机会不必全部用完。他如何申请才能最小化在上课地点间移动的距离的期望值。求该期望值。
◦ v<=300,n,m<=2000
先floyd一遍
dp[i][j]表示前i个课程申请j次的期望距离
看能不能转移
不申请
dp[i][j]-->dp[i+1][j]
好像并不能
加一维
dp[i][j][0/1]表示前i个课程申请j次,i有没有申请的期望距离
f[i][j][0]=Min{ f[i-1][j][0]+dis(a[i-1],a[i]) ,
f[i-1][j][1]+k[i-1]*dis(b[i-1],a[i])+(1-k[i-1])*dis(a[i-1],a[i])}
f[i][j][1]也是同理,只需要考虑i和i-1都是否申请上即可。
时间复杂度O(v^3+nm)
BZOJ1076 奖励关
有n轮游戏和m种宝物,每种宝物有分数Pi(可以为负),每轮游戏会等概率抛出一种宝物,你可以选择吃或不吃。第i种宝物还有一个限制集合Si,表示只有在Si中的宝物都吃过后,才能吃第i种宝物。
求最优策略下的期望得分。
n<=100,m<=15
到了一个物品,如果你知道吃和不吃之后所能产生的期望值的话,就直接取max就好了
f[i][s]表示还剩i轮,吃的集合是s的最大期望值
f[i][S]= ( ∑Max{ f[i-1][S] , f[i-1][S∪k]+a[k] } )/m
初始f[0][S]=0。ans=f[n][0]
最套路的斜率优化
hdu3507
要输出N个数字a[N],输出的时候可以连续的输出,每连续输出一串,它的费用是 :这串数字和的平方加上一个常数M。
0 ≤ n ≤ 500000, 0 ≤ M ≤ 1000
n^2
dp[i]表示前i的最小费用
转移的时候就枚举断点
斜率优化:
dp[i]=min{dp[j]+ (sum[i]-sum[j])^2 +M}
考虑k和j那个更优
设k<j,j优于k
dp[j] + (s[i]-s[j])^2 + M<dp[k] + (s[i]-s[k])^2 + M
dp[j] + s[j]^2 - 2s[i]s[j]<dp[k] + s[k]^2 -2s[i]s[k]
(dp[j] + s[j]^2 - dp[k] + s[k]^2)<2s[i](s[j] - s[k])
除过去
((dp[j] + s[j]^2 - dp[k] + s[k]^2)) / (s[j] - s[k]) < 2s[i]
把(s[j],dp[j]+s[j]^2)看做点
点j和点k的斜率
找平面上的1,2,...,i-1的决策点
如果<的话说明后者(j)比前者(k)优
考虑三个决策点的关系
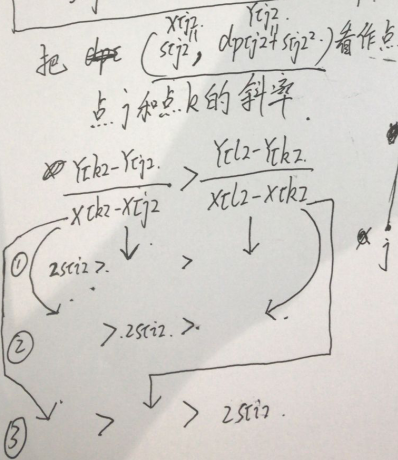
发现不管s[i]是多少,k都没有什么卵用
配合图理解一下
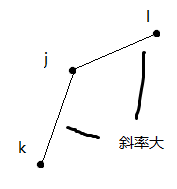
也就是说如果前面的斜率大于后面的话就没什么卵用了
那么我们可以维护一个下凸壳(特点:斜率单增)
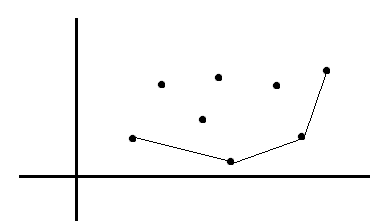
如何在这上面找决策点?
在这一个决策点之前,优于斜率的关系,后者肯定比前者优
而在这个决策点之后,前者比后者优
直接二分就可以了,查找斜率比2s[i+1]小的编号最大的点
怎么维护
我们发现i递增是,s[i]是单调递增的,决策点也在递增
那么我们就可以搞一个单调队列
每次增加一个点就判断一下,如果不行就出队
对于队首,由于决策点递增,所以如果当前的队首不是决策点,那么在之后他也不可能是,这时就直接让他出队
这样每次的决策点就是队首的点
- 推式子
- 拆平方
- 约掉
- 把和i有关的放在右边,把j和k放在左边
- 把j放在一起,k放在一起
bzoj3156


◦f[i]=min(f[j]+(i-j-1)*(i-j)/2+a[i])。
◦设k>j,且k优于j。
◦f[k]+(i-k)*(i-k-1)/2+a[i]<f[j]+(i-j)*(i-j-1)/2+a[i]
◦设K=k+1,J=j+1 为了好推
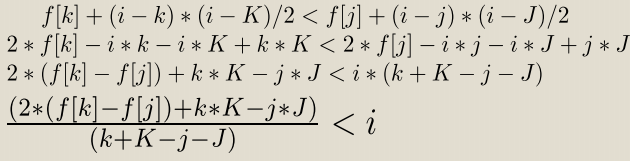
bzoj4321
编号为1~n的人排成一排,问有多少种排法使得任意相邻两人的编号之差不为1或-1。
n<=1000
f[i][j]表示前i个有j个相邻对的方案数
考虑i插在哪里
不破坏空位且不与 i 相邻、不破坏空位且与 i 相邻、破坏空位且不与 i 相邻、破
坏空位且与 i 相邻(只发生在 g 的转移)4种。
发现如果插在i和i-1中间是既+1又-1,这样就没法转移了
f[i][j][0/1]表示前i个有j个相邻对,i和i-1是否相邻的方案数
BZOJ2560 串珠子
有n个珠子,第i和j个珠子之间有c[i][j]条不同的绳子可选。每对珠子之间可以选择不连绳子,也可以选择用其中一种绳子连接。
问有多少种方案能使n个珠子成为连通图。
n<=16
总方案数∏(c[i][j]+1)
容斥一下
如果不连通,一号点在某一个连通块内,枚举一号点联通的集合,然后总方案数-不连通的方案数
按照一号点联通的集合T分类,dp[t]表示t集合不连通的方案数
集合外面随便连
f[s]表示合法情况
g[s]表示所有情况
就是枚举合法情况1号点所在的联通块的点集i,那么这里不合法的情况就是g[s^t]*f[t],我们减去这些情况,就能求出f[s]了。
f[s]=g[s]-Σf[t]g[s^t] (T∈S && T!=S && T的最低位∈S)
复杂度3^n