内容提要
动态规划
状压DP
其他DP
状压dp
给你一堆平面坐标系上的点,有一个人刚开始在一号点,想让他走完其他的点,问你最短的距离是多少

TSP问题(旅行商问题)
一个非常经典的NP-hard问题(就是你写的最快也是指数的级别,不可能比2^快)
从一号点出发把其他的都走一遍,显然每一个点只需要去一次,并且两点之间线段最短
显然贪心不对(复杂度就对不起来好吗)
因为我们学的dp,所以我们要运用dp的方法解(滑稽
枚举可行的方案
比如有6个点,已经走了1,2,5
然后枚举状态

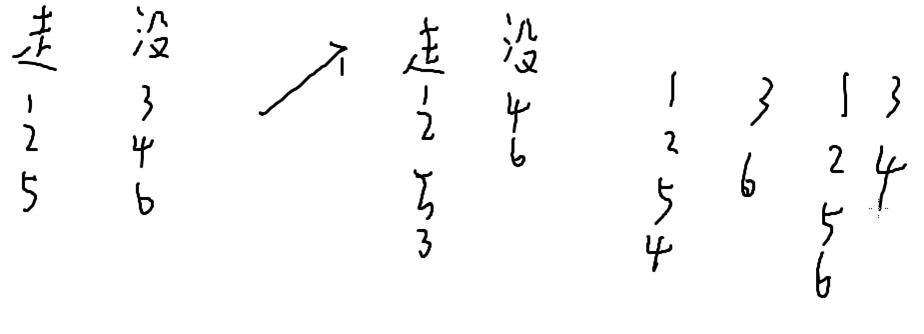
我们希望把集合表示成数组的下标,怎么做???
用二进制
我们可以构造一个n位的二进制数

对每个元素有两种状态,就是它在这个集合里面或者不在
对于二进制有两种状态,就是1或0
这两个可以想到一起
如果这个元素在这个集合里面,二进制数的第i位就是1
否则是0
这个二进制数和这个点集是等价的,而这个二进制数有自己唯一对应的一个十进制数
f[s][i]一个n位的二进制数
从起始点走到i点,且经过的点的集合是s的最短距离
s:已经走过的点所对应的集合
i:现在停留在i点
比如集合为{1,2,4,6}最后到达的是点6,那么s就对应这个集合,i就是6
显然初始化就是f[1][1]=0
转移方程呢?
我们考虑怎么走,这样的话就要枚举点
j:1--n
状态转移方程:
因为每个点只走一次
如果j∉s
f[s∪{j}][j]=f[s][i]+dis[i][j]
伪代码以及非常详细的注释解释
int n,f[233]; double f[2^n][n]; //因为点集是用二进制数表示的,如果都在的话最多就是2^n //每一个点在或者不在,所以是n double dis(int i,int j) { return sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]));//距离公式 } int main() { cin>>n; for(int a=0;a<n;a++) { cin>>x[a]>>y[a]; //注意这里是从0开始,因为二进制最低位是从2^0开始的 } for(int a=0;a<(1<<n);a++) { for(int b=0;b<n;b++) { f[a][b]=1e+20;//因为要最小值,所以赋值为无穷大 } } f[1][0]=0//因为下标都减了一 ,所以从零号点开始 //二进制数为 0 0 0 0....0 0 1转化到十进制就是1 //应该先枚举s还是i? //我们走的时候到达的点不断变多,也就是二进制的0不断变成1 //也就是s不断变大,所以把s从小到大来枚举 for(int s=1;i<(1<<n);s++)//枚举已经走过的点 { for(int i=0;i<n;i++)//枚举停留的点 { //但是如果这样的话有可能i不在集合s中,所以我们要判断 if(((s>>i)&1)==1)//右移i位的话他的第i位就移到了最低位 //如果第i位=1的话,就说明i在这个集合里面 { //转移:从剩下没有走过的点里枚举 for(int j=0;j<n;j++) { if(((s>>j)&1)==0)//如果不在这个集合中,就说明可以走 { f[s|(1<<j)][j]=min(f[s|(1<<j)][j],f[s][i]+dis(i,j));//s|(1<<j):把s的二进制第j位变成1 } } } } } double ans=1e+20; for(int a=1;a<n;a++) ans=min(ans,f[(1<<j)-1][a]);//枚举终点 cout<<ans<<endl; }
它的时间复杂度是O(n^2 * s^n)
空间复杂度O(2^n * n)
(一秒钟的运算量在3*10^8~10^9之间)
差不多n<=20
补充一些复杂度有关的知识
n<=12(O(n!)的复杂度,直接暴搜)
n<=22 (状压)
n<=32 (直接放弃)
n<=50 (直接放弃)
n<=100 (O(n^3))
n<=1000 (O(n^2))
n<=10^5 (数据结构)
n<=10^6 (线性算法)
其他DP
题目每多一个条件,就多一个维度
N*M的方格图
只能向右或者向下
走到右下的方案数?
走到右下的最小代价?
用f[i][j]表示走到第n行第m列的方案数
f[1][j]=f[i][1]=1
转移:f[i][j]=f[i-1][j]+f[i][j-1]
数字三角形
f[i][j]表示走到第i行第j列的最大值是多少
边界条件:f[1][1]=a[1][1]
走要一个点,要么从左上走到,要么走上面走到
转移:f[i][j]=max(f[i-1][j-1]+f[i-1][j])+a[i][j]
改造一波:
让这条路径权值之和%m最大
n,m<=100
直接用数字三角形的dp方程加上模是不行的,因为不再满足最优子结构原则了。
我们考虑加维度
状态:bool数组f[i][j][k]代表走到第i行第j列是路径权值和%m=k可不可能
转移方程:f[i][j][k]=f[i-1][j-1][(k-a[i][j])%m]||f[i-1][j][(k-a[i][j])%m]
边界f[1][1][a[1][1]%m]=true
然后找到一个最大的k
最长上升子序列
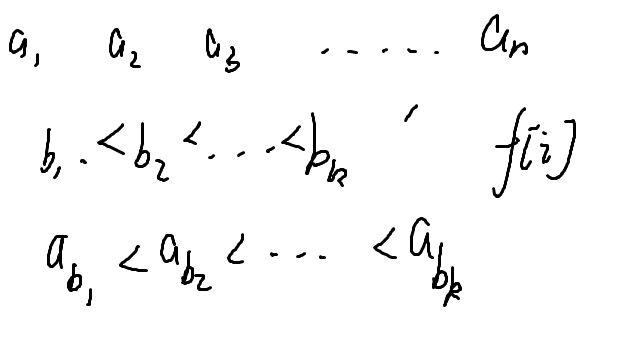
n<=1000
考虑f[i]以i号点结尾的最长上升子序列的长度
f[i]=max(f[j]+i)
复杂度O(n^2)
当n加强到10^5时
换一个数据结构
线段树
v=max(a1,a2,...,an)
建一棵大小为n的线段树
按值进行左右划分
每一次算f[i]时,边计算边将a[i]修改为f[i]
用到区间max值和单点修改
背包:背包九讲
最基本的背包问题:0/1背包(每个物品放或者不放)
你现在有n个物品,第i个物品的价值为wi体积为vi,你有一个大小为m的背包,求在保证放进背包的物品的体积之和在不超过背包容积的情况下使得价值最大
状态f[i][j]:前i个物品用了j的体积最大价值是多少
转移:第i个物品放进背包或者不放进背包
不放:f[i][j]=f[i+1][j]
放:f[i][j]+w[i]=f[i+1][j+v[i+1]]
复杂度O(n,m)
无穷背包问题:每个物品都有无数个
比较直观的想法:枚举每个物品到底用多少个
f[i][j]+x*w[i+1]-->f[i+1][j+x*v[i+1]]
但是这样就会爆复杂度O(n*m^2)
转移方程:f[i][j]=max(f[i-1][j],f[i][j-v[i]]+w[i]
f[i][j]<--f[i][j-v[i]]<--f[i][j-2v[i]]
复杂度O(nm)
有限背包:告诉你每个物品多少个
枚举用的物品数
求在[l,r]中满足各位数字之积为k的数有多少个
f[i][j][k]:填到第i位,j=0:< j=1:= k:记录目前的乘积
枚举下一位数
k最大到9^18,显然不行
因为填的数在1~10以内
k:2^a * 3^b * 5^c * 7^d
改写状态:
f[i][j][a][b][c][d]:填到第i位,j=0:< j=1:= 2^a· * 3^b * 5^c * 7^d
