1.算数基本定理:
对于任意的大于1的正整数N,N一定能够分解成有限个质数的乘积,即
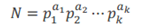
其中P1<P2<...<Pk,a1,a2,...,ak>=1;
证:
存在性:
若存在最小的N不满足条件,当N为质数是,显然不成立;当N为合数时,存在P,使得N=P*(N/P),N/P<N,与假设N为最小的矛盾,故一定存在;
即:假设N为最小的
当N为质数直接gg
当N为合数还是gg
故不存在...
唯一性:
假设N的分解不唯一
设存在最小的N,使得N=p1r1 p2r2 .... pkrk且N=q1t1 q2t2 .....qntn
则p1|q1t1 q2t2 .....qntn
假设p1=q1,且r1>=t1,那么两个式子同时除以p1t1,
有p1r1-t1.....=q10 .....
而经过变换后的式子要小于原式
这与假设N为最小的不满足的矛盾
(A是一个<=n的正整数 两个条件至少有一个成立)
2.素数的判定
Miller-rabin素性测试
如果n为素数,取a<n,设n-1=d*2r,则要么ad≡1(mod n)要么存在0<=i<r,使得ad*2^t≡-1(mod n),要么存在0<=i<r,使得ad*2^t≡-1(mod n)(有可能都满足)
任意一个a,如果满足这两个条件,n有可能是质数
但a如果不满足这两个条件中的任何一个,它一定不是质数
找k个a,如果都满足这两个条件,k-1个“更”有可能是质数
如果n是素数,取a<n,舍n-1=d*2r,则要么ad≡1(mod n),要么存在0<=i<r,使得a
选2,3,5,7,13,29,37,89,int范围内不可能出错
部分代码:
1 int gg[8]={2,3,5,7,13,29,37,89}; 2 3 long long kuaisumi(long long a,long long b1,long long c) 4 { 5 long long i=a; 6 while(b1) 7 { 8 if(b1&1) 9 { 10 s=(s*i)%c; 11 } 12 i=(i*i)%c; 13 b1>>=1; 14 } 15 return s%c; 16 } 17 18 bool miller_rabin(int a,int n) 19 { 20 int d=n-1,r=0; 21 while(d%2==0) 22 d/=2,r++; 23 int x=kuaisumi(a,d,n); 24 if(x==1)return true; 25 for(int i=0;i<r;i++) 26 { 27 if(x==n-1)return true ; 28 x=(long long )x*x%n; 29 } 30 return false;//可以对照素性测试看 31 } 32 33 bool is_prime (int n) 34 { 35 if(n<=1)return false ; 36 for(int a=0;a<8;a++) 37 if(n==gg[a])return true;//一个个试 38 for(int a=0;a<8;a++) 39 if(!miller_rabin(gg[a],n))return false; 40 return true; 41 }
3,最大公因数
Gcd(a,b)=max{x(x|a,x|b)}
欧几里得算法的核心思想
gcd(a,b)=gcd(b,a-b)==>gcd(a,b)=gcd(b,a%b)
4.裴蜀定理
给定a,b,c,则ax+by=c有整数解的充要条件是gcd(a,b)|c
来证一下
不妨使用唯一分解定理
充分性:
d=gcd(a,b),
则d|a,d|b==>d|ax+by=c==>d|c充分性证毕
必要性:
设d=gcd(a,b),s=min(ax+by),s>0
a/s=q......r(0<=r<s)==>r=a-qs=a-q(ax+by)=(1-qx)a-qyb
因为s=min(ax+by),所以r=0==>s|a&&s|b==>
1-------s|gcd(a,b)
s=ax+by=b(nd)+y(md)==>
2-------d|s
综合1,2,得到s=d
证毕
一个应用
请证明:设p为质数,若p|ab,则p|a或p|b
证:
当p|a时,显然成立
否则,gcd(p,a)=1==>xp+ya=1
b=b*1=b(xp+ya)=pxb+yab
p|pxb==>p|yab
5.拓展欧几里得
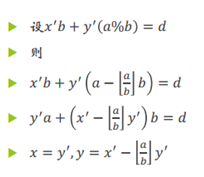

6.中国剩余定理



x≡a1(mod p1) x≡a2(mod p2) O(min(p1,p2))
x=a1,a1+p1,a1+2p2....,x<=a1+p2p1
过不了的情况:k=2,两个数都在1e9左右