什么是图鸭?
什么是有向图鸭?

什么是权鸭?
就是点和边的价值辣
什么还有负权??!
什么是环啊?
就是从一个点出发能走回自己辣
注意重边!!!
有向无环图:缩写:DAG
顾名思义,就是一个没有环的有向图
简单路径:没有经过重复点的路径
什么是树鸭?
包含n个点,n-1条边的连通图
树没有环。一般来说是个无向图,但是我们通常会顶根
完全图
图上有n个点,有n2条边
竞赛图
有方向的完全图,但边数还是n2,不是2n2
基环树:环上挂着棵树的东西
仙人掌:每一条边最多属于一个环的东西

图的存储方式:
1.邻接矩阵
如果(u,v)之间有连边,那么邻接矩阵a[u][v]的值就是边权

用处:跑弗洛伊德
更为常见的方式


如果毒瘤出题人让你做很长很长的dfs还不给你开栈,那就只能手写了
遍历方法

三种dfs序:

是树的遍历顺序
前序遍历:头 左 右(也就是最常用的遍历顺序)
中序遍历:左 头 右
后序遍历:左 右 头
给出前序,中序,写后序:
前序第一个:树根
在中序中找根,根左边是左子树,右边是右子树,把它们从原序列里拎出来,看前序序列中的根,递归搞
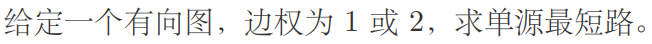
只用dfs,bfs怎么过?
维护三个集合,一个记录距离为d的,一个记录距离为d+1的,一个记录距离为d+2的
先枚举距离为d的集合的点,看他的出边是1还是2,然后把终点扔到对应的集合里依次更新每个集合

边长均为1
这里用dij求出每个点到起点的最短路d[u],然后求出最短路图
求最短路图:如果d[u]+1==d[v],则留下这条边
看在最短路图上的v,如果v入度为1,则一定会改变,若不为1,则不会改变
拓扑排序:

如果有环,则拓扑序不存在

最后每个点被拿出的顺序就是拓扑序

vi向i连边
跑拓扑序即可

把每一个任务拆成两个点(起始,结束)
操作1就是要求v的起始时间在u的结束时间之后
对于操作2:v的结束时间在u的开始时间之后,u的结束时间在v的开始时间之后
按照这个关系连边(注意起始时间要向结束时间连边)

还是不准用dij,spfa
拓扑+dp

判冲突:拓扑排序判环:
判顺序不能确定:看队列里面是否永远只有<=1个元素
因为如果某一时刻有两个元素,那么接下来取哪个元素都可以,就会造成多个合法的拓扑排序,也就是没有唯一的顺序。

标记的那一行告诉我们有向边不会在环里面
环里面的边都是无向边,无向边都是正权的
所以对于环,用dij进行类似缩点般的操作,然后对有向边用拓扑排序求最短路
更秀的操作:
对于无向边,跑dij,对于有向边,像拓扑一样跑dij
emm说人话:
这张图上只有由无向边构成的联通块,每个联通块之间由有向边连接。
我们可以把每个连通块视作一个大点,这样就是一个DAG.找到入度为0的大点,先跑dij
然后通过有向边,类似跑拓扑排序一样,更新新的大点。在大点里的点就跑dij来更新每个真实的小点的dis值
最短路

为什么空间复杂度是O(n2)
因为第一维k没有用,所以只需要二维f[i][j]记录i到j的当前的最短路即可
记住k在第一维枚举
Floyed传递闭包:
询问u能否到达v(u,v为图中任意一点)

若i到k可达,k到j可达,则i到j可达
毒瘤一点

弗洛伊德快速幂??
弗洛伊德有结合律
Dijkstra

就是将已经求出到起点的最短路的点放进一个集合,枚举集合里的点的出边,更新与其相邻的点的dis值
堆优化的dij

Bellman ford
每一次都拿m条边更新,直至dis数组确定下来
没有负环:n个点m-1条最短O(nm)

拿队列进行优化:spfa
只有当d[v]变小之后,才拿v进行更新其他点
用队列维护d值改变的点,依次取队首,进行更新
可能会被毒瘤数据卡成O(nm)
手写队列的常数就小了辣