T3:



... ...不会
选k个集合,每个集合的价值就是线段交集的长度,求最大总价值
不存在两个集合的价值都为空
因为我们可以把一个空集里面的线段只留下1条,其他的放在另一个空集里面
只有一个空集:把前k-1长的线段拿出来(取)
没有空集:
一个性质:
如果有一条线段包含另一条线段,则他们放在同一个集合里面,不对答案有影响
所以只考虑不被任何一条线段包含的线段
按照左端点排序,然后右端点也是递增的(因为只考虑哪些不包含别的线段的线段,如果右端点不递增,就说明里面有包含别的线段的线段)
然后就可以dp了???
一个集合里的线段应该是连续的一段线段构成的
dp[i][j]:前i条线段分成j组的最大贡献(集合里的线段是连续的)

dp[i][j]=max(dp[x][j-1]+r[x+1]-l[i])(r[x+1]>l[i])
可以单调队列优化......
stdの神仙代码:
#include<cstdio> #include<cmath> #include<cstring> #include<cstdlib> #include<algorithm> #include<functional> using namespace std; const int N=6006; typedef long long ll; const ll inf=5e13; int n,m,k,len_n,r; ll len[N],ans,dp[2][N]; struct aa { int L,R; }t1[N],t2[N]; bool cmp(aa a,aa b) { if (a.R==b.R) return a.L>b.L; return a.R<b.R; } int q[N],H,T; int main() { freopen("C.in","r",stdin); freopen("C.out","w",stdout); scanf("%d%d",&n,&k); for (int i=1;i<=n;i++) scanf("%d%d",&t1[i].L,&t1[i].R),len[i]=t1[i].R-t1[i].L; sort(len+1,len+n+1); for (int i=0;i<k-1;i++) ans+=len[n-i]; sort(t1+1,t1+n+1,cmp); memset(len,0,sizeof(len)); int mx=0; for (int i=1;i<=n;i++) if (t1[i].L>mx) { t2[++m]=t1[i]; mx=t1[i].L; }else len[++len_n]=t1[i].R-t1[i].L;//计算被其他线段包含的小线段的长度 sort(len+1,len+len_n+1,greater<ll>()); for (int i=2;i<=n;i++) len[i]+=len[i-1]; sort(t2+1,t2+m+1,cmp);//对不包含别的线段的大线段进行排序 r=1; for (int i=1;i<=m;i++) if (t2[1].R<=t2[i].L) dp[0][i]=-inf;else dp[0][i]=t2[1].R-t2[i].L;//如果当前点和1号点隔得太远那初始值就是不合法 ans=max(ans,dp[0][m]+len[k-1]);//考虑只有一个空集的情况 for (int j=2;j<=min(k,m);j++,r^=1) { q[H=T=1]=1;dp[r][1]=-inf;//q数组是手写的队列,dp数组用了玄学的滚动数组优化qwq for (int i=2;i<=m;i++) { while (H<=T&&t2[q[H]+1].R<=t2[i].L) H++;//当队首+1的右端点要比当前枚举的i的左端点小的时候就弹掉,相当于保证上面的r[x+1]>l[i] if (H<=T) dp[r][i]=dp[r^1][q[H]]+t2[q[H]+1].R-t2[i].L;else dp[r][i]=-inf; while (H<=T&&dp[r^1][i]+t2[i+1].R>=dp[r^1][q[T]]+t2[q[T]+1].R) T--; q[++T]=i; } ans=max(ans,dp[r][m]+len[k-j]);//len[k-j]表示第j+1条小线段到第k条小线段的长度和 } printf("%lld ",ans); return 0; }
(至于dp的那两维枚举的啥我是不知道了)(逃
精妙的T1


打表???
一个奇怪的哈夫曼树????
啥是哈夫曼树啊
能吃吗?
不能吧.....
既然说到哈夫曼树了,就先来一棵树
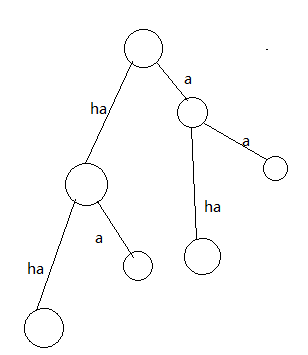
树上任何一条路径代表一个字符串
如果是前缀,就说明一个点是另一个的结尾的祖先
那字符串的数量就是叶子的数量,长度就是叶子到根的路径的长度
显然越深的路径给出现次数越少的(这货是排序不等式???)
任意一个n个叶子的数对应一个答案
显然一个节点有两个孩子比只有一个孩子要优
我们可以从根开始找孩子
设计构造树的dp(左子树深度+2,右子树深度+1)
我们可以让某一个节点不让它继续长孩子,然后这就是一个字符串了
dp[i][x][y][k]:设到了第i层,上一层的芽(可以继续长孩子的节点)有x个,这一层有y个节点,i层之前有k个叶子
i:要知道深度,所以要记录深度
长叶子的时候一根是+2的,一根是+1的,所以要记录两层(x,y))
枚举i层有多少芽成了叶子
如果有p个叶子,则代价为i*(sum[k+p]-sum[k]),sum[i]为前i个的出现次数)
dp[i][x][y][k]=max{i*(sum[k+p]-sum[k])+dp[i+1][y+x-p][x-p][k+p]}
dp[i+1][y+x-p][x-p][k+p]就是长了p个叶子之后的状态
why???
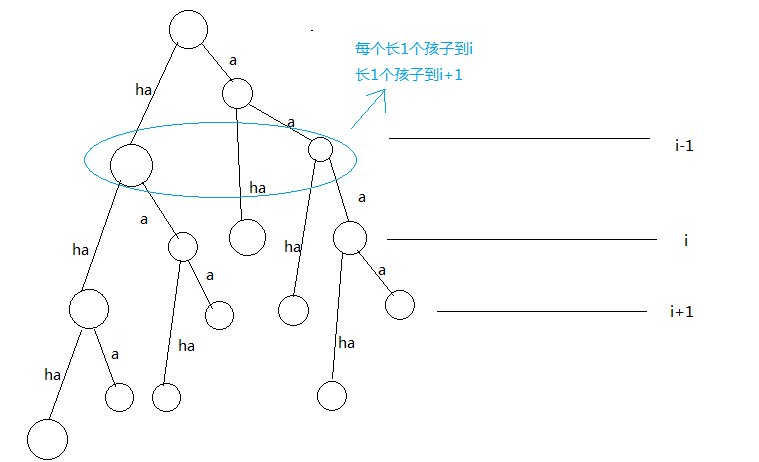
因为当前只考虑i-1层
蛤?为什么第三维没有y?
窝也不造
复杂度:O(n5)
妈耶我炸了
考虑每层的贡献
第一层:sum*n
第i层的贡献就是第i层之后的叶子的数量
既然搞出来了贡献,那是不是就不用记录深度了呢?
所以第一维没了
变成了dp[x][y][k](x是当前的芽,y是下一层的芽,k是之前的叶子)
dp[x][y][k]=min{dp[x+y-p][x-p][k+p]+sum[n]-sum[k+p]}
长出了p个叶子,剩下了sum[n]-sum[k+p]的叶子,剩下的每个叶子都要经过第i层,产生的代价就是sum[n]-sum[k+p]
复杂度O(n4)
还能优化吗?
考虑这些维和p
emmmmm还是去搞p吧,维度搞掉就逗了
可以每次让y-1,当我不想长叶子的时候就全部是芽,
转移过后:
①:长一个叶子:dp[x-1][y][k+1](就是让一个芽变成了叶子,不往下走)
②:我不想长叶子,继续往下长:dp[x+y][x][k]+sum[n]-sum[k](因为往下走了一层,所以要统计对答案的贡献)
stdの神仙code(中日英三文![]() )
)
#include<cstdio> #include<cstring> #include<cstdlib> #include<algorithm> #include<cmath> #include<map> #include<cassert> using namespace std; const int N=755; typedef unsigned int uint; const uint inf=(1u<<31)-1; uint n,a[N],sum[N]; bool cmp(uint x,uint y) {return x>y;} uint dp[2][N][N];int r; int main() { freopen("A.in","r",stdin); freopen("A.out","w",stdout); scanf("%u",&n); //assert(3<=n && n<=750); for (int i=1;i<=n;i++) scanf("%u",&a[i]),assert(1<=a[i] && a[i]<=100000); sort(a+1,a+n+1,cmp); for (int i=1;i<=n;i++) sum[i]=sum[i-1]+a[i]; for (int x=0;x<N;x++) for (int y=0;y<N;y++) dp[0][x][y]=dp[1][x][y]=inf;//dp数组神滚动优化 dp[r=0][0][0]=0; for (int k=n-1;k>=0;k--) //枚举还剩下多少个叶子没有长 { for (int y=n-k;y>=0;y--)//上文的x for (int x=n-k-y;x>=0;x--)//上文的y dp[r^1][x][y]= min(inf,x==0&&y==0?inf: min( y==0?inf:dp[r][x][y-1], x+y+y+k>n?inf:sum[n]-sum[k] + dp[r^1][y][x+y] ) ); /* for (int x=0;x<=n-(k+1);x++) for (int y=0;y<=n-(k+1)-x;y++) dp[r][x][y]=inf;*/ r^=1; } printf("%u ",sum[n]+dp[r][1][1]); return 0; }
以及充(wo)满(bu)套(hui)路(da)的T2


这里我们不确定的就是最终的各位数字之和
所以我们要枚举和!!!
边界条件:now==0&&k(%枚举的和的余数)==0&&当前各个数位之和为枚举的和:返回1,now==0但不满足上述条件返回0
代代代代码(from std)

#include<cstdio> #include<cmath> #include<cstdlib> #include<algorithm> #include<cstring> using namespace std; typedef long long ll; ll A,B; int C; int a[70],na,b[70],nb,p[70]; int mod; ll f[70][400][400]; ll query(int *a,int i,int sum,int rest,bool o) //放到a数组里,i是填到第几位,sum为当前枚举的和-当前数字各个位数之和,rest为各位之和%当前枚举的和,o是是否顶上界 { if (sum<0) return 0; if (i==0) return sum==0&&rest==0 ? 1:0; if (!o&&f[i][sum][rest]!=-1) return f[i][sum][rest]; ll ans=0; int up=o ? a[i] : C-1; for (int j=0;j<=up;j++) ans+=query(a,i-1,sum-j,(rest+mod-j*p[i]%mod)%mod,o&&j==up); if (!o) f[i][sum][rest]=ans; return ans; } int main() { freopen("B.in","r",stdin); freopen("B.out","w",stdout); scanf("%lld%lld%lld",&B,&A,&C); B--; while (A) a[++na]=A%C,A/=C; while (B) b[++nb]=B%C,B/=C; //printf("na=%d ",na); memset(f,-1,sizeof(f)); ll ans=0; for (int i=1;i<=na*C;i++) { mod=i; p[1]=1; for (int j=2;j<=na;j++) p[j]=p[j-1]*C%mod; ans+=query(a,na,mod,0,true)-(nb==0 ? 0:query(b,nb,mod,0,true)); for (int x=0;x<=na;x++) for (int y=0;y<=i;y++) for (int z=0;z<=mod;z++) f[x][y][z]=-1; } printf("%lld",ans); return 0; }
