图论

还有仙人掌神马的
关注:图的bfs,dfs
会在奇怪的题目里面起到一些作用
先来到题冷静冷静

图的重要的性质:图的dfs树只有返祖边没有横叉边
why??如果有横叉边,则dfs树的形态就会改变
非树边:原图上的不在dfs树上的边
for example
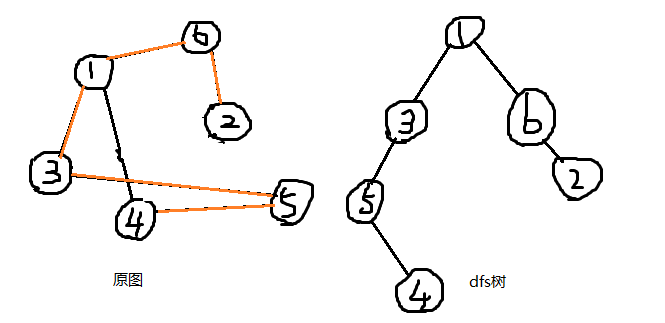
原图中橙色的是树边,而1-4这条边就是非树边
那和这道题有神马联系呢?
我们可以给这些齿轮定一些规矩,从dfs树的根节点开始计算每个点的权值(它父亲的权值*传动比),设根节点的权值为1
再枚举每个点的非树边,按照非树边的传动比再计算点的权值,如果有不一样的点,就说明不能够转动。
五行解决LCA

当然这里没有预处理深度,p数组
预处理如下:
void dfs(int son,int fa) { dep[son]=dep[fa]+1; for(int i=1;(1<<i)<=dep[son];i++)//先处理p数组 p[son][i]=p[p[son][i-1]][i-1]; for(int i=head[son];i;i=edge[i].nxt)//遍历该点的出边 { if(edge[i].to==fa)continue;//注意由于是无向图,所以要判断是不是爹 p[edge[i].to][0]=son; dfs(edge[i].to,son); } }
基础算法
最短路
一:单源最短路
一般用dijkstra(堆优化),spfa(spfa可以处理负边权,判断负环)
dijkstra(带堆优化):用来解决没有负边权的问题
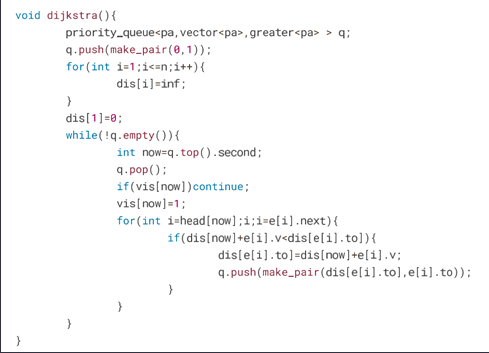
spfa

这里用了循环队列
其实这是最长路qwq
最短路只要把">"改成"<"就好辣
spfa判负环:一个点进队列超过n次
二.多源最短路
floyed(n<=500)
可以求两两之间的最短路

k是枚举中间点
其实是个dp辣
最小生成树
我们用kruskal(prim一般用不到辣)

按照边权从小到大排序,每次看边权最小的那条边,如果这条边连接的两个点不在同一个联通块中,就选这条边
查询两个点是否在一个联通块里:并查集
拓扑排序
每次选取入度为0的点删除,并且将它所到的点入度-1
用途:动态规划,判环

接下来就是让人脑仁疼的做题了
其实图论就是消耗99%的脑细胞想怎么建图,再消耗剩下的脑细胞默写最短路算法
然后脑细胞就没了ρωρ

仔细一看:最大值最小问题!!!
当然是二分辣
那问题来了,怎么检查呢?
我们可以把边权比当前的mid大的,设为1,比mid小的设为0,然后跑一遍最短路,看最短路是否小于等于K即可
繁忙的都市

直接kruskal
因为最小生成树最大边权最小
改造路

我们发现与上上道题出奇的像
but........
这里要求的是最短路的和,不是最大值啊
绞尽脑汁....没有思路.....不会....怎么办.......
图论重点:如何建图,拓扑序是什么
我们有k次免费机会,那我们不妨建k层图,每向上走一层,代表使用一次免费机会
举个栗子

这是原图
我们像下面这样建图
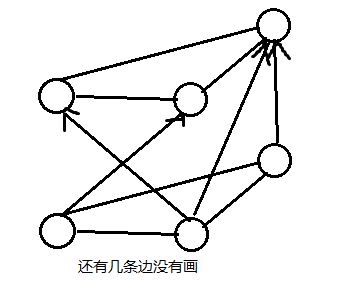
没错就是分层建图,注意这里下层向上层连边是有向边,代表使用一次免费机会,边权是0
k是多少就建多少层
最后再跑一遍dij计算最底下的1号点到最上面的N号点的最短路
显然这种东西怎么看怎么不好写
那它不好写在哪了呢?
点的编号就是个大问题的说。
我们不妨设想我们有一个棋盘
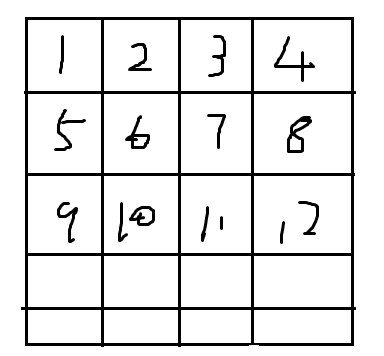
这个棋盘的列就是总节点数,棋盘的行就是层数,里面的数就是我们建图是的节点编号
我们不难发现,第i层第j个节点的编号就是(i-1)*n+j(肉眼观察得,莫得证明)
代码:
#include<bits/stdc++.h> #define ll long long using namespace std; inline int read() { char ch=getchar(); int x=0;bool f=0; while(ch<'0'||ch>'9') { if(ch=='-')f=1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); } return f?-x:x; }//快读 int n,m,k,head[2000009],cnt;//数组一定要开够,不然紫一半 struct Ed { int to,dis,nxt; }edge[20000009]; void add(int fr,int to,int dis) { cnt++; edge[cnt].to=to; edge[cnt].dis=dis; edge[cnt].nxt=head[fr]; head[fr]=cnt; } int dis[2000009]; priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >q;//转小根堆 bool vis[2000009]; void dij()//跑dijkstra(带堆优化) { q.push(make_pair(0,1)); memset(dis,0x3f,sizeof(dis)); dis[1]=0; while(!q.empty()) { int now=q.top().second; q.pop(); if(vis[now])continue; vis[now]=1; for(int e=head[now];e;e=edge[e].nxt) { if(dis[now]+edge[e].dis<dis[edge[e].to]) { dis[edge[e].to]=dis[now]+edge[e].dis; q.push(make_pair(dis[edge[e].to],edge[e].to)); } } } } int main() { n=read(),m=read(),k=read(); for(int i=1;i<=m;i++) { int fr=read(),to=read(),dis=read(); for(int j=1;j<=k+1;j++)//因为本来有1层,要向上建k层,所以一共是k+1层 { add((j-1)*n+fr,(j-1)*n+to,dis);//在当前层上建边 add((j-1)*n+to,(j-1)*n+fr,dis); add((j-1)*n+fr,j*n+to,0);//当前层向高一层建边 add((j-1)*n+to,j*n+fr,0); } } int ans=214748364; dij(); for(int i=1;i<=k+1;i++)//注意这里k次机会不一定全用完,所以是在k层中找一条最短的路线 ans=min(ans,dis[n*i]); printf("%d",ans); }
类似的题:P4568飞行路线
虫洞

在这里,我们把虫洞当做是负边权,我们如果有负环,那我们就像回到什么时候,就回到什么时候(这里强大的Farmer John无视了相对论)
spfa可以判负环,那就直接去跑spfa就好了辣
Meeting

中文版蒟蒻翻译:
奶牛Bessie和奶牛Elsie想要聚在一起,但是Farmer Jonh把草场分成了几个街区,同一街区内的点可以在ti的时间互相到达,不同街区的点不能直接走过去,但是两个街区会有交集,可以通过交集的点实现街区之间的互相到达。Bessie在第一个街区,Elsie在第n个街区,有农场地图,她们想知道她们在哪个街区汇合花费的时间最短
错误建图:同一个街区的点两两建边
正确建图:将一个街区里的所有点都连到一个新点上去,原有的点到新点的边权为ti,新点到原有的点的边权是0,这样一次来回就是ti
然后我们跑两遍最短路,一遍bessie,一遍elsie

在树上从一个点到达多的个点,按照dfs序走总是最优的(肉眼观察得(我瞎了))
我们想到求树上两个点的最短路径可以用lca,那我们两两之间求lca.
插入节点:
比如我们有4,9,12,14,我们要插入dfs序为10的节点,那就是4,9,10,12,14
对答案的贡献:-9~12最短路。+9~10最短路,+10~12最短路
删除:
就是把插入反过来辣
所以插入节点要找前驱&后继,我们可以用平衡树实现(或者是STL的set)

弹射装置的距离是曼哈顿距离

emm说形象点吧
既然是用弹弓弹射,肯定人会飞起来吧,那我们让点也飞起来

一个点花费了Ai,j的代价,升到了Bi,j的高度。当然如果想刚升上去就下来,还得有向下的边
我们还得往别的方向飘对不对
因为有重力(雾),所以每次向旁边飘一格,高度就会下降1
然后就是这样建边辣
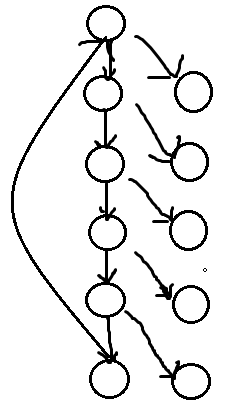
计算编号的推理方式和上面的那道分层建图差不多
然后我们跑3遍最短路(因为有3个人)就完事了
无向图性质:只有返祖边,没有横叉边
Tarjan
强连通分量:
一个图里的极大强连通子图
强连通:可以互相到达
强连通子图:一个图里的强连通的子图
强联通分量缩点

我们缩完点后还是要正常的跑最短路算法什么的,这时候怎么办呢?
我们把每个强连通分量缩成了一个点,再跑一遍原来的邻接表,如果有一条边的起点和终点不在同一个强连通分量内,就在新图中连上这条边


我们不妨缩成一个点
缩成一个点之后,看所有点,哪些出度为0.
如果有>1个点出度为0,则证明有两块牛互相不服,此时没有牛最受欢迎
如果等于1,就是那个出度为0的点所代表的强连通分量里面的牛是最受欢迎的
那么强连通分量怎么求?
我们先对有向图进行dfs.
我们给每一个点一个dfn和low
dfn代表这个点是第几步被遍历到的(时间戳)
low代表这个点的出边以及他的子树能到达的最小点的dfn(因为有返祖边的存在,所以一个点可能会有出边到达自己的祖先)
当出现横叉边的时候,尤其要注意如果这个点没有子树,只有出边,那low就是横叉边指向的那个点的dfn
如果一个强连通分量被拿走了,我们就要更新low是这个强连通分量的点的low
tarjan缩点代码:
void tarjan(int u){ dfn[u]=++ind; low[u]=dfn[u]; s[top++]=u; in[u]=1; for(int i=head[u];i;i=e[i].next){ int v=e[i].to; if(dfn[v]==0){//没遍历到 tarjan(v); low[u]=min(low[u],low[v]); }else{//遍历到了,v不在子树里面 if(in[v]){//如果v在栈里面(是u的一个祖先) low[u]=min(low[u],dfn[v]); } } } if(dfn[u]==low[u]){//发现了一个强连通分量的跟 cnt_scc++; while(s[top]!=u){//不断弹出 top--; in[s[top]]=0; scc[s[top]]=cnt_scc;//缩成一个点之后点的编号 } } }
最受欢迎的牛代码:
#include<bits/stdc++.h> #define ll long long using namespace std; inline int read() { char ch=getchar(); int x=0;bool f=0; while(ch<'0'||ch>'9') { if(ch=='-')f=1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); } return f?-x:x; } int n,m,head[10009],cnt,out[10009]; struct Ed{ int to,nxt,fr; }edge[50009]; int co[10009],sum,top,all[10009],stac[10009];//tarjan用的一些东西 int dfn[10009],low[10009],tim; bool ins[10009]; void tarjan(int u) { tim++;//tim就是时间戳 dfn[u]=tim; low[u]=dfn[u]; stac[++top]=u; ins[u]=1; for(int e=head[u];e;e=edge[e].nxt) { int v=edge[e].to; if(!dfn[v]) { tarjan(v); low[u]=min(low[u],low[v]); } else if(ins[v]) { low[u]=min(low[u],dfn[v]); } } if(low[u]==dfn[u]) { ++sum; do { ins[stac[top]]=0; co[stac[top]]=sum;all[sum]++;//all记录这个强连通分量里面有几个点 top--; }while(stac[top+1]!=u);//因为上面有个top--,所以在这里要加回去 } } void add(int fr,int to) { cnt++; edge[cnt].fr=fr; edge[cnt].to=to; edge[cnt].nxt=head[fr]; head[fr]=cnt; } int main() { n=read();m=read(); for(int i=1;i<=m;i++) { int a=read(),b=read(); add(a,b); } for(int i=1;i<=n;i++) if(!dfn[i])tarjan(i); int num=cnt;cnt=0; for(int i=1;i<=num;i++) { int u=edge[i].fr; int v=edge[i].to; if(co[u]!=co[v]) { out[co[u]]++; } } num=0;int ni=0; for(int i=1;i<=sum;i++) { if(out[i]==0) { ni=i;//记录是第几个强连通分量 num++; } } if(num>=2)//如果有两个以上没有出度的强连通分量,则没有牛是最受欢迎的 { printf("0"); return 0; } else printf("%d",all[ni]); }

按g升序排序,枚举每个g做最小生成树
我们发现这一定会T成dog
每次我们搞出的最小生成树与上一个的最小生成树最多有一条边不一样,所以我们考虑如何由上一棵最小生成树得到当前的最小生成树
我们先把当前这条边插进去,如果构成环,就比较环上的s。如果有一条边的s大于当前的s,就把s大的这条边拿下来,如果没有,就再把当前边拿下来。
O(m*n)
狼抓兔子

定理:平面图中的最小割是其对偶图的最短路
割:找出边的集合,使得把这些边删掉之后,源点和汇点不连通。
最小割:边权总和最小的割。
对偶图:边->点,点->边
平面图的对偶图:每一个块变点,边变成与之垂直的边
栗子:
原图:

step1:
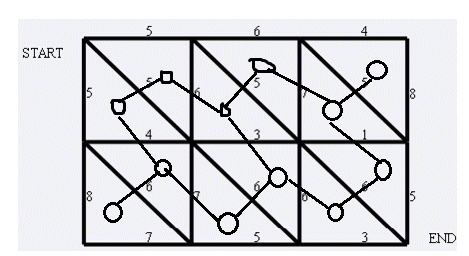
step2:我们发现这个图外面还有一个大块,我们从start到end连一条边(曲线)
然后就把外面的大块分成了一个有穷块,一个无穷块,每个块都抽象成一个点,像上面一样连边
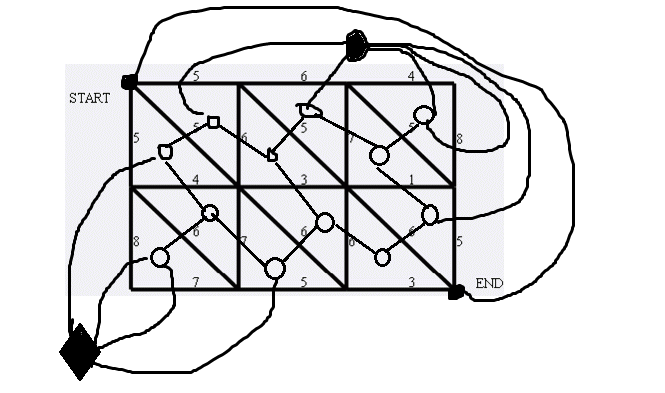
emmm最终就像这样
对偶图的边权就是原图中对应边的边权
那么菱形到右上角那个圆的最短路就是原图中的最小割(肉眼观察可得)
然后spfa走起

这是个0,1分数规划
我们发现点权这个东西很烦有木有
所以把点权移到边权上去,作为第一个边权f,原来的边权作为第二边权g
问题就是求max(∑(f)/∑(g))
令∑(f)/∑(g)≤t
∑(f)/∑(g)≤t
∑(f)≤t*∑(g)
∑(f)-∑(g)*t≤0
∑(f-g*t)≤0
二分答案+spfa验负环
最优比率生成树
还是二分t,只不过换成了求最小生成树来检验行不行(看这个最小生成树是不是负的,如果是,t就可以)

缩点+最长路
强连通分量里的钱一定可以都被抢光
所以要缩点
然后我们求个最长路(跑个spfa)
难点在于代码

点数100,边数1000000(打反了)
倍增弗洛伊德?!弗洛伊德快速幂?!
快速幂不准成精!!!(大雾)
设g1[i,j]是i到j经过1步的最短路
则g2[i,j]=min{g1[i,k],g1[k,j]}
那么g4[i,j]=min{g2[i,k],g2[k,j]}
所以gp[i,j]=min{gp/2[i,k],gp/2[k,j]}
看这像不像二进制
于是我们就可以像搞快速幂一样搞g数组了(这就是它叫弗洛伊德快速幂的原因??)
dms的代码:
while(b){ if(b&1){ memset(f,0x3f,sizeof(f));//拆一次二进制 for(int k=1;k<=n;k++){ for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ f[i][j]=min(f[i][j],ret[i][k]+g[k][j]); } } } memcpy(ret,f,sizeof(f)); } memset(f,0x3f,sizeof(f)); for(int k=1;k<=n;k++){//拆一次很可能不够,那就再拆 for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ f[i][j]=min(f[i][j],g[i][k]+g[k][j]);//由于我们有现成的g数组,就用不着二进制辽 } } } memcpy(g,f,sizeof(f)); b>>=1; } print(ret[S][E])//这是答案

注意:强连通分量只在有向图里面有

我们通过小道消息得知这些剩男和剩女之间的喜(an)欢(lian)关系
然后为了做好一个新时代的媒人,所以我们要撮合尽量多的情侣
接下来就是匈牙利算法教你如何当媒人了(雾)
我们现在有一张关系图
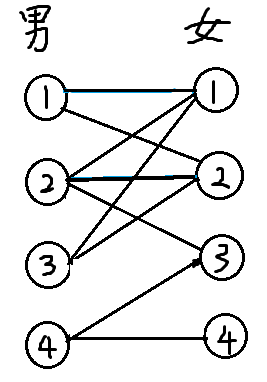
有连边代表有喜欢关系
我们先从1号男生开始考虑,发现他喜欢1号妹子,那就让他俩暂时在一起
然后发现2号男生既喜欢1号,又喜欢2号妹子,因为1号妹子已经和1号男生在一起了,所以我们让他喜欢2号妹子
现在是这个样子的(蓝色表示选了)

到了3,emmmm,发现自己来晚了,妹子都跟别人跑了,那怎么办?抢呗。
于是他抢走了1号妹子,于是触发了1号男生的大招,然后2号妹子就被1号抢走了。于是2号男生就和3号妹子幸福的在一起了
4号男生吗,就只能选4号妹子了
总结一下,就是能选就选,如果发现没有能选的了,但是别的已经有妹子的男人还可以找个别的妹子,就让那个有妹子的人赢换个妹子。
dms的代码:
int g[N][N]; int lk[N];// 妹子选了哪个男人 bool vis[N];//这一轮妹子有没有被交换 bool find(int x){ for(int i=1;i<=n;i++){ if(!vis[i]&&g[x][i]){ vis[i]=1; if(lk[i]==0||find(lk[i])){ lk[i]=x; return 1; } } } return 0; } for(int i=1;i<=n;i++){ memset(vis,0,sizeof(vis)); if(find(i)){ hunpei++; }else{ break; } }

裸的差分约束系统
一共有以下几种要求
a=b
a<=b
a<b
a>b
a>=b
如果a<b,就从a向b建一条边权为1的边
如果是等于,就从a向b建一条边权为0的边(大于等于,小于等于中的等于就是这么处理的)
如果a>b,就从b向a建一条边权为1的边
这样我们就根据差分约束建出了一张图
但是我们要满足最多的差分约束的条件,所以这里是要求最长路
代码:咕咕咕