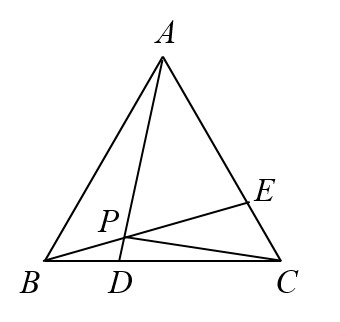
等边三角形 (ABC) 中,点 (D,E) 分别在边 (BC,AC) 上,且 (|BD|=dfrac{1}{3}|BC|,|CE|=dfrac{1}{3}|CA|,AD,BE) 相交于点 (P) . 求证: (APperp CP) .
解法一
如图,以 (BC) 边中点 (O) 为原点建立平面直角坐标系:设三角形边长为 (6) . 则 (A(0,3sqrt{3}),B(-3,0),C(3,0),D(-1,0),)(E(2,sqrt{3})) .
故直线 (AD) 的方程为$$dfrac{y-0}{3sqrt{3}-0}=dfrac{x+1}{0+1}Longrightarrow y=3sqrt{3}(x+1)$$直线 (BE) 的方程为$$dfrac{y-0}{sqrt{3}-0}=dfrac{x+3}{2+3}Longrightarrow y=dfrac{sqrt{3}}{5}(x+3)$$联立直线 (AD) 与 (BE) 的方程解得 (P(-dfrac{6}{7},dfrac{3sqrt{3}}{7})) . 而$$k_{AP}cdot k_{CP}=dfrac{3sqrt{3}-dfrac{3sqrt{3}}{7}}{0+dfrac{6}{7}}cdotdfrac{0-dfrac{3sqrt{3}}{7}}{3+dfrac{6}{7}}=-1$$所以 (APperp CP) .
解法二
设 (overrightarrow{AB}=vec{a},overrightarrow{AC}=vec{b}) ,因为 (A,P,D) 三点共线,设 (overrightarrow{AP}=moverrightarrow{AD}) , (B,P,E) 三点共线,设 (overrightarrow{BP}=noverrightarrow{BE}) ,则
又
所以
则
所以
设等边三角形的边长为 (1) ,则
所以 (overrightarrow{AP}perpoverrightarrow{CP}) ,即 (APperp CP) .