我们将一个99*99的方格表中的某些方格用特定的五种颜色之一染色,使得每种颜色都用上,且每种颜色所染的方格数相同,在每一行和每一列中,不存在染成不同颜色的方格,求至多有多少个方格被染色?
对任意一种满足题意的染色方式,都可以通过交换行或列的方式,将同一种颜色的方格“聚集”到一起,如下图所示, ABC就是三种不同颜色的聚集区,A B C区域内的方格颜色只有一种,右下角的三角形区域是未画出的区域,除了ABC和三角形区域外,其他区域都是空白区域(空白区域内格子都未被染色)。
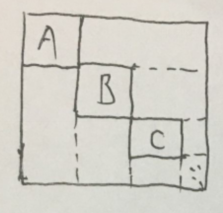
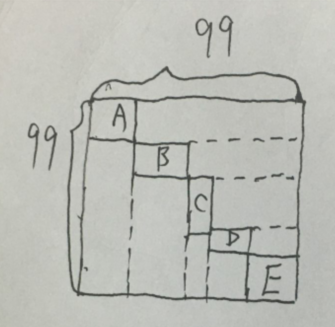
对于本题,任意符合要求的染色方式都可转化为上图的形式(右下角的E区域可以紧贴两边也可以不贴,因为在保证染色格子数量的情况下E可以改变其染色的方式且不会造成任何影响)
下面定义一种“紧凑型排列”:
紧凑型排列位于某一颜色的聚集区;紧凑型排列的第一行染色的格子数最多;除了最后一行外,其余各行的染色数都与第一行的染色数相同;染色的格子紧密相连,格子与格子之间没有空白格子;染色的格子在聚集区内靠左、靠上排列,聚集区内,所有的染色格子左侧和上侧没有空白格子;
先证明染色格子数最多的方案中一定存在某一个方案经过“聚集”操作后,五个聚集区内的排列都是紧凑型排列。
证明: 利用反证法,假设使染色格子数最多的方案中不存在一个方案经过“聚集”操作后,五个聚集区内的排列都是紧凑型排列。
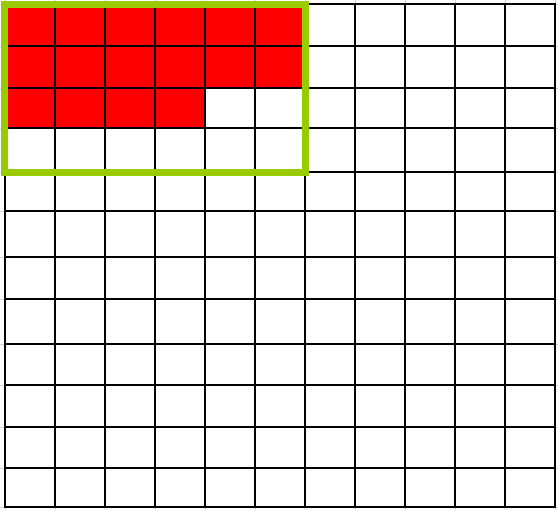
不妨设某个染色格子数最多的方案中只有一个聚集区不是紧凑型排列,且该聚集区在左上方(下图绿色框内的区域)。

可将上图这种方案变换一下变成下图这种,其他区域保持不变,此时所有的聚集区都是紧凑型排列,且这种方案的染色格子数也是最多的,假设不成立,所以染色格子数最多的方案中一定存在某一个方案经过“聚集”操作后,五个聚集区内的排列都是紧凑型排列。
令单个聚集区的行数为x,列数为y。由于交换行和列不会对染色方案有任何影响,不妨令|x-y|最小的聚集区在整个方格的左上方,|x-y|最大的聚集区在整个方格的右下方。如果聚集区的x>y,则称这个聚集区是正的, 如果x<y,则称这个聚集区是负的。下面证明当本题中的染色数最多的方案的 ∑x>94,∑y>94:
假设存在染色数最多的方案,其∑x<=94,所以至少有5列是空出来的,给5个聚集区每个区域分配一个空列,易知在空列中至少能加一个对应聚集区的颜色,所以染色的格子数还可至少+5,所以原方案不是染色数最多的方案,假设不成立,所以染色数最多的方案的∑x>94,同理可知∑y>94。
考虑这么一个问题:如果聚集区的(x+y)是定值,那么这个聚集区所包含的格子数最大是多少。 这是个很简单的问题,当(x+y)是偶数的时候,令x=y=(x+y)/2,聚集区的所包含的格子数最大,当(x+y)是奇数的时候,令x=(x+y)/2+1,y=(x+y)/2-1,或者x=(x+y)/2-1,y=(x+y)/2+1,聚集区所包含的格子数最大。
若聚集区的(x+y)=39,那么聚集区所包含的格子数最多为380个(x=20 y=19或x=19 y=20)
设本题最多可染色5n个格子,那么每种颜色的染色数为n,假设本题中的n>380,那么每个聚集区的(x+y)>39,即(x+y)>=40,那么5个聚集区的x+y>=200,由于方格表是99*99的,所以5个聚集区的x+y最多=99+99=198。所以假设不成立,所以n<=380。
当5个聚集区分别是 20*19、20*19、20*19、20*19、19*20时,n=380
所以n最大就是380,所以最多可以染色的格子数=5*n=1900