声明:本文章题目来源均为牛客网
链接:https://ac.nowcoder.com/acm/contest/884#question
A-meeting
题目类型:DFS、BFS
题目链接:https://ac.nowcoder.com/acm/contest/884/A
题目大意
给n个城市,城市与城市之间一共有n-1条边相连(就是一颗n个结点的树),然后有k个在不同城市的人(取树上的k个结点),他们决定聚在某一个城市,每走一条路所需要的时间为1,求这k个人聚到一起需要的最短时间。(n<105)
题目理解
首先距离最长的两个点肯定是最后聚在一起的,而且相聚点在这条距离最长的路中间。
求这条最长路可以先由任意一点进行DFS或BFS找出一条伪最长路,然后再由这条伪最长路的另一个端点再进行一次DFS或者BFS找到所需要的最长路,也就是找树的直径。
证明:如下图
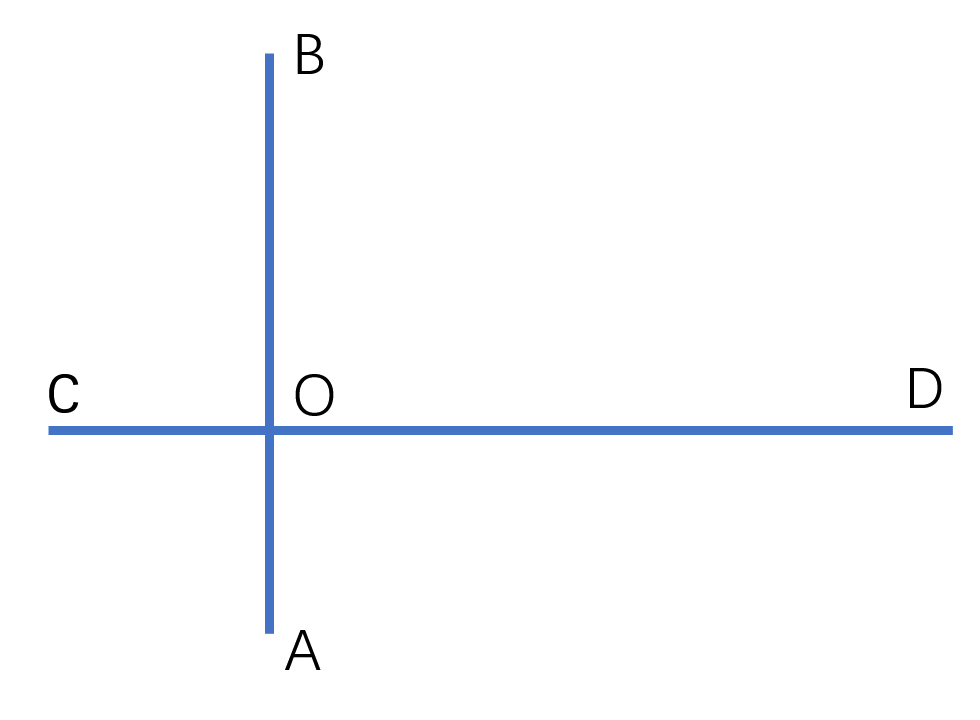
图中AO<BO,CO<DO,BO<DO
有AO+DO<DO+OB
设A点为选取的任意一点,进行DFS遍历,得到AD为伪最长路,那么再由B点DFS则BD为最长路(树的直径)。
于是此题可用两次DFS解决,最后输出(最长路+1)/2(较长的一半为最短时间)。
AC代码
#include<iostream>
#include<vector>
using namespace std;
vector<int> v[100010];
int loc[100010],ans=0,res;
void dfs(int now,int p,int len){
if(loc[now]&&len>ans){
ans=len;
res=now;
}
int y=v[now].size();
for(int i=0;i<y;i++){
int next=v[now][i];
if(next==p) continue;
dfs(next,now,len+1);
}
}
int main(){
int n,k;
cin >> n >> k;
for(int i=0;i<n-1;i++){
int v1,v2;
cin >> v1 >> v2;
v[v1].push_back(v2);
v[v2].push_back(v1);
}
while(k--){
int x;
cin >> x;
loc[x]=1;
}
dfs(1,1,0);
dfs(res,res,0);
cout << (ans+1)/2;
return 0;
}
后记
题目考察树的直径,平时做树的题目较少,而且比赛的时候没有仔细读题与思考,导致签到题都没做。
B-xor
爆肝中~
C-sequence
题目类型:分治、线段树
题目链接:https://ac.nowcoder.com/acm/contest/884/C
题目大意
有两个有n个元素的数组a和数组b,求一个[ l,r ]的区间,使得a数组元素在此区间的最小值乘上b数组在此区间的元素之和所得的数最大。
(n < 3e6,-1e6 < ( ai,bi ) < 1e6)(1 <= l <= r <= n)
题目理解
对于每一个元素a[ i ],找到它左边第一个比它小的元素a[ l ],找到右边第一个比它小的元素a[ r ],那么区间[l+1, r-1]的min就为a[ i ]。
可以用单调栈来求每个元素的区间。
将a[ i ]看作min求答案,设sum[ i ]为b数组前缀和:
- 如果a[ i ] > 0,则要最大化sum[l , r],也就是找到区间[i,r-1]的最大的sum,找到区间[l,i-1]的最小的sum,二者相减乘上a[ i ],找最大值即可;
- 如果a[ i ]<0,则要最小化sum[l , r],也就是找到区间[i,r-1]的最小的sum,找到区间[l,i-1]的最大的sum,二者相减乘上a[ i ],找最大值即可。
查询区间最值用st表和线段树都可以。
AC代码
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
using namespace std;
typedef long long LL;
const int N = 4000005;
int n;
LL a[N], b[N], L[N], R[N];
LL mx[N<<2], mn[N<<2], sum[N];
void calc(){
stack<int> st;
a[0] = a[n + 1] = -INF;
st.push(0);
for(int i = 1; i <= n; i ++){
while(!st.empty() && a[st.top()] >= a[i]) st.pop();
L[i] = st.top();
st.push(i);
}
while(!st.empty()) st.pop();
st.push(n + 1);
for(int i = n; i >= 1; i --){
while(!st.empty() && a[st.top()] >= a[i]) st.pop();
R[i] = st.top();
st.push(i);
}
}
void push_up(int rt){
mx[rt] = max(mx[rt << 1], mx[rt << 1 | 1]);
mn[rt] = min(mn[rt << 1], mn[rt << 1 | 1]);
}
void buildTree(int rt, int l, int r){
if(l == r){
mx[rt] = mn[rt] = sum[l];
return;
}
int mid = (l + r) >> 1;
buildTree(rt << 1, l, mid);
buildTree(rt << 1 | 1, mid + 1, r);
push_up(rt);
}
LL queryMax(int rt, int l, int r, int ql, int qr){
if(l == ql && r == qr){
return mx[rt];
}
int mid = (l + r) >> 1;
if(qr <= mid) return queryMax(rt << 1, l, mid, ql, qr);
else if(ql > mid) return queryMax(rt << 1 | 1, mid + 1, r, ql, qr);
else return max(queryMax(rt << 1, l, mid, ql, mid), queryMax(rt << 1 | 1, mid + 1, r, mid + 1, qr));
}
LL queryMin(int rt, int l, int r, int ql, int qr){
if(l == ql && r == qr){
return mn[rt];
}
int mid = (l + r) >> 1;
if(qr <= mid) return queryMin(rt << 1, l, mid, ql, qr);
else if(ql > mid) return queryMin(rt << 1 | 1, mid + 1, r, ql, qr);
else return min(queryMin(rt << 1, l, mid, ql, mid), queryMin(rt << 1 | 1, mid + 1, r, mid + 1, qr));
}
int main(){
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
for (int i = 1; i <= n; i++) {
scanf("%lld", &b[i]);
sum[i] = sum[i-1]+b[i];
}
calc();
buildTree(1, 0, n);
LL ans = 0;
for(int i = 1; i <= n; i ++){
int pl = L[i], pr = i - 1;
int sl = i, sr = R[i] - 1;
if(a[i] < 0){
ans = max(ans, 1LL * a[i] * (queryMin(1, 0, n, sl, sr) - queryMax(1, 0, n, pl, pr)));
}
else if(a[i] > 0){
ans = max(ans, 1LL * a[i] * (queryMax(1, 0, n, sl, sr) - queryMin(1, 0, n, pl, pr)));
}
}
printf("%lld
", ans);
return 0;
}
后记
4场比赛都用到了单调栈,多做点类似的题这题也能很容易想到办法
D-triples I
题目类型:按位或运算,思维
题目链接:https://ac.nowcoder.com/acm/contest/884/D
题目大意
输入T个数,每个数都能由3的倍数按位或得来,对于输入的数a,输出任意一组3的倍数,这些数的按位或的结果等于a。(1 < T < 1e5,1 < a < 1e18)
题目理解
一个简单的数字构造题。对于一个数a,a模上3的结果只可能为0、1、2。
如果为0,则输出a即可;
如果不为0,则将其转化为二进制。比如样例中的7,将7写成二进制,为111,其二进制每一位代表的数字模3为121(4%3=1,2%3=2,1%3=1),
得规律:如果二进制位1所在位置为奇数位,则模3为1,偶数位则为2。
- 如果a%3=1。如果a的二进制有两个及以上的奇数位的1,假设b为一个奇数位的1代表的数字,再假设c为另一个奇数位的1代表的数字,按照上面所讲的规律,a-b和a-c都为3的倍数,根据按位或的性质(只要为1则为1),(a-b) | (a-c) = a。如果二进制只有一个奇数位的1,设b为这个1代表的数字,c为任意一个偶数位1所代表的数字,a-b和b+c都为3的倍数,且(a-b) | (b+c) = a。如果二进制没有奇数位的1,设b,c,d为任意3个不同的偶数位所代表的数字,a-b-c和a+b+c为3的倍数,且(a-b-c) | (b+c+d)。
- 如果a%3=2。原理和上面一样,只需要将每一步的奇偶性反过来就行了,这里就不说了。
总结:就用原来的数字a构造3的倍数,去掉模3的有余数的数就行了,而且联想一下可以发现,只需要最多两个3的倍数就可以按位或成数字a。
AC代码
#include<iostream>
#include<vector>
#define sc(x) scanf("%d",&x);
#define scll(x) scanf("%lld",&x);
using namespace std;
typedef long long ll;
int main(){
int t;sc(t);
while(t--){
ll n;scll(n);
vector<int> one,two;
for(int i=0;i<62;i++)
if((n>>i)&1){//用vector容器分别保存二进制位奇偶性不同的1的位置
if(i&1) two.push_back(i); //保存偶数位1
else one.push_back(i);//保存奇数位1
}
if(n%3==0) printf("1 %lld
",n);
else if(n%3==1){
if(one.size()>=2)
printf("2 %lld %lld
",n-(1LL<<one[0]),n-(1LL<<one[1]));
else if(one.size()==1)
printf("2 %lld %lld
",n-(1LL<<one[0]),(1LL<<two[0])+(1LL<<one[0]));
else
printf("2 %lld %lld
",n-(1LL<<two[0])-(1LL<<two[1]),(1LL<<two[0])+(1LL<<two[1])+(1LL<<two[2]));
}else if(n%3==2){
if(two.size()>=2)
printf("2 %lld %lld
",n-(1LL<<two[0]),n-(1LL<<two[1]));
else if(two.size()==1)
printf("2 %lld %lld
",n-(1LL<<two[0]),(1LL<<two[0])+(1LL<<one[0]));
else
printf("2 %lld %lld
",n-(1LL<<one[0])-(1LL<<one[1]),(1LL<<one[0])+(1LL<<one[1])+(1LL<<one[2]));
}
}
return 0;
}
后记
构造题,找规律,也要看自己对位运算的理解以及运用。
j-free
题目类型:分层图最短路
题目链接:https://ac.nowcoder.com/acm/contest/884/J
题目大意
有一个非直接连接的图,n个结点,m条边,每条边有花费l,要求在可以让k条边权值为0的情况下,求s点到t点的最小花费。
(1 <= n,m <= 1e3,1 <= s,t <= n,1 <= l <= 1e6)
题目理解
一道分层图最短路模板题,把保存花费的d数组多开一维记录k次机会的信息。d[ i ][ j ]达到 i 点用了 j 次机会的最小花费。
更新信息的时候先更新同一层的(用了相同次机会)最小花费,然后再更新下一层的(再用一次机会)最小花费。
跑dijkstra最短路就行了(用优先队列维护)。
AC代码
#include<iostream> #include<vector> #include<queue> #include<cstring> using namespace std; const int inf=0x3f3f3f3f; int n,m,s,t,k,d[1010][1010]; typedef pair<int,int> P; struct node{ int to,cost; node(int a,int b){ to=a; cost=b; } }; vector<node> v[1010]; void dijkstra(int s){ memset(d,inf,sizeof(d)); d[s][0]=0; queue<P> que; que.push(P(s,0)); while(!que.empty()){ P now=que.front(); que.pop(); int u=now.first,t=now.second; for(int i=0;i<v[u].size();i++){ int x=v[u][i].to; int pay=v[u][i].cost; if(d[x][t]>d[u][t]+pay) //更新同层的最小花费 d[x][t]=d[u][t]+pay,que.push(P(x,t)); if(t<k&&d[x][t+1]>d[u][t]) //更新下一层的最小花费 d[x][t+1]=d[u][t],que.push(P(x,t+1)); } } } int main(){ cin >> n >> m >> s >> t >> k; while(m--){ int a,b,c; cin >> a >> b >> c; v[a].push_back(node(b,c)); v[b].push_back(node(a,c)); } dijkstra(s); int ans=inf; for(int i=0;i<=k;i++) ans=min(ans,d[t][i]); printf("%d",ans); return 0; }
后记
要不是出了这题我还不知道分层图这个东西,还是练习太少的锅。