昨天没时间写,今天补下。
昨天学的强连通分支,桥和割点,基本的网络流算法以及Dinic算法:
强连通分支
定义:在有向图G中,如果任意两个不同的顶点 相互可达,则称该有向图是强连通的。 有向图G的极大强连通子图称为G的强连 通分支。
有向图强连通分支的Tarjan算法
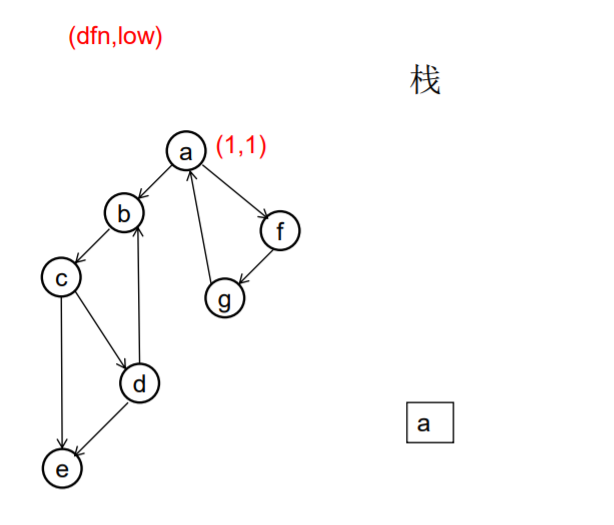
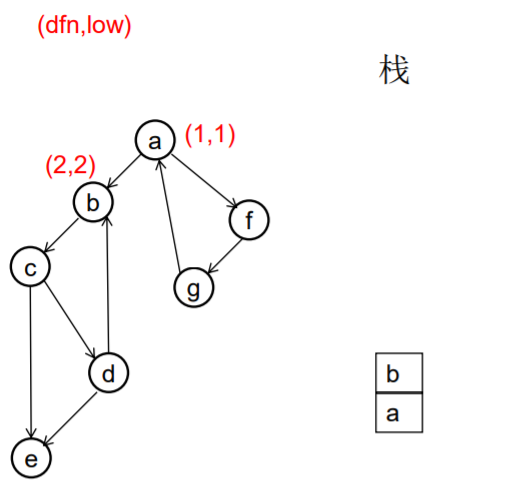
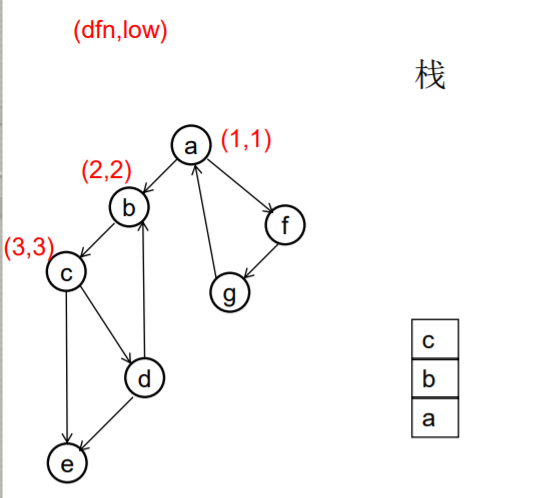
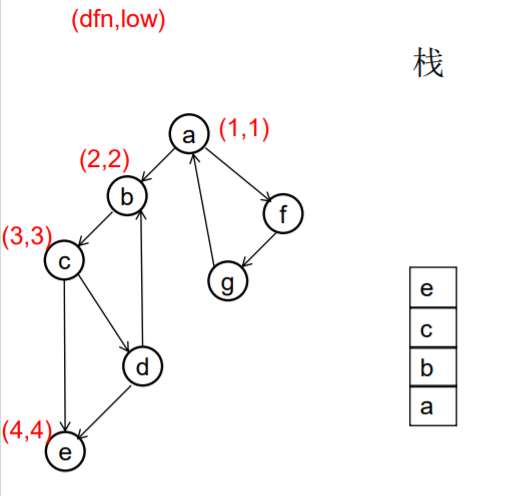
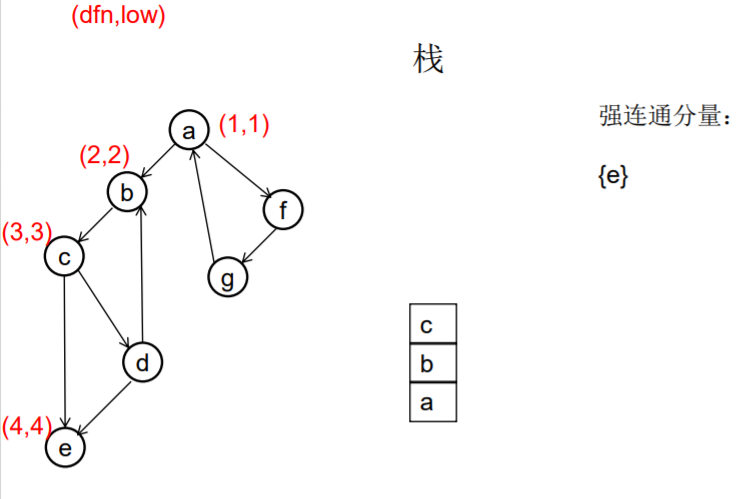
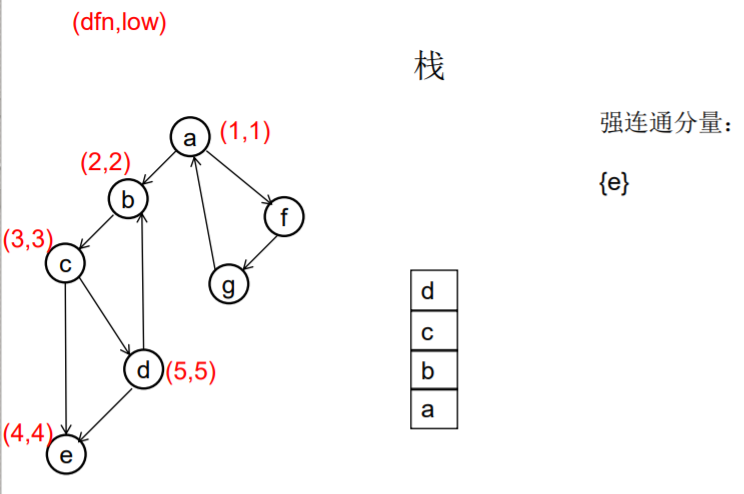
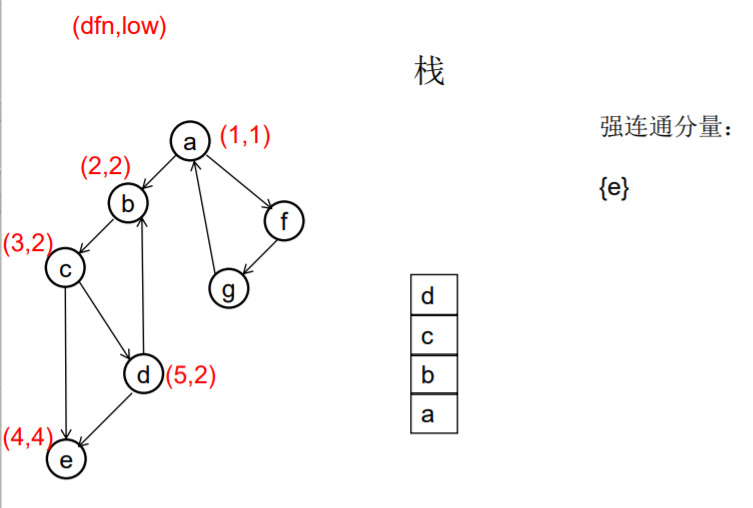
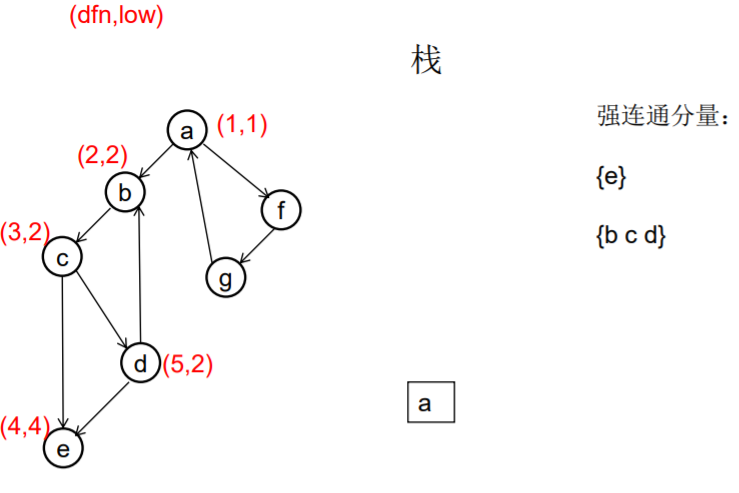
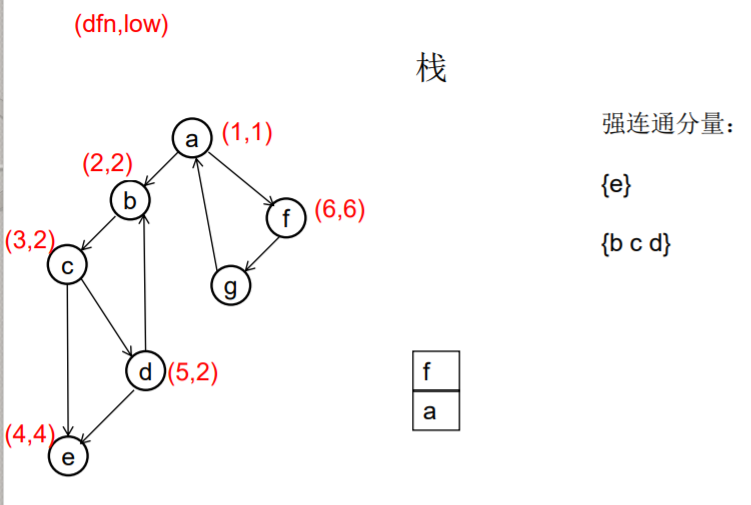
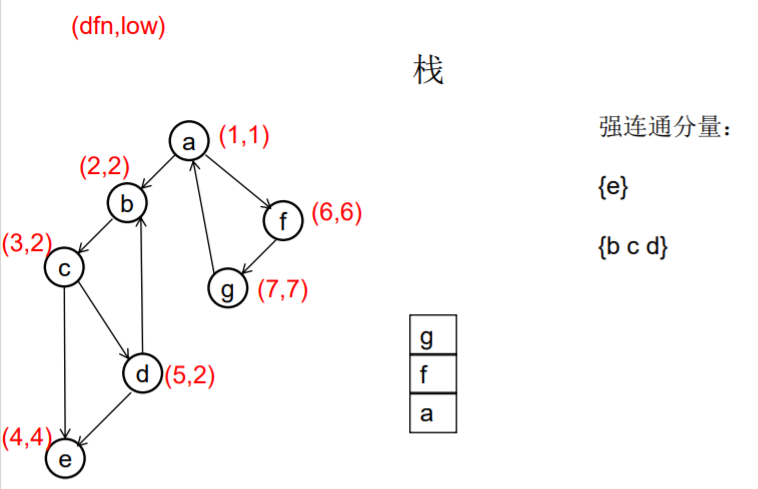
做一遍DFS,用dfn[i]表示编号为i的节点在DFS过程中的访问序号(也可以叫做开始时间)。在DFS过程中会形成一搜索树。在搜索树上越先遍历到的节点,显然dfn的值就越小。dfn值越小的节点,就称为越“早” 。
用low[i]表示从i节点出发DFS过程中i下方节点(开始时间大 于dfn[i],且由i可达的节点)所能到达的最早的节点的开始 时间。初始时low[i]=dfn[i]
DFS过程中,碰到哪个节点,就将哪个节点入栈。栈中节 点只有在其所属的强连通分量已经全部求出时,才会出栈。
如果发现某节点u有边连到栈里的节点v,则更新u的low值为min(low[u],dfn[v]) ,若low[u]被更新为dfn[v],则表明目前发现u可达的最早的节点是v。
如果一个节点u,从其出发进行的DFS已经全部完成并回到u,而且此时其low值等于dfn值,则说明u可达的所有节点,都不能到达任何比u早的节点 - --- 那么该节点u就是一个强连通分量在DFS搜索树中的根。 此时,显然栈中u上方的节点,都是不能到达比u 早的节点的。将栈中节点弹出,一直弹到u(包括u), 弹出的节点就构成了一个强连通分量。
///有向图强连通分支的Tarjan算法 ///伪代码 void Tarjan(u) { dfn[u]=low[u]=++index; stack.push(u); for each (u, v) in E { if (v is not visted) { Tarjan(v); low[u] = min(low[u], low[v]); } else if (v in stack) { low[u] = min(low[u], dfn[v]) } } if (dfn[u] == low[u]) //u是一个强连通分量的根 { repeat v = stack.pop print v until (u== v) } //退栈,把整个强连通分量都弹出来 } //复杂度是O(E+V)的
图示:
1. 2.
3. 4.
5. 6.
7. 8.

9. 10.
11. 12.
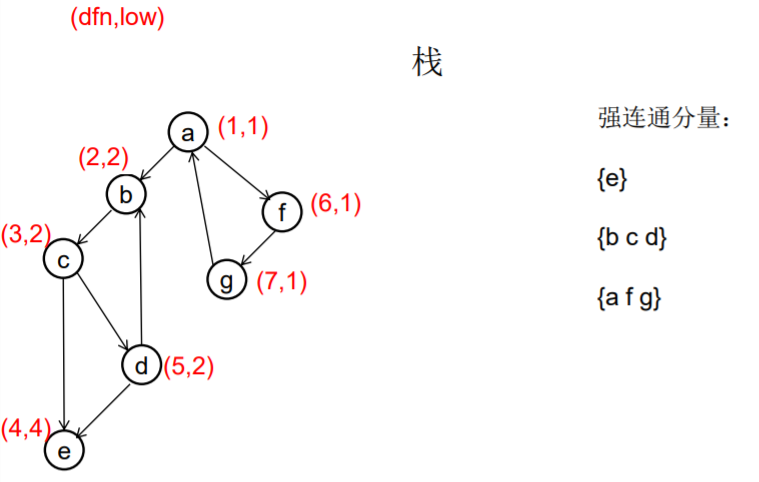
从u出发的DFS全部结束回到u时,若 dfn[u]=low[u], 此时将栈中u及其上方的节点 弹出,就找到了一个强连通分量
有用的定理:
1.有向无环图中唯一出度为0的点,一定可以由任何点出发均可达(由于无环,所以从任何点出发往前走,必然终止于一个出度为0的点)
2.有向无环图中所有入度不为0的点,一定 可以由某个入度为0的点出发可达。(由于无环,所以从任何入度不为0的点往回走,必然终止于一个入度为0的点)
例题:1.POJ 2186 Popular Cows

题目: 给定一个有向图,求有多少个顶点是由任何顶 点出发都可达的。 顶点数<= 10,000,边数 <= 50,000 思路: 1. 求出所有强连通分量。 2. 每个强连通分量缩成一点,则形成一个有向无环图DAG。 3. DAG上面如果有唯一的出度为0的点,则该点能被所有的点可达。那么该点所代表的连通分量上的所有的原图中的点,都能被原图中的所有点可达,则该连通分量的点数,就是答案。 4. DAG上面如果有不止一个出度为0的点,则这些点互相不可达,原问题无解,答案为0。 缩点的时候不一定要构造新图,只要把不同强连通分量的点染不同颜色,然后考察各种颜色的点有没有连到别的颜色的边即可(即其对应的缩点后的DAG图上的点是否有出边)。
2.POJ 1236 Network of Schools

题目大意: N(2<N<100)各学校之间有单向的网络,每个学校得到一套软件后,可以通过单向网络向周边的学校传输 问题 1:初始至少需要向多少个学校发放软件,使得网络内所有的学校最终都能得到软件。 2,至少需要添加几条传输线路(边),使任意向一个学校发放软件后,经过若干次传送,网络内所有的学校最终都能得到软件。 给定一个有向图,求: 1) 至少要选几个顶点,才能做到从这些顶点出 发,可以到达全部顶点 2) 至少要加多少条边,才能使得从任何一个顶 点出发,都能到达全部顶点 顶点数<= 100 思路: 1. 求出所有强连通分量 2. 每个强连通分量缩成一点,则形成一个有向无环图DAG。 3. DAG上面有多少个入度为0的顶点,问题1的答案就是多少 在DAG上要加几条边,才能使得DAG变成强连通的,问题2的答案就是多少 加边的方法: 要为每个入度为0的点添加入边,为每个出度为0的点添加出边 假定有 n 个入度为0的点,m个出度为0的点,max(m,n)就是第二个问题的解
无向连通图求割点和桥
割点:无向连通图中,如果删除某点后,图变 成不连通,则称该点为割点。
桥 :无向连通图中,如果删除某边后,图变 成不连通,则称该边为桥。
求桥和割点的Tarjan算法: 思路和有向图求强连通分量类似
在深度优先遍历整个图过程中形成的一棵搜索树
dfn[u]定义和前面类似,但是low[u]定义为u或者u的子树中能够通过非父子边(父子边就是搜索树上的边)追溯到的最早的节点的DFS开始时间

求桥和割点的Tarjan算法:
如果下面程序没有: if(v 不是u 的父节点) 则求不出桥了

///伪代码 Tarjan(u) { d[u]=low[u]=++index for each (u, v) in E { if (v is not visted) tarjan(v) low[u] = min(low[u], low[v]) d[u]<low[v] <==> (u, v) 是桥 } else { if(v 不是u 的父节点) low[u] = min(low[u], d[v]) } } if (u is root) u 是割点 <=> u 有至少两个子节点 else u 是割点 <=> u 有一个子节点v,满足d[u]<= low[v] }
也可以先用Tajan()进行dfs算出所有点 的low和dfn值,并记录dfs过程中每个点的父节点,然后再把所有点看一遍, 看其low和dfn,以找出割点和桥。
找桥的时候,要注意看有没有重边。有重边,则不是桥。

1 //无重边连通无向图求割点和桥的程序 2 3 /* 4 题目: 5 无重边连通无向图求割点和桥的程序 6 给出点数和所有的边,求割点和桥 7 Input: (11点13边) 8 11 13 9 1 2 10 1 4 11 1 5 12 1 6 13 2 11 14 2 3 15 4 3 16 4 9 17 5 8 18 5 7 19 6 7 20 7 10 21 11 3 22 output: 23 1 24 4 25 5 26 7 27 5,8 28 4,9 29 7,10 30 31 */ 32 33 #include <iostream> 34 #include <vector> 35 using namespace std; 36 #define MyMax 200 37 typedef vector<int> Edge; 38 vector<Edge> G(MyMax); 39 bool Visited[MyMax] ; 40 int dfn[MyMax] ; 41 int low[MyMax] ; 42 int Father[MyMax]; //DFS树中每个点的父节点 43 bool bIsCutVetext[MyMax]; //每个点是不是割点 44 int nTime; //Dfs时间戳 45 int n,m; //n是点数,m是边数 46 void Tarjan(int u, int father) //father 是u的父节点 47 { 48 Father[u] = father; 49 int i,j,k; 50 low[u] = dfn[u] = nTime ++; 51 for( i = 0; i < G[u].size() ; i ++ ) 52 { 53 int v = G[u][i]; 54 if( ! dfn[v]) 55 { 56 Tarjan(v,u); 57 low[u] = min(low[u],low[v]); 58 } 59 else if( father != v ) //连到父节点的回边不考虑,否则求不出桥 60 low[u] = min(low[u],dfn[v]); 61 } 62 } 63 void Count() 64 { 65 //计算割点和桥 66 int nRootSons = 0; 67 int i; 68 Tarjan(1,0); 69 for( i = 2; i <= n; i ++ ) 70 { 71 int v = Father[i]; 72 if( v == 1 ) 73 nRootSons ++; //DFS树中根节点有几个子树 74 else 75 { 76 if( dfn[v] <= low[i]) 77 bIsCutVetext[v] = true; 78 } 79 } 80 if( nRootSons > 1) 81 bIsCutVetext[1] = true; 82 for( i = 1; i <= n; i ++ ) 83 if( bIsCutVetext[i] ) 84 cout << i << endl; 85 for( i = 1; i <= n; i ++) 86 { 87 int v = Father[i]; 88 if(v >0 && dfn[v] < low[i]) 89 cout << v << "," << i <<endl; 90 } 91 } 92 int main() 93 { 94 int u,v; 95 int i; 96 nTime = 1; 97 cin >> n >> m ; //n是点数,m是边数 98 for( i = 1; i <= m; i ++ ) 99 { 100 cin >> u >> v; //点编号从1开始 101 G[v].push_back(u); 102 G[u].push_back(v); 103 } 104 memset( dfn,0,sizeof(dfn)); 105 memset( Father,0,sizeof(Father)); 106 memset( bIsCutVetext,0,sizeof(bIsCutVetext)); 107 Count(); 108 return 0; 109 }
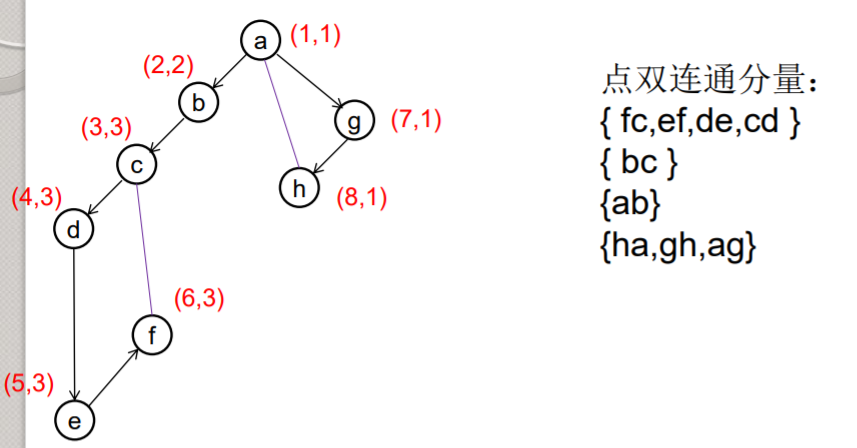
求无向图连通图点双连通分支(不包含割点的极大连通子图):
对于点双连通分支,实际上在求割点的过程中就能顺便把每个点双连通分支求出。建立 一个栈,存储当前双连通分支,在搜索图时 ,每找到一条树枝边或反向边(连到树中祖先的边),就把这条边加入栈中。如果遇到某树枝边(u,v) 满足dfn(u)<=low(v),说明u是 一个割点,此时把边从栈顶一个个取出,直到遇到了边(u,v),取出的这些边与其关联的点,组成一个点双连通分支。割点可以属于多个点双连通分支,其余点和每条边只属于且属于一个点双连通分支。

1 ///求无向连通图点双连通分量(没有割点的连通分量),假定没有重边 2 3 /* 4 Input: (8点9边) 5 8 9 6 1 2 7 1 3 8 1 5 9 3 5 10 2 4 11 4 6 12 4 7 13 6 8 14 7 8 15 output: 16 Block No: 1 17 7,4 18 8,7 19 6,8 20 4,6 21 Block No: 2 22 2,4 23 Block No: 3 24 1,2 25 Block No: 4 26 5,1 27 3,5 28 1,3 29 */ 30 31 //求无向连通图点双连通分量(没有割点的连通分量),假定没有重边 32 #include <iostream> 33 #include <cstring> 34 #include <vector> 35 #include <queue> 36 using namespace std; 37 #define MyMax 200 38 typedef vector<int> Edge; 39 vector<Edge> G(MyMax); 40 int dfn[MyMax] ; 41 int low[MyMax] ; 42 int nTime; 43 int n,m; //n是点数,m是边数 44 struct Edge2 45 { 46 int u; 47 int v; 48 Edge2(int u_,int v_):u(u_),v(v_) { } 49 }; 50 deque<Edge2> Edges; //栈 51 int nBlockNo = 0; 52 void Tarjan(int u, int father) 53 { 54 int i,j,k; 55 low[u] = dfn[u] = nTime ++; 56 for( i = 0; i < G[u].size() ; i ++ ) 57 { 58 int v = G[u][i]; 59 if( ! dfn[v]) //v没有访问过 60 {//树边要入栈 61 Edges.push_back(Edge2(u,v)); 62 Tarjan(v,u); 63 low[u] = min(low[u],low[v]); 64 Edge2 tmp(0,0); 65 if(dfn[u] <= low[v]) 66 { 67 //从一条边往下走,走完后发现自己是割点,则栈中的边一定全是和自己在一个双连通分量里面 68 //根节点总是和其下的某些点在同一个双连通分量里面 69 cout << "Block No: " << ++ nBlockNo<< endl; 70 do 71 { 72 tmp = Edges.back(); 73 Edges.pop_back (); 74 cout << tmp.u << "," << 75 tmp.v << endl; 76 } 77 while ( !(tmp.u == u && 78 tmp.v == v) ); 79 } 80 } // 对应if( ! dfn[v]) { 81 else 82 { 83 if( v != father ) //u连到父节点的回边不考虑 84 { 85 low[u] = min(low[u],dfn[v]); 86 if( dfn[u] > dfn[v]) 87 //连接到祖先的回边要入栈,但是连接到儿子的边,此处肯定已经入过栈了,不能再入栈 88 Edges.push_back(Edge2(u,v)); 89 } 90 } 91 } //对应 for( i = 0;i < G[u].size() ;i ++ ) { 92 } 93 int main() 94 { 95 int u,v; 96 int i; 97 nTime = 1; 98 cin >> n >> m ; //n是点数,m是边数 99 nBlockNo = 0; 100 for( i = 1; i <= m; i ++ ) 101 { 102 cin >> u >> v; //点编号从1开始 103 G[v].push_back(u); 104 G[u].push_back(v); 105 } 106 memset( dfn,0,sizeof(dfn)); 107 Tarjan(1,0); 108 return 0; 109 }
求无向连通图边双连通分支(不包 含桥的极大连通子图):
只需在求出所有的桥以后,把桥边删除,原图变成了多个连通块,则每个连通块就是一个边双连通分支。桥不属于任何一个边双连通分支,其余的边和每个顶点都属于且只属于 一个边双连通分支。
例题:POJ 3352 Road Construction

题目意思: 给你一个图,要求你加入最少的边,使得最后得到的图为一个边双连通分支。所谓的边双连通分支,即不存在桥的连通分支。 可以求出所有的桥,把桥删掉。然后把所有的连通分支求出来,显然这些连通分支就是原图中的双连通分支。把它们缩成点,然后添上刚才删去的桥,就构成了一棵树。在树上添边使得树变成一个双连通分支即可。 本题只要求输出一共需要添加多少条边,而不需要求具体的方案。其实可以统计度为1的叶子节点(设共有x个),然后直接输出(x+1)/2即可 命题:一棵有n(n>=2)个叶子结点的树,至少(只需)要添加ceil(n/2)条边,才(就)能转变为一个没有桥的图。或者说,使得图中每条边,都至少在一个环上。 证明: 这里只证明n为偶数的情况。n为奇数的证明类似。 先证明添加n/2条边一定可以达成目标。 n=2时,显然只需将这两个叶子间连一条边即可。命题成立。 设n=2k(k>=1)时命题成立,即AddNum(2k)=k。下面将推出n=2(k+1)时命题亦成立 n=2k+2时,选取树中一条迹(无重复点的路径),设其端点为a,b;并设离a最近的度>=3的点为a',同理设b'。(关于a‘和b’的存在性问题:由于a和b的度都为1,因此树中其它的树枝必然从迹<a,b>之间的某些点引出。否则整棵树就是迹<a,b>,n=2<2k+2,不可能。) a’ b’不重合时: 在a,b间添一条边,则迹<a,b>上的所有边都已不再是桥。这时,将刚才添加的边,以及aa‘之间,bb’之间的边都删去,得到一棵新的树。因为删去的那些边都已经符合条件了,所以在之后的构造中不需要考虑它们。由于之前a‘和b’的度>=3,所以删除操作不会使他们变成叶子。因此新的树必然比原树少了两个叶子a,b,共有2k个叶子。由归纳知需要再加k条边。因此对n=2k+2的树,一共要添加k+1条边。 a’ b’ 重合时: 将a和一个非b的叶子节点x连上,然后将环缩点至 a’。因为叶子节点是偶数,所以必然还存在一个非b非x的叶子节点不在环上, 因此a’不会变成叶子节点,于是新图比原图少2个叶子节点。 再证明n/2是最小的解。 显然,只有一个叶子结点被新加的边覆盖到,才有可能使与它相接的那条边进入一个环中。而一次加边至多覆盖2个叶子。因此n个叶子至少要加n/2条边。 证毕。
其他题目:acm1236,acm3180,acm2762(强连通+拓扑排 序),acm2553,acm3114(强连通 +dijkstra), acm3160(强连通+DP)
网络流算法
网络流图里,源点流出的量,等于汇点流 入的量,除源汇外的任何点,其流入量之 和等于流出两之和
解决最大流的Ford-Fulkerson算法
求最大流的过程,就是不断找到一条源到汇的路径,然后构建残余网络,再在残余网络上寻找新的路径,使总流量增加,然后形成新的残余网络,再寻找新路径…..直到某个残余网络上找不到从源到汇的路径为止,最大流就算出来了。
每次寻找新流量并构造新残余网络的过程, 就叫做寻找流量的“增广路径”,也叫“增 广”
残余网络:在一个网络流图上,找到一条源到汇的路径(即找到了一个流量)后,对路径上所有的边,其容量都减去此次找到的流量,对路径 上所有的边,都添加一条反向边,其容量也 等于此次找到的流量,这样得到的新图,就称为原图的“残余网络”。
为什么添加反向边(取消流)是有效的?
假设在第一次寻找流的时候,发现在b->a上 可以有流量n来自源,到达b,再流出a后抵达汇点。
构建残余网络时添加反向边a->b,容量是n,增 广的时候发现了流量n-k,即新增了n-k的流量。 这n-k的流量,从a进,b出,最终流到汇
这2n-k的从流量,在原图上可以从源流到汇
现在假设每条边的容量都是整数
这个算法每次都能将流至少增加1
由于整个网络的流量最多不超过图中所有的边的容量和C,从而算法会结束
现在来看复杂度
找增广路径的算法可以用dfs, 复杂度为边数m+顶 点数n
Dfs 最多运行C次
所以时间复杂度为C*(m+n) =C* n2
为了避免C很大时程序要执行很多次的情况,在每次增广的时候,选择从源到汇的具有最 少边数的增广路径,即不是通过dfs寻找增广路 径,而是通过bfs寻找增广路径。这就是Edmonds-Karp最短增广路算法。已经证明这种算法的复杂度上限为nm2(n是点数,m是边数)。
例题:POJ 1273 Drainage Ditches

1 /* 2 题目: 3 赤裸裸的网络流题目。给定点数,边数,每条 4 边的容量,以及源点,汇点,求最大流。 5 Sample Input 6 5 4 7 1 2 40 8 1 4 20 9 2 4 20 10 2 3 30 11 3 4 10 12 Sample Output 13 50 14 */ 15 16 #include <cstring> 17 #include <iostream> 18 #include <queue> 19 using namespace std; 20 int G[300][300]; 21 int Prev[300]; //路径上每个节点的前驱节点 22 bool Visited[300]; 23 int n,m; //m是顶点数目,顶点编号从1开始 1是源,m是汇, n是边数 24 unsigned Augment() 25 { 26 int v; 27 int i; 28 deque<int> q; 29 memset(Prev,0,sizeof(Prev)); 30 memset(Visited,0,sizeof(Visited)); 31 Prev[1] = 0; 32 Visited[1] = 1; 33 q.push_back(1); 34 bool bFindPath = false; 35 //用bfs寻找一条源到汇的可行路径 36 while( ! q.empty()) 37 { 38 v = q.front(); 39 q.pop_front(); 40 for( i = 1; i <= m; i ++) 41 { 42 if( G[v][i] > 0 && Visited[i] == 0) 43 { 44 //必须是依然有容量的边,才可以走 45 Prev[i] = v; 46 Visited[i] = 1; 47 if( i == m ) 48 { 49 bFindPath = true; 50 q.clear(); 51 break; 52 } 53 else 54 q.push_back(i); 55 } 56 } 57 } 58 if( ! bFindPath) 59 return 0; 60 int nMinFlow = 999999999; 61 v = m; 62 //寻找源到汇路径上容量最小的边,其容量就是此次增加的总流量 63 while( Prev[v] ) 64 { 65 nMinFlow = min( nMinFlow,G[Prev[v]][v]); 66 v = Prev[v]; 67 } 68 //沿此路径添加反向边,同时修改路径上每条边的容量 69 v = m; 70 while( Prev[v] ) 71 { 72 G[Prev[v]][v] -= nMinFlow; 73 G[v][Prev[v]] += nMinFlow; 74 v = Prev[v]; 75 } 76 return nMinFlow; 77 } 78 int main() 79 { 80 while (cin >> n >> m ) 81 { 82 //m是顶点数目,顶点编号从1开始 83 int i,j,k; 84 int s,e,c; 85 memset( G,0,sizeof(G)); 86 for( i = 0; i < n; i ++ ) 87 { 88 cin >> s >> e >> c; 89 G[s][e] += c; //两点之间可能有多条边 90 } 91 unsigned int MaxFlow = 0; 92 unsigned int aug; 93 while( aug = Augment() ) 94 MaxFlow += aug; 95 cout << MaxFlow << endl; 96 } 97 return 0; 98 }
Dinic 算法
Edmonds-Karp的提高余地:需要多次从s到t调用BFS,可以设法减少调用次数。
亦即:使用一种代价较小的高效增广方法。
考虑:在一次增广的过程中,寻找多条增广路径。
DFS
先利用 BFS对残余网络分层,分完层后,利用DFS从前一层向后一层反复寻找增广路(即要求DFS的每一步都必须要走到下一层 的节点)。
一个节点的“层”数,就是源点到它最少要经过的边数。
DFS过程中,要是碰到了汇点,则说明找到了一条增广 路径。此时要增加总流量的值,消减路径上各边的容 量,并添加反向边,即所谓的进行增广。
DFS找到一条增广路径后,并不立即结束,而是回溯后 继续DFS寻找下一个增广路径。
回溯到的节点u满足以下条件:
1) DFS搜索树的树边(u,v)上的容量已经变成0。即刚刚找到的增广路径上所增加的流量,等于(u,v)本次增广前的容量。(DFS的过程中,是从u走到更下层的v的) 2)u是满足条件 1)的最上层的节点
如果回溯到源点而且无法继续往下走了,DFS结束。
因此,一次DFS过程中,可以找到多条增广路径。 DFS结束后,对残余网络再次进行分层,然后再进行DFS
当残余网络的分层操作无法算出汇点的层次(即BFS到达不了汇点)时,算法结束,最大流求出。 一般用栈实现DFS,这样就能从栈中提取出增广路径。 Dinic 复杂度是 n*n*m (n是点数,m是边数)
要求出最大流中每条边的流量,怎么办?
将原图备份,原图上的边的容量减去做完最大 流的残余网络上的边的剩余容量,就是边的流量。
例题:1.POJ 1273 Drainage Ditches

1 #include <cstring> 2 #include <iostream> 3 #include <queue> 4 using namespace std; 5 #define INFINITE 999999999 //Poj 1273 Drainage Ditches 的 Dinic算法 6 int G[300][300]; 7 bool Visited[300]; 8 int Layer[300]; 9 int n,m; //1是源点,m是汇点 10 bool CountLayer() 11 { 12 int layer = 0; 13 deque<int>q; 14 memset(Layer,0xff,sizeof(Layer)); //都初始化成-1 15 Layer[1] = 0; 16 q.push_back(1); 17 while( ! q.empty()) 18 { 19 int v = q.front(); 20 q.pop_front(); 21 for( int j = 1; j <= m; j ++ ) 22 { 23 if( G[v][j] > 0 && Layer[j] == -1 ) 24 { 25 //Layer[j] == -1 说明j还没有访问过 26 Layer[j] = Layer[v] + 1; 27 if( j == m ) //分层到汇点即可 28 return true; 29 else 30 q.push_back(j); 31 } 32 } 33 } 34 return false; 35 } 36 int Dinic() 37 { 38 int i; 39 int s; 40 int nMaxFlow = 0; 41 deque<int> q; //DFS用的栈 42 while( CountLayer() ) //只要能分层 43 { 44 q.push_back(1); //源点入栈 45 memset(Visited,0,sizeof(Visited)); 46 Visited[1] = 1; 47 while( !q.empty()) 48 { 49 int nd = q.back(); 50 if( nd == m ) // nd是汇点 51 { 52 //在栈中找容量最小边 53 int nMinC = INFINITE; 54 int nMinC_vs; //容量最小边的起点 55 for( i = 1; i < q.size(); i ++ ) 56 { 57 int vs = q[i-1]; 58 int ve = q[i]; 59 if( G[vs][ve] > 0 ) 60 { 61 if( nMinC > G[vs][ve] ) 62 { 63 nMinC = G[vs][ve]; 64 nMinC_vs = vs; 65 } 66 } 67 } 68 //增广,改图 69 nMaxFlow += nMinC; 70 for( i = 1; i < q.size(); i ++ ) 71 { 72 int vs = q[i-1]; 73 int ve = q[i]; 74 G[vs][ve] -= nMinC; //修改边容量 75 G[ve][vs] += nMinC; //添加反向边 76 } 77 //退栈到 nMinC_vs成为栈顶,以便继续dfs 78 while( !q.empty() && q.back() != nMinC_vs ) 79 { 80 Visited[q.back()] = 0; //没有这个应该也对 81 q.pop_back(); 82 } 83 } 84 else //nd不是汇点 85 { 86 for( i = 1; i <= m; i ++ ) 87 { 88 if( G[nd][i] > 0 && Layer[i] == Layer[nd] + 1 && 89 ! Visited[i]) 90 { 91 //只往下一层的没有走过的节点走 92 Visited[i] = 1; 93 q.push_back(i); 94 break; 95 } 96 } 97 if( i > m) //找不到下一个点 98 q.pop_back(); //回溯 99 } 100 } 101 } 102 return nMaxFlow; 103 } 104 int main() 105 { 106 while (cin >> n >> m ) 107 { 108 int i,j,k; 109 int s,e,c; 110 memset( G,0,sizeof(G)); 111 for( i = 0; i < n; i ++ ) 112 { 113 cin >> s >> e >> c; 114 G[s][e] += c; //两点之间可能有多条边 115 } 116 cout << Dinic() << endl; 117 } 118 return 0; 119 }
2.POJ 3436 ACM Computer Factory

题目: 电脑公司生产电脑有N个机器,每个机器单位时间产量为Qi。电脑由P个部件组成,每个机器工作时只能把有某些部件的半成品电脑(或什么都没有的空电脑)变成有另一些部件的半成品电脑或完整电脑(也可能移除某些部件)。求电脑公司的单位时间最大产量,以及哪些机器有协作关系,即一台机器把它的产品交给哪些机器加工。 Sample input 3 4 15 0 0 0 0 1 0 10 0 0 0 0 1 1 30 0 1 2 1 1 1 3 0 2 1 1 1 1 Sample output 25 2 1 3 15 2 3 10 输入:电脑由3个部件组成,共有4台机器,1号机器产量15, 能给空电脑加 上2号部件,2号 机器能给空电脑加上2号部件和3号部件, 3号机器能把 有1个2号部件和3号部件有无均可的电脑变成成品(每种部件各有一个) 输出:单位时间最大产量25,有两台机器有协作关系, 1号机器单位时间内要将15个电脑给3号机器加工 2号机器单位时间内要将10个电脑给3号机器加工 建模分析: 每个工厂有三个动作: 1)接收原材料 2)生产 3)将其产出的半成品给其他机器,或产出成品。 这三个过程都对应不同的流量。 网络流模型: 1) 添加一个原点S,S提供最初的原料 00000... 2) 添加一个汇点T, T接受最终的产品 11111.... 3) 将每个机器拆成两个点: 编号为i的接收节点,和编号为i+n的产出节点(n是机器数目),前者用于接收原料,后者用于提供加工后的半成品或成品。这两个点之间要连一条边,容量为单位时间产量Qi 4) S 连边到所有接收 "0000..." 或 "若干个0及若干个2"的机器,容量为无穷大 5) 产出节点连边到能接受其产品的接收节点,容量无穷大 6) 能产出成品的节点,连边到T,容量无穷大。 7) 求S到T的最大流
3.poj 2112 Optimal Milking

题目: 有K台挤奶机器和C头牛(统称为物体),每台挤奶机器只能容纳M头牛进行挤奶。现在给出dis[K + C][K + C]的矩阵,dis[i][j]若不为0则表示第i个物体到第j个物体之间有路,dis[i][j]就是该路的长度。(1 <= K <= 30,1 <=C <= 200) 现在问你怎么安排这C头牛到K台机器挤奶,使得需要走最长路程到挤奶机器的奶牛所走的路程最少,求出这个最小值。 Sample Input 2 3 2 // K C M 0 3 2 1 1 3 0 3 2 0 2 3 0 1 0 1 2 1 0 2 1 0 0 2 0 Sample Output 2 分析: 利用Floyd算法求出每个奶牛到每个挤奶机的最短距离。 则题目变为: 已知C头奶牛到K个挤奶机的距离,每个挤奶机只能有M个奶牛,每个奶牛只能去一台挤奶机,求这些奶牛到其要去的挤奶机距离的最大值的最小值。 网络流模型: 每个奶牛最终都只能到达一个挤奶器,每个挤奶器只能有M个奶牛,可把奶牛看做网络流中的流。 每个奶牛和挤奶器都是一个节点,添加一个源,连边到所有奶牛节点,这些边容量都是1。 添加一个汇点,每个挤奶器都连边到它。这些边的容量都是M。 网络流模型: 先假定一个最大距离的的最小值 maxdist, 在上述图中,如果奶牛节点i和挤奶器节点j之间的距离<=maxdist,则从i节点连一条边到j节点,表示奶牛i可以到挤奶器j去挤奶。该边容量为1。该图上的最大流如果是C(奶牛数),那么就说明假设的 maxdist成立,则减小 maxdist再试 总之,要二分 maxdist, 对每个maxdist值,都重新构图,看其最大流是否是C,然后再决定减少或增加maxdist
