今天讲了DFA,最小生成树以及最短路
DFA(接着昨天讲)
如何高效的构造前缀指针:
步骤为:根据深度一一求出每一个节点的前缀指针。对于当前节点,设他的父节点与他的边上的字符为Ch,如果他的父节点的前缀指针所指向的节点的儿子中,有通过Ch字符指向的儿子,那么当前节点的前缀指针指向该儿子节点,否则通过当前节点的父节点的前缀指针所指向点的前缀指针,继续向上查找,直到到达根节点为止。
ps:构造前缀指针时在最前面加一个0号节点。
对于一个插入了n个模式串的单词 前缀树构造其前缀指针的时间复杂 度为:O(∑len(i)) (i=1..n)
如何在建立好的Trie图上遍历:
遍历的方法如下:从ROOT出发,按照当前串的下一 个字符ch来进行在树上的移动。若当前点P不存在通过ch连接的儿子,那么考虑P的前缀指针指向的节点Q,如果还无法找到通过ch连接的儿子节点,再考虑Q的前缀指针… 直到找到通过ch连接的儿子,再继续遍历。如果遍历过程中经过了某个终止节点,则说明S包含该终止节点代表的模式串. 如果遍历过程中经过了某个非终止节点的危险节点, 则可以断定S包含某个模式串。要找出是哪个,沿着危险节点的前缀指针链走,碰到终止节点即可。
ps: 危险节点:1) 终止节点是危险节点 2) 如果一个节点的前缀指针指向危险节点,那么它也是危险节点。
这样遍历一个串S的时间复杂度是O(len(S))
最纯粹的Trie图题目:

给N个模式串,每个不超过个字符,再给M个句子,句子长度< 100 判断每个句子里是否包含模式串 N < 10, M < 10 ,字符都是小写字母 5 8 abcde defg cdke ab f abcdkef abkef bcd bca add ab qab f

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <vector> 5 #include <queue> 6 using namespace std; 7 #define LETTERS 26 8 int nNodesCount = 0; 9 struct CNode 10 { 11 CNode * pChilds[LETTERS]; 12 CNode * pPrev; //前缀指针 13 bool bBadNode; //是否是危险节点 14 void Init() 15 { 16 memset(pChilds,0,sizeof(pChilds)); 17 bBadNode = false; 18 pPrev = NULL; 19 } 20 }; 21 CNode Tree[200]; //10个模式串,每个10个字符,每个字符一个节点,也只要100个节点 22 23 void Insert( CNode * pRoot, char * s) 24 { 25 //将模式串s插入trie树 26 for( int i = 0; s[i]; i ++ ) 27 { 28 if( pRoot->pChilds[s[i]-'a'] == NULL) 29 { 30 pRoot->pChilds[s[i]-'a'] =Tree + nNodesCount; 31 nNodesCount ++; 32 } 33 pRoot = pRoot->pChilds[s[i]-'a']; 34 } 35 pRoot-> bBadNode = true; 36 } 37 void BuildDfa( ) 38 { 39 //在trie树上加前缀指针 40 for( int i = 0; i < LETTERS ; i ++ ) 41 Tree[0].pChilds[i] = Tree + 1; 42 Tree[0].pPrev = NULL; 43 Tree[1].pPrev = Tree; 44 deque<CNode * > q; 45 q.push_back(Tree+1); 46 while( ! q.empty() ) 47 { 48 CNode * pRoot = q.front(); 49 q.pop_front(); 50 for( int i = 0; i < LETTERS ; i ++ ) 51 { 52 CNode * p = pRoot->pChilds[i]; 53 if( p) 54 { 55 CNode * pPrev = pRoot->pPrev; 56 while( pPrev ) 57 { 58 if( pPrev->pChilds[i] ) 59 { 60 p->pPrev = pPrev->pChilds[i]; 61 if( p->pPrev-> bBadNode) 62 p-> bBadNode = true; 63 //自己的pPrev指向的节点是危险节点,则自己也是危险节点 64 break; 65 } 66 else 67 pPrev = pPrev->pPrev; 68 } 69 q.push_back(p); 70 } 71 } 72 } //对应于while( ! q.empty() ) 73 } 74 bool SearchDfa(char * s) 75 { 76 //返回值为true则说明包含模式串 77 CNode * p = Tree + 1; 78 for( int i = 0; s[i] ; i ++ ) 79 { 80 while(true) 81 { 82 if( p->pChilds[s[i]-'a']) 83 { 84 p = p->pChilds[s[i]-'a']; 85 if( p-> bBadNode) 86 return true; 87 break; 88 } 89 else 90 p = p->pPrev; 91 } 92 } 93 return false; 94 } 95 int main() 96 { 97 nNodesCount = 2; 98 int M,N; 99 scanf("%d%d",&N,&M); //N个模式串,M个句子 100 for( int i = 0; i < N; i ++ ) 101 { 102 char s[20]; 103 scanf("%s",s); 104 Insert(Tree + 1,s); 105 } 106 BuildDfa(); 107 for( int i = 0 ; i < M; i ++ ) 108 { 109 char s[200]; 110 scanf("%s",s); 111 cout << SearchDfa(s) << endl; 112 } 113 return 0; 114 }
PS:有可能模式串A是另一模式串B的子串,此情况下可能只能得出匹配B的结论而忽略也匹配A,所以不能只看终止节点,还要看危险节点:
对每个节点设置一个“是否计算过”的标记,当标记一个危险节点为“已匹配”时,沿该节点对应的S的所有后缀指针一直到根节点全标记为“已匹配”。
例题:1.POJ3987 Computer Virus on Planet Pandora 2010 福州赛区题目
2.POI #7 题:病毒
3.POJ 3691 DNA repair
4.POJ 1625 Censored!
5.POJ2778 DNA Sequence
最小生成树(MST)问题
生成树:
1.无向连通图的边的集合
2.无回路
3.连接所有的点
最小: 所有边的权值之和最小
有n个顶点,n-1条边
Prim算法
假设G=(V,E)是一个具有n个顶点的连通网, T=(U,TE)是G的最小生成树,U,TE初值均为空集。
首先从V中任取一个顶点(假定取v1),将它并入U中,此时U={v1},然后只要U是V的真子集(U∈V), 就从那些一个端点已在T中,另一个端点仍在T外 的所有边中,找一条最短边,设为(vi ,vj ),其中 vi∈U,vj∈V-U,并把该边(vi , vj )和顶点vj分别并入T 的边集TE和顶点集U,如此进行下去,每次往生成树里并入一个顶点和一条边,直到n-1次后得到最小生成树。
关键问题:每次如何从连接T中和T外顶点的所有边中,找 到一条最短的
1) 如果用邻接矩阵存放图,而且选取最短边的时候遍历所有点进行选取,则总时间复杂度为 O(V2 ), V为顶点个数
2)用邻接表存放图,并使用堆来选取最短边,则总时间复杂度为O(ElogV)
不加堆优化的Prim 算法适用于密集图,加堆优化的适用于稀疏图
Kruskal算法
假设G=(V,E)是一个具有n个顶点的连通网, T=(U,TE)是G的最小生成树,U=V,TE初值为 空。
将图G中的边按权值从小到大依次选取,若选取的边使生成树不形成回路,则把它并入TE中,若形成回路则将其舍弃,直到TE 中包含N-1条边为止,此时T为最小生成树。
关键问题:如何判断欲加入的一条边是否与生成树 中边构成回路。
利用并查集!
Kruskal 和 Prim 比较
Kruskal:将所有边从小到大加入,在此过程中 判断是否构成回路
– 使用数据结构:并查集
– 时间复杂度:O(ElogE)
– 适用于稀疏图
Prim:从任一节点出发,不断扩展
– 使用数据结构:堆
– 时间复杂度:O(ElogV) 或 O(VlogV+E)(斐波那契堆)
– 适用于密集图
– 若不用堆则时间复杂度为O(V2)
例题:1.POJ 1258 Agri-Net
2.POJ 2349 Arctic Network
3. 2011 ACM/ICPC亚洲区预选赛北京赛站
Problem A. Qin Shi Huang’s National Road System
最短路算法
Dijkstra 算法 解决无负权边的带权有向图 或 无向图的单源最短路问题
用邻接表,不优化,时间复杂度O(V2+E)
Dijkstra+堆的时间复杂度 o(ElgV)
用斐波那契堆可以做到O(VlogV+E)
若要输出路径,则设置prev数组记录每个节点的前趋点,在d[i] 更新时更新prev[i]
Dijkstra算法实现:
已经求出到V0点的最短路的点的集合为T
维护Dist数组,Dist[i]表示目前Vi到V0的“距离”
开始Dist[0] = 0, 其他Dist[i] = 无穷大, T为空集
1) 若|T| = N,算法完成,Dist数组就是解。否则取Dist[i]最 小的不在T中的点Vi, 将其加入T,Dist[i]就是Vi到V0的最短 路长度。
2) 更新所有与Vi有边相连且不在T中的点Vj的Dist值: Dist[j] = min(Dist[j],Dist[i]+W(Vi,Vj))
3) 转到1)
例题:1.POJ 3159 Candies
Bellman-Ford算法
解决含负权边的带权有向图的单源最短路径问题
不能处理带负权边的无向图(因可以来回走一条负权边)
限制条件: 要求图中不能包含权值总和为负值回路(负权值回路),如下图所示。 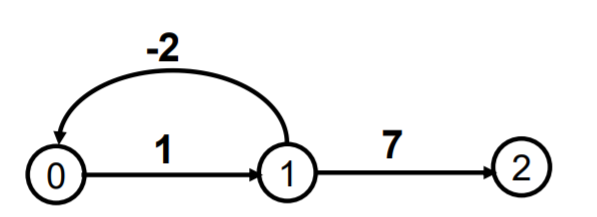
Bellman-Ford算法思想:
构造一个最短路径长度数组序列dist 1 [u], dist 2 [u], …, dist n-1 [u] (u = 0,1…n-1,n为点数)
dist n-1 [u]为从源点v出发最多经过不构成负权值回路的n-1条边到达终点u的 最短路径长度;
算法的最终目的是计算出dist n-1 [u],为源点v到顶点u的最短路径长度。
递推公式(求顶点u到源点v的最短路径):
dist 1 [u] = Edge[v][u]
dist k [u] = min{ dist k-1 [u], min{ dist k-1 [j] + Edge[j][u] } }, j=0,1,…,n-1,j≠u
若存在dist n [u] < dist n-1 [u],则说明存在从源点可达的负权值回路
在求出distn-1[ ]之后,再对每条边<u,k>判断一下:加入这条边是否会使得顶点k的最短路径值再缩短,即判断:dist[u]+w(u,k)<dist[k]否成立,如果成立,则说明存在从源点可达的负权值回路。
存在负权回路就一定能导致该式成立的证明:
如果成立,则说明找到了一条经过了n条边的从 s 到k的路径,且 其比任何少于n条边的从s到k的路径都短。
一共n个顶点,路径却经过了n条边,则必有一个顶点m经过了至少 两次。则m是一个回路的起点和终点。走这个回路比不走这个回路 路径更短,只能说明这个回路是负权回路。
Bellman-Ford算法改进:
Bellman-Ford算法不一定要循环n-1次,n为顶点个数,只要在某次循环过程中,考虑每条边后,源点到所有顶点的最短路径 长度都没有变,那么Bellman-Ford算法就可以提前结束了
Dijkstra算法与Bellman-Ford算法的区别
Dijkstra算法和Bellman算法思想有很大的区别:
Dijkstra算法在求解过程中,源点到集合S内各顶点的最短路径一旦求出,则之后不变了,修改的仅仅是源点到S外各顶点的最短路径长度。
Bellman-Ford算法在求解过程中,每次循环都要修改所有顶点的dist[ ],也就是说源点到各顶点最短路径长度一 直要到算法结束才确定下来。
例题:1.POJ 3259 Wormholes

要求判断任意两点都能仅通过正边就互相可达的有向图(图中有 重边)中是否存在负权环 Sample Input 2 3 3 1 1 2 2 1 3 4 2 3 1 3 1 3 3 2 1 1 2 3 2 3 4 3 1 8 Sample Output NO YES 2个test case 每个test case 第一行: N M W (N<=500,M<=2500,W<=200) N个点 M条双向正权边 W条单向负权边 第一个test case 最后一行 3 1 3 是单向负权边,3->1的边权值是-3

1 //by guo wei 2 #include <iostream> 3 #include <vector> 4 using namespace std; 5 int F,N,M,W; 6 const int INF = 1 << 30; 7 struct Edge 8 { 9 int s,e,w; 10 Edge(int ss,int ee,int ww):s(ss),e(ee),w(ww) { } 11 Edge() { } 12 }; 13 vector<Edge> edges; //所有的边 14 int dist[1000]; 15 int Bellman_ford(int v) 16 { 17 for( int i = 1; i <= N; ++i) 18 dist[i] = INF; 19 dist[v] = 0; 20 for( int k = 1; k < N; ++k) //经过不超过k条边 21 { 22 for( int i = 0; i < edges.size(); ++i) 23 { 24 int s = edges[i].s; 25 int e = edges[i].e; 26 if( dist[s] + edges[i].w < dist[e]) 27 dist[e] = dist[s] + edges[i].w; 28 } 29 } 30 for( int i = 0; i < edges.size(); ++ i) 31 { 32 int s = edges[i].s; 33 int e = edges[i].e; 34 if( dist[s] + edges[i].w < dist[e]) 35 return true; 36 } 37 return false; 38 } 39 int main() 40 { 41 cin >> F; 42 while( F--) 43 { 44 edges.clear(); 45 cin >> N >> M >> W; 46 for( int i = 0; i < M; ++ i) 47 { 48 int s,e,t; 49 cin >> s >> e >> t; 50 edges.push_back(Edge(s,e,t)); //双向边等于两条边 51 edges.push_back(Edge(e,s,t)); 52 } 53 for( int i = 0; i < W; ++i) 54 { 55 int s,e,t; 56 cin >> s >> e >> t; 57 edges.push_back(Edge(s,e,-t)); 58 } 59 if( Bellman_ford(1))//从1可达所有点 60 cout << "YES" <<endl; 61 else cout << "NO" <<endl; 62 } 63 }

for( int k = 1; k < N; ++k) { //经过不超过k条边 for( int i = 0;i < edges.size(); ++i) { int s = edges[i].s; int e = edges[i].e; if( dist[s] + edges[i].w < dist[e]) dist[e] = dist[s] + edges[i].w; } } 会导致在一次内层循环中,更新了某个 dist[x]后,以后又用dist[x]去更新dist[y],这样dist[y]就是经过最多不超过k+1条边的情况了 出现这种情况没有关系,因为整个 for( int k = 1; k < N; ++k) 循环的目的是要确保,对任意点u,如果从源s到u的最短路是经过不超过n-1条边的,则这条最短路不会被忽略。至于计算过程中对某些点 v 计算出了从s->v的经过超过N-1条边的最短路的情况,也不影响结果正确性。若是从s->v的经过超过N-1条边的结果比经过最多N-1条边的结果更小,那一定就有负权回路。有负权回路的情况下,再多做任意多次循环,每次都会发现到有些点的最短路变得更短了。
2.POJ 1860
3.POJ 3259
4.POJ 2240
SPFA算法
快速求解含负权边的带权有向图的单源最短路径问题
是Bellman-Ford算法的改进版,利用队列动态更新dist[]
维护一个队列,里面存放所有需要进行迭代的点。初始时队列中只有一个 源点S。用一个布尔数组记录每个点是否处在队列中。
每次迭代,取出队头的点v,依次枚举从v出发的边v->u,若 Dist[v]+len(v->u) 小于Dist[u],则改进Dist[u](可同时将u前驱记为v)。 此时由于S到u的最短距离变小了,有可能u可以改进其它的点,所以若u不在队列中,就将它放入队尾。这样一直迭代下去直到队列变空,也就是S到所有节点的最短距离都确定下来,结束算法。若一个点最短路被改进的次数达到n ,则有负权环(原因同B-F算法。可以用spfa算法判断图有无负权环
在平均情况下,SPFA算法的期望时间复杂度为O(E)。
例题:1.POJ 3259 Wormholes

要求判断任意两点都能仅通过正边就互相可达的有向图(图中有 重边)中是否存在负权环 Sample Input 2 3 3 1 1 2 2 1 3 4 2 3 1 3 1 3 3 2 1 1 2 3 2 3 4 3 1 8 Sample Output NO YES 2个test case 每个test case 第一行: N M W (N<=500,M<=2500,W<=200) N个点 M条双向正权边 W条单向负权边 第一个test case 最后一行 3 1 3 是单向负权边,3->1的边权值是-3

1 ///POJ3259 Wormholes 判断有没有负权环spfa 2 //by guo wei 3 #include <iostream> 4 #include <vector> 5 #include <queue> 6 #include <cstring> 7 using namespace std; 8 int F,N,M,W; 9 const int INF = 1 << 30; 10 struct Edge 11 { 12 int e,w; 13 Edge(int ee,int ww):e(ee),w(ww) { } 14 Edge() { } 15 }; 16 vector<Edge> G[1000]; //整个有向图 17 int updateTimes[1000]; //最短路的改进次数 18 int dist[1000]; //dist[i]是源到i的目前最短路长度 19 int Spfa(int v) 20 { 21 for( int i = 1; i <= N; ++i) 22 dist[i] = INF; 23 dist[v] = 0; 24 queue<int> que; 25 que.push(v); 26 memset(updateTimes,0,sizeof(updateTimes)); 27 while( !que.empty()) 28 { 29 int s = que.front(); 30 que.pop(); 31 for( int i = 0; i < G[s].size(); ++i) 32 { 33 int e = G[s][i].e; 34 if( dist[e] > dist[s] + G[s][i].w ) 35 { 36 dist[e] = dist[s] + G[s][i].w; 37 que.push(e); //没判队列里是否已经有e,可能会慢一些 38 ++updateTimes[e]; 39 if( updateTimes[e] >= N) return true; 40 } 41 } 42 } 43 return false; 44 } 45 int main() 46 { 47 cin >> F; 48 while( F--) 49 { 50 cin >> N >> M >> W; 51 for( int i = 1; i <1000; ++i) 52 G[i].clear(); 53 int s,e,t; 54 for( int i = 0; i < M; ++ i) 55 { 56 cin >> s >> e >> t; 57 G[s].push_back(Edge(e,t)); 58 G[e].push_back(Edge(s,t)); 59 } 60 for( int i = 0; i < W; ++i) 61 { 62 cin >> s >> e >> t; 63 G[s].push_back(Edge(e,-t)); 64 } 65 if( Spfa(1)) 66 cout << "YES" <<endl; 67 else cout << "NO" <<endl; 68 } 69 }
2.POJ 2387
3.POJ 3256
弗洛伊德算法
用于求每一对顶点之间的最短路径。有向图,无向图均可,也可以有负权边。但不适合于有负权回路的题。
复杂度O(n3)
///弗洛伊德算法伪代码(三层循环) for( int i = 1 ; i <= vtxnum; ++i ) for( int j = 1; j <= vtxnum; ++j) { dist[i][j] = cost[i][j]; // cost是边权值, dist是两点间最短距离 if( dist[i][j] < INFINITE) //i到j有边 path[i,j] = [i]+[j]; //path是路径 } for( k = 1; k <= vtxnum; ++k) //每次求中间点标号不超过k的i到j最短路 for( int i = 1; i <= vtxnum; ++i) for(int j = 1; j <= vtxnum ; ++j) if( dist[i][k] + dist[k][j] < dist[i][j]) { dist[i][j] = dist[i][k]+dist[k][j]; path[i,j] = path[i,k]+path[k,j]; }
例题:1.POJ 3660 Cow Contest
2.POJ 1125
