|
算法导论 课程设计
题 目: 贪心法
学院班级: 1613013 学 号: 16130130216 姓 名: 库 妍 主讲教师: 张立勇 日 期: 2019.5.9
|
一、Knapsack Problem
1、实验题目
下面有5个具有值和权重列表的项目,背包最多可以包含100磅。解决了分数背包和0/1背包问题。
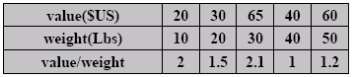
2、使用的算法
部分背包采用动态规划法,0/1背包采用贪心法。
3、算法分析与设计
(1)0/1背包
①描述最优解的结构:考虑重量至多为W磅的最值钱的一包东西。如果我们从中去掉物品j,余下的必须是从除了j以外的n-1件物品中,可以带走的重量至多为W-wj的最值钱的一包东西。
②递归定义最优解的值 :wi表示第i件物体的重量,vi表示第i件物品的价值。定义二维数组c[i, j],其中每个元素代表一个状态,即前i个物体中若干个放入体积为背包中最大价值。c[i-1,j]代表的就是不将这件物品放入背包,而c[i-1,j-vi] + wi则是代表将第i件放入背包之后的总价值。
0/1背包问题的递归式为:
③按自底向上的方式计算最优解的值。
④由计算出的结果构造一个最优解。
(2)部分背包
①决定问题的最优子结构:考虑我们如果从最优的货物中去掉某物品j的重量w,则余下的货物必须是可以从n-1件原有物品和物品j的wj-w磅中可以带走的、重量至多为W-w的一包东西。
②贪心策略:先对每件物品计算其每磅的价值vi/wi。尽量拿每磅价值大的物品。
4、项目测试(功能与性能)
分数背包问题采用选择单位重量价值最大的物品顺序进行挑选,其算法的时间复杂度为O(nlgn)。0/1背包问题的动态规划解法,时间复杂度是O(n)。
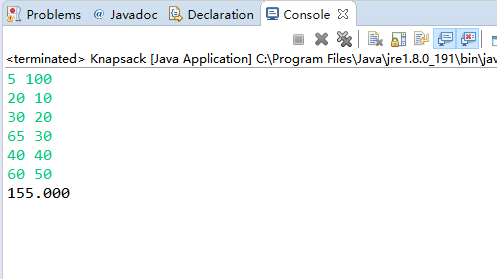
5、实验总结
分数背包问题所采用的贪心策略之不能得到最优解,是由于物品不允许分割,因此,无法保证最终能将背包装满,部分闲置的背包容量使背包的单位重量价值降低了。
一、scheduling problem
1、实验题目
一个简单的调度问题,给予工作编号为J1,J2...Jn,已知所以工作的运行时间分别为T1,T2...TN。有一个单独的处理器,为了安排这些工作以到达减少平均完成时间的最好方法是什么。假定它是一个非抢占式调度:一旦工作开始,它必须运行完成。
a)(j1, j2, j3, j4) : (15,8,3,10)
2、使用的算法
贪心策略
3、算法分析与设计
由于是非抢占式调度,所以应该尽量让时间短的工作先做,然后再让时间长的工作做。这里我们使用堆进行排序,建立一个小顶堆,然后每次拿出小顶堆上的最小元素,并使用sum中的公式就可以算出平均完成时间。堆排序的时间复杂度是O(nlgn),其BuildMinHeap的时间复杂度是O(n),而MinHeap()的时间复杂度是O(lgn)。其中HeapExtractMin()的时间复杂度是O(lgn)。
4、项目测试(功能与性能)
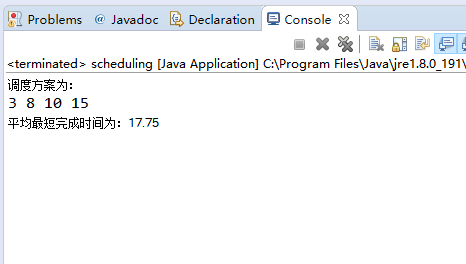
5、实验总结
应用排序算法,让运行时间最短的工作先做。
三、Single-source shortest paths
1、实验题目
以A为源点,求出下图的单源点最短路径。
A B C D E
A -1 3
B 3 2 2
C
D 1 5
E -3
2、使用的算法
由于图中存在负权值,所以Dijkstra算法无法使用,因此采用Bellman-Ford算法求取图的单源点最短路径。
3、算法分析与设计
(1)Bellman-Ford算法通过对边进行松弛操作来渐近地降低从源点A到每个结点的最短路径的估计值,直到该估计值与实际的最短路径权重ơ(A,v)相同为止。该算法返回TRUE值当且仅当输入图中不包含可以从源结点到达的权重为负值的环路。
(2)Bellman-Ford算法的执行步骤:
①初始化:将除源点外的所有顶点的最短距离估计值d[v]←+∞, d[s]←0;
②迭代求解:反复对边集E中的每条边进行松弛操作,使得顶点集V中的每个顶点v的最短距离估计值逐步逼近其最短距离;运行(|v|-1次)
③检验负权回路:判断边集E中的每一条边的两个端点是否收敛。如果存在未收敛的顶点,则算法返回false表明问题无解;否则算法返回true,并且从源点可达的顶点v的最短距离保存在d[v]中。

(3)算法适用范围和条件:
①单源最短路径(从源点A到其它所有顶点v);
②有向图&无向图(无向图可以看作(u,v),(v,u)同属于边集E的有向图);
③边权可正可负(如有负权回路输出错误提示)。
4、项目测试(功能与性能)
Bellman-Ford算法的时间复杂度为θ(VE)。

5、实验总结
Bellman-Ford算法能在一般的情况下(存在负权边的情况下),解决单源最短路径问题。对于给定的有向图G=(V, E),其源点为s,加权函数为w:E→R,对该图运行Bellman-Ford算法返回一个布尔值,表示图中是否存在着一个从源点可达的权为负的回路。若存在回路的话,算法说明该问题无解;若不存在这样的回路,算法将产生最短路径及其权值。
四、All-pairs shortest paths
1、实验题目
求题3图中每对结点的最短路径问题。
2、使用的算法
Floyd-Warshall算法。
3、算法分析与设计
(1)最短路径的结构:设G的顶点为V={1,2,3...n},对于任意一对顶点i,j属于V,假设i到j有路径且中间节点皆属于集合{1,2,3...k},P是其中的一条最小权值路径。就是i到j的最短路径P所通过的中间顶点最大不超过k。
(2)解决每对顶点间最短路径问题的一个递归解:设d(k)ij为从结点i到结点j的所有中间结点全部取自结合{1,2,...,k}的一条最短路径的权重。d(k)ij的递归定义为:
(3)自底向上,计算最短路径的权值:

(4)构造一条最短路径
4、项目测试(功能与性能)
Floyd-Warshall算法的时间复杂度为θ(v^3)。
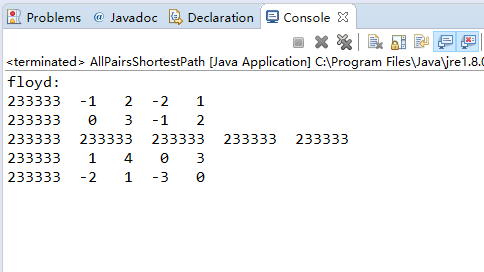
5、实验总结
Floyd-Warshall算法的运行时间是由第3~6行的三重嵌套for循环所决定的。每次执行花费O(1)时间,因此算法的运行时间为Θ(n^3),其代码是紧凑的,而且不包含其他数据结构,因此隐含于Θ记号中的常数是很小的。因此,即便对于中等规模的输入图来说,Floyd-Warshall算法仍然是相当实用的。