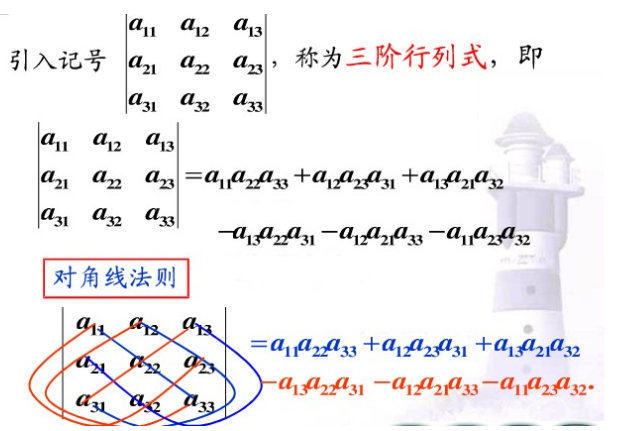
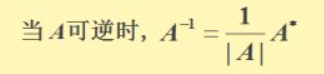因为坐标系转换实现需要求系数矩阵,所以这里只介绍n*n维矩阵求逆矩阵的方法
单位矩阵E定义:
1 0 0 ... 0
0 1 0 ... 0
0 0 1 ... 0
0 0 0 ... 1
对角线上都是1,其他位置全是0
矩阵相乘:
n*n维矩阵A和B相乘(我们用Aij表示A矩阵第i行第j列的值)
(A*B)ij = Ai1*B1j+Ai2*B2j+Ai3*B3j+...+Ain*Bnj
逆矩阵定义:
假设一个n*n维矩阵A,如果存在一个n*n维矩阵B,使得A*B=E,那么就说B是A的逆矩阵A-1,同样A也是B的逆矩阵B-1
一个矩阵的逆矩阵不是一定存在的(可以通过判断行列式的值(也就是矩阵的模)等不等于0来判断逆矩阵存不存在,等于0就不存在逆矩阵)
矩阵行列式求值方法:
我们需要了解等一下矩阵的初等变换:
(1) 交换矩阵的两行(对调i,j,两行记为ri,rj);(2) 以一个非零数k乘矩阵的某一行所有元素(第i行乘以k记为ri×k);(3) 把矩阵的某一行所有元素乘以一个数k后加到另一行对应的元素(第j行乘以k加到第i行记为ri+krj)。类似地,把以上的“行”改为“列”便得到矩阵初等列变换的定义,把对应的记号“r”换为“c”。矩阵的初等行变换与初等列变换合称为矩阵的初等变换。
我们需要知道使用初等变换对矩阵的模的值的改变
第一类初等变换(换行换列)使行列式变号。
第二类初等变换(某行或某列乘k倍)使行列式变k倍。
第三类初等变换(某行(列)乘k倍加到另一行(列))使行列式不变。
上三角矩阵定义:
主对角线以下都是零的方阵称为上三角矩阵。上三角矩阵具有行列式为对角线元素相乘、上三角矩阵乘以系数后也是上三角矩阵、上三角矩阵间的加减法和乘法运算的结果仍是上三角矩阵等性质。
示例:
1 5 6 20 4 8 50 0 3 10 0 0 5为一个上三角矩阵。
计算行列式或者矩阵的时候,可以行变换和列变换混着用吗?
1、计算行列式时,可以同时施加第一、第三类初等行/列变换,施加第二类变换时需要将行列式乘上相应的系数
2、求矩阵的秩时,也即求相抵标准形时,可以施加三种初等行变换,或施加三种初等列变换(不可混用)
3、和单位矩阵拼在一起求逆矩阵时,竖着拼就只能用列变换,横着拼就只能用行变换
4、解方程只能行变换
A矩阵的伴随矩阵A*的求法:
假设A为n阶矩阵,定义矩阵
为A的伴随矩阵,记作
。
,Mij是矩阵A去掉i行j列后,所得矩阵的行列式。
求矩阵逆矩阵的两种方法:
一、根据定义
A-1 = (1/|A|)*A*
求出来A矩阵的模和伴随矩阵就可以
二、构造分块矩阵(A|E)
把分块矩阵(A|E)的A使用初等变换化成E,那么右边的E在跟着A一起初等变换之后的矩阵就是A-1
原理(下图来源于:https://wenku.baidu.com/view/62c266db094e767f5acfa1c7aa00b52acec79c0c.html):


C++代码实现:
代码来源于:https://blog.csdn.net/XX_123_1_RJ/article/details/39268041?locationNum=5&fps=1
代码思想:
采用第二种方法计算逆矩阵
获取行列式的值:把矩阵化为上三角矩阵之后按照定义求矩阵的模(注意,因为代码中fun函数,把矩阵变成上三角矩阵使用了初等行变换的1,3规则,又因为第一条规则会影响到行列式值的正负,所以需要记录一下行交换了几次)
#include<iostream>
#include<iomanip>
using namespace std;
int const n=3; //确定矩阵的节数
/*
作者 星星笔记
*/
int main()
{
void temp(double aa[],double bb[],int n);
double fun(double array[n][n]);
double a[n][n],b[n][2*n],c[n][n],det1,yinzhi;
double bb;
int i,j,kk=0,k,u;
for(i=0;i<n;i++) //初始化一个辅助矩阵
for(j=0;j<2*n;j++)
b[i][j]=0;
//---------输入原始矩阵---------------
cout<<"请输入一个"<<n<<"节方阵"<<endl;
for(i=0;i<n;i++)
for(j=0;j<n;j++)
cin>>a[i][j];
//把矩阵a复制给矩阵b
for(i=0;i<n;i++)
for(j=0;j<n;j++)
b[i][j]=a[i][j];
for(j=0;j<n;j++)
b[j][n+j]=1;
//------------------------------------
//------------测试查看----------
/* cout<<"a所对应的at矩阵b为:"<<endl;
for(i=0;i<n;i++)
for(j=0;j<2*n;j++)
{
cout<<setw(6)<<b[i][j];
kk=kk+1;
if(kk%(2*n)==0)
cout<<endl;
} */
//----------------------------------
// det1=fun(a);//获取行列式的值
for(i=0;i<n;i++)
{
// b[i][i] 等于 0 的情况
if(b[i][i]==0)
for(j=i;j<n;j++)
{
if(b[j][i]!=0)
temp(b[i],b[j],2*n); //交换两行
}
// b[i][i] 不等于 0 的情况
for(k=i+1;k<n;k++)
{
yinzhi = -1 * b[k][i] / b[i][i];
for(u=0; u < 2*n; u++)
{
b[k][u] = b[k][u] + b[i][u] * yinzhi;
}
}
}
det1 = fun(a);// 获取行列式的值,把矩阵化为上三角矩阵之后按照定义求矩阵的模(注意,因为代码中把矩阵变成上三角矩阵使用了初等行变换的1,3规则,又因为第一条规则会影响到行列式值的正负,所以需要记录一下行交换了几次)
if(det1 == 0) // 如果行列式的值为0 则是不可逆的。
{
cout<<"此矩阵不可逆:"<<endl;
return 0;
}
if(det1 != 0)
{
for(i=0; i<n; i++) //左矩阵 的对角线 全部 转化为 1
{
bb = b[i][i]; // bb 不会等于0 因为对角线有有一个为0 说明行列式的值为零,
for(j=0; j<2*n; j++)
b[i][j] = b[i][j] / bb;
}
for(i=n-1; i>0; i--)
for(k=0; k<i; k++)
{
bb = b[k][i];
for(u=0; u<2*n; u++)
b[k][u] = b[k][u] - bb*b[i][u];
}
}
//------------测试查看----------
/* cout<<"变化后的at矩阵"<<endl;
for(i=0;i<n;i++)
for(j=0;j<2*n;j++)
{
cout<<setw(6)<<b[i][j];
kk=kk+1;
if(kk%(2*n)==0)
cout<<endl;
}
cout<<endl; */
//------------------------------
for(i=0; i<n; i++)
for(j=0; j<n; j++)
c[i][j] = b[i][j+n];
kk = 0;
if(det1!=0) //输出逆矩阵
{
cout<<"其可逆且其行列式的值det为:"<<det1<<endl<<endl;
cout<<"可逆a矩阵的逆矩阵为c矩阵:"<<endl;
for(i=0; i<n; i++)
for(j=0; j<n; j++)
{
cout<<setw(15)<<c[i][j];
kk = kk+1;
if(kk%n == 0)
cout<<endl;
}
}
return 0;
}
void temp(double aa[],double bb[],int n)
{ //交换数组指定的两行,即进行行变换(具体为行交换)
int i;
double temp1;
for(i=0; i<n; i++)
{
temp1 = aa[i];
aa[i] = bb[i];
bb[i] = temp1;
}
}
double fun(double array[n][n])
{
int ii,jj,k,u;
int iter = 0;
double det1=1,yin;
for(ii=0; ii<n; ii++)
{
if(array[ii][ii] == 0)
for(jj=ii;jj<n;jj++)
{
if(array[jj][ii] != 0)
{
temp(array[ii],array[jj],n);//交换两行
iter++;
}
}
for(k=ii+1; k<n; k++)
{
yin = -1 * array[k][ii] / array[ii][ii];
for(u=0; u<n; u++)
{
array[k][u] = array[k][u] + array[ii][u] * yin;
}
}
}
for(ii=0;ii<n;ii++)
det1 = det1 * array[ii][ii];
if(iter % 2 == 1)
det1 = -det1;
return (det1); //返回行列式的值
}