区间dp简介

基本思想

即在区间上的动态规划，通过得到子区间的最优解来求得原问题的最优解。

模板

求解在一个区间上的最优解，那么把这个区间分割成一个个小区间，求解每个小区间的最优解，再合并小区间得到大区间即可。枚举区间长度d为每次分割成的小区间长度（由短到长不断合并），内层枚举该长度下可以的起点，自然终点也就明了了。然后在这个起点终点之间枚举分割点，求解这段小区间在某个分割点下的最优解。

for(int d = 1; d <= n; d++){ // 枚举长度
        for(int i = 1; i+d <= n+1; i++){ // 枚举起点，j<=n
            int j = i + d - 1;
            for(int k = i+1; k < j; k++){//枚举分割点，更新小区间最优解
                dp[i][j] = min(dp[i][j], dp[i][k]+dp[k+1][j]+something);
            }
        }
    }

例题

1.矩阵连乘问题
给你2个矩阵A、B，我们使用标准的矩阵相乘定义C=AB如下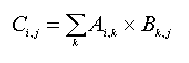： A数组中栏（column）的数目一定要等于B数组中列（row）的数目才可以做此2数组的相乘。若我们以rows(A)，columns(A)分别代表A数组中列及栏的数目，要计算C数组共需要的乘法的数目为：rows(A)columns(B)columns(A)。例如：A数组是一个 10x20的矩阵，B数组是个20x15的矩阵，那么要算出C数组需要做101520，也就是3000次乘法。要计算超过2个以上的矩阵相乘就得决定要用怎样的顺序来做。例如：X、Y、Z都是矩阵，要计算XYZ的话可以有2种选择：(XY)Z 或者 X(YZ)。假设X是5x10的数组，Y是10x20的数组，Z是20x35的数组，那个不同的运算顺序所需的乘法数会有不同： (XY)Z • 52010 = 1000次乘法完成(XY)，并得到一5x20的数组。 • 53520 = 3500次乘法得到最后的结果。 • 总共需要的乘法的次数：1000+3500=4500。 X(YZ) • 103520 = 7000次乘法完成(YZ)，并得到一10x35的数组。 • 53510 = 1750次乘法得到最后的结果。 • 总共需要的乘法的次数：7000+1750=8750。很明显的，我们可以知道计算(XY)Z会使用较少次的乘法。这个问题是：给你一些矩阵，你要写一个程序来决定该如何相乘的顺序，使得用到乘法的次数会最少。
Sample Input

3
1 5
5 20
20 1
3
5 10
10 20
20 35
6
30 35
35 15
15 5
5 10
10 20
20 25
0

Sample Output

Case 1: (A1 x (A2 x A3))
Case 2: ((A1 x A2) x A3)
Case 3: ((A1 x (A2 x A3)) x ((A4 x A5) x A6))

解题思路

规定dp[i][j]为从第i个矩阵乘到第j个矩阵的最优解。

易知当 i == j 时dp[i][j]=0
当 i!=j 时，当在k点断开时，dp[i][j] = dp[i][k] + dp[k+1][j] + p[i-1]*p[k]*p[j],根据题目输入，p[i-1]表示前面得到的矩阵的行数，p[k]后面得到的矩阵的行数，p[j]表示后面得到的矩阵的列数
枚举k的位置即可求得最小的结果

代码(O(n^3))

#include <bits/stdc++.h>

#define ll long long

using namespace std;

int n, cnt = 1;
int p[100], dp[100][100], path[100][100]; // path[i][j]表示第i个矩阵到第j个矩阵的分割点

void PrintPath(int i, int j) { // 递归输出结果
    if(i == j) {
        printf("A%d", i);
        return;
    }
    printf("(");
    PrintPath(i, path[i][j]);
    printf(" x ");
    PrintPath(path[i][j]+1, j);
    printf(")");
}

int MatrixChain() {
    memset(dp, 0, sizeof dp);
    memset(path, 0, sizeof path);
    for (int d = 1; d <= n-1; ++d) { // 枚举区间长度
        for (int i = 1; i <= n-d; ++i) { // 枚举起点，且控制j<=n
            int j = i+d; // 终点
            dp[i][j] = dp[i][i] + dp[i+1][j] + p[i-1]*p[i]*p[j]; // 先从i点开始分割
            path[i][j] = i;
            for (int k = i+1; k < j; ++k) {
                int t = dp[i][k] + dp[k+1][j] + p[i-1]*p[k]*p[j];
                if(t < dp[i][j]) { // 如果t < dp[i][j]更新结果
                    dp[i][j] = t;
                    path[i][j] = k;
                }
            }
        }
    }

    printf("Case %d: ", cnt);
    PrintPath(1, n);
    printf("
");
    cnt++;
    // cout << dp[1][n];
}

int main() {
    int a, b;
    while(scanf("%d", &n)) {
        if(!n) break;
        for (int i = 0; i < n; ++i) {
            scanf("%d%d", &a, &b); // 存储每个矩阵的行数和最后一个矩阵的列数即可
            if(i == n-1) p[i] = a, p[i+1] = b;
            else p[i] = a;
        }
        MatrixChain();
    }
    return 0;
}

参考博文:https://blog.csdn.net/qq_40772692/article/details/80183248