library(readxl) library(TSA) library(fUnitRoots) library(fBasics) library(tseries) library(forecast) library(urca) # 导入数据 xlsx_1<-read_excel("~/Desktop/graduation design/WIND/export for USA.xlsx", sheet = "Sheet2") # 提取数据,300个数据 mon <- xlsx_1[,2] # 构建时间序列 mon.timeseries <- ts(mon,start = c(1995,1),end = c(2019,12),frequency = 12) difflogmon = diff(log(mon.timeseries))
根据时序图可以看到出口序列具有很强的季节性和增长趋势
为了将其变为平稳数据,并且消除趋势,对出口数据取对数差分,得到收益率(增长率)序列
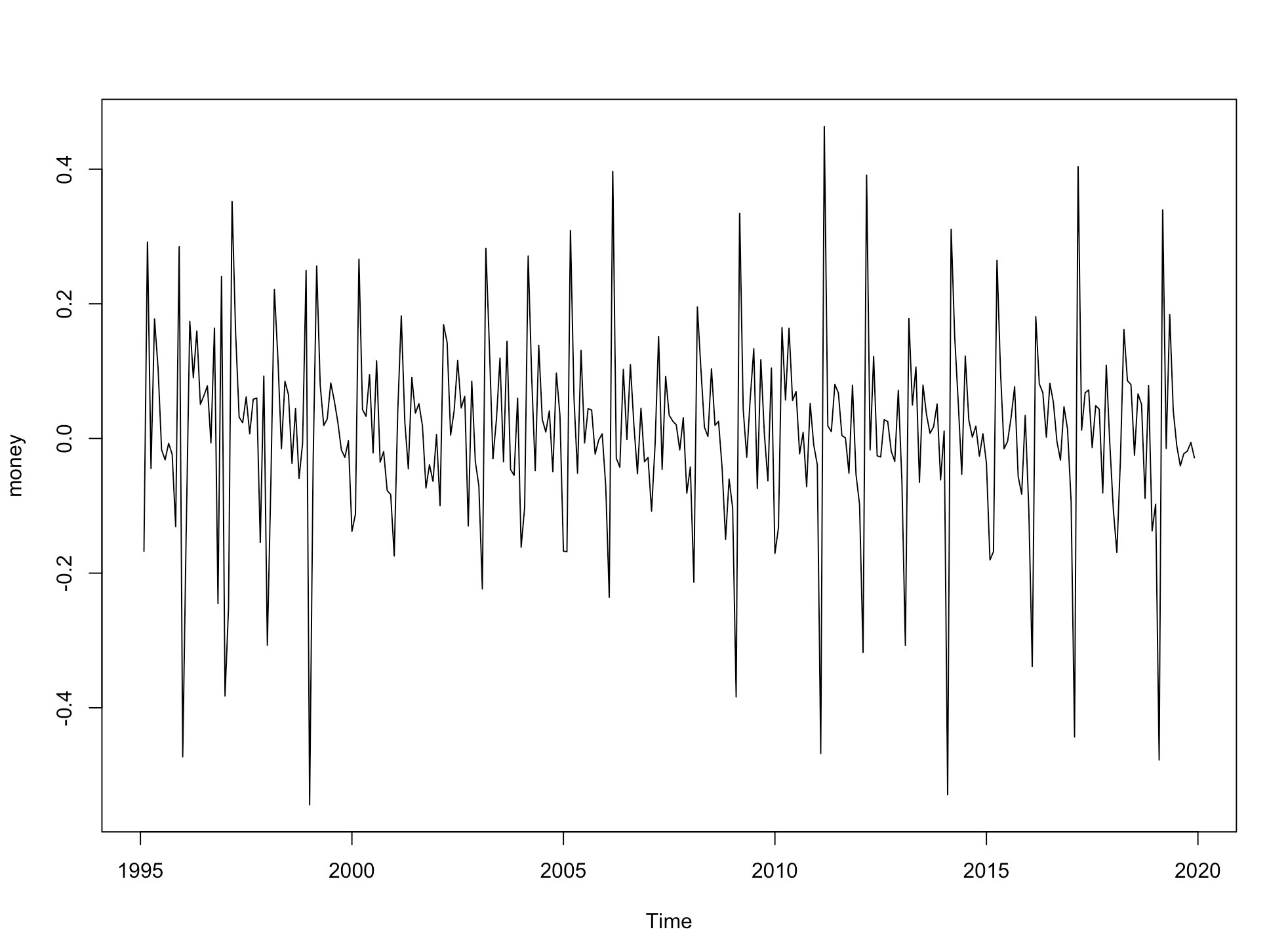
根据上图初步判定收益率为平稳序列
为了能进行变点检验,选取1995-2000的数据建立模型
下面首先进行平稳性检验
mon1.timeseries <- ts(mon,start = c(1995,1),end = c(2000,12),frequency = 12)
difflogmon1 = diff(log(mon1.timeseries))
df = ur.df(difflogmon1) summary(df) ############################################### # Augmented Dickey-Fuller Test Unit Root Test # ############################################### Test regression none Call: lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag) Residuals: Min 1Q Median 3Q Max -0.49342 -0.02738 0.04970 0.10349 0.25371 Coefficients: Estimate Std. Error t value Pr(>|t|) z.lag.1 -1.3776 0.1829 -7.530 1.69e-10 *** z.diff.lag 0.1696 0.1176 1.442 0.154 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.1579 on 67 degrees of freedom Multiple R-squared: 0.6096, Adjusted R-squared: 0.5979 F-statistic: 52.3 on 2 and 67 DF, p-value: 2.072e-14 Value of test-statistic is: -7.53 Critical values for test statistics: 1pct 5pct 10pct tau1 -2.6 -1.95 -1.61
可见收益率序列是平稳的。
作acf与pacf图
acf(as.vector(difflogmon1),lag.max = 36) pacf(as.vector(difflogmon1),lag.max = 36)
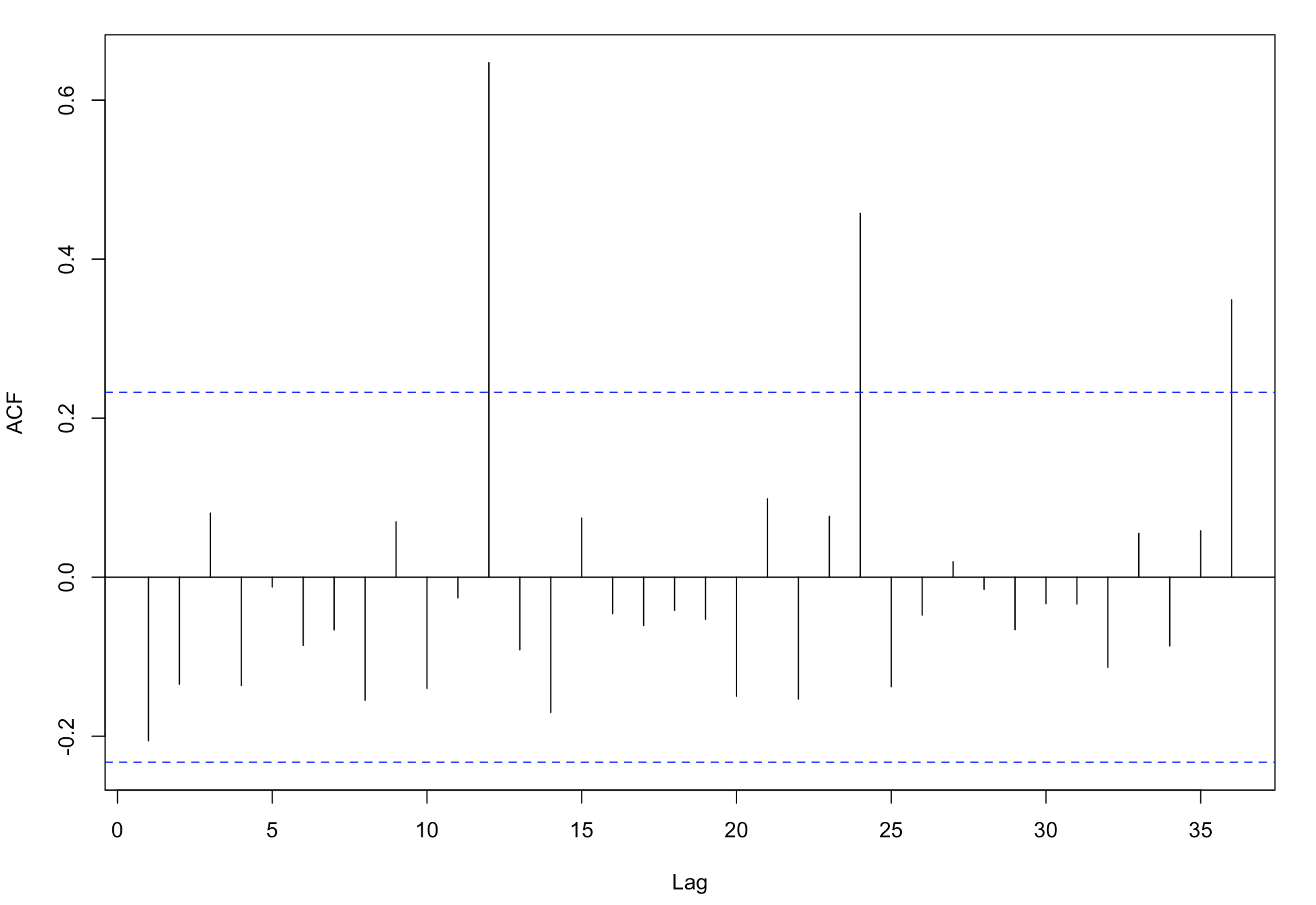
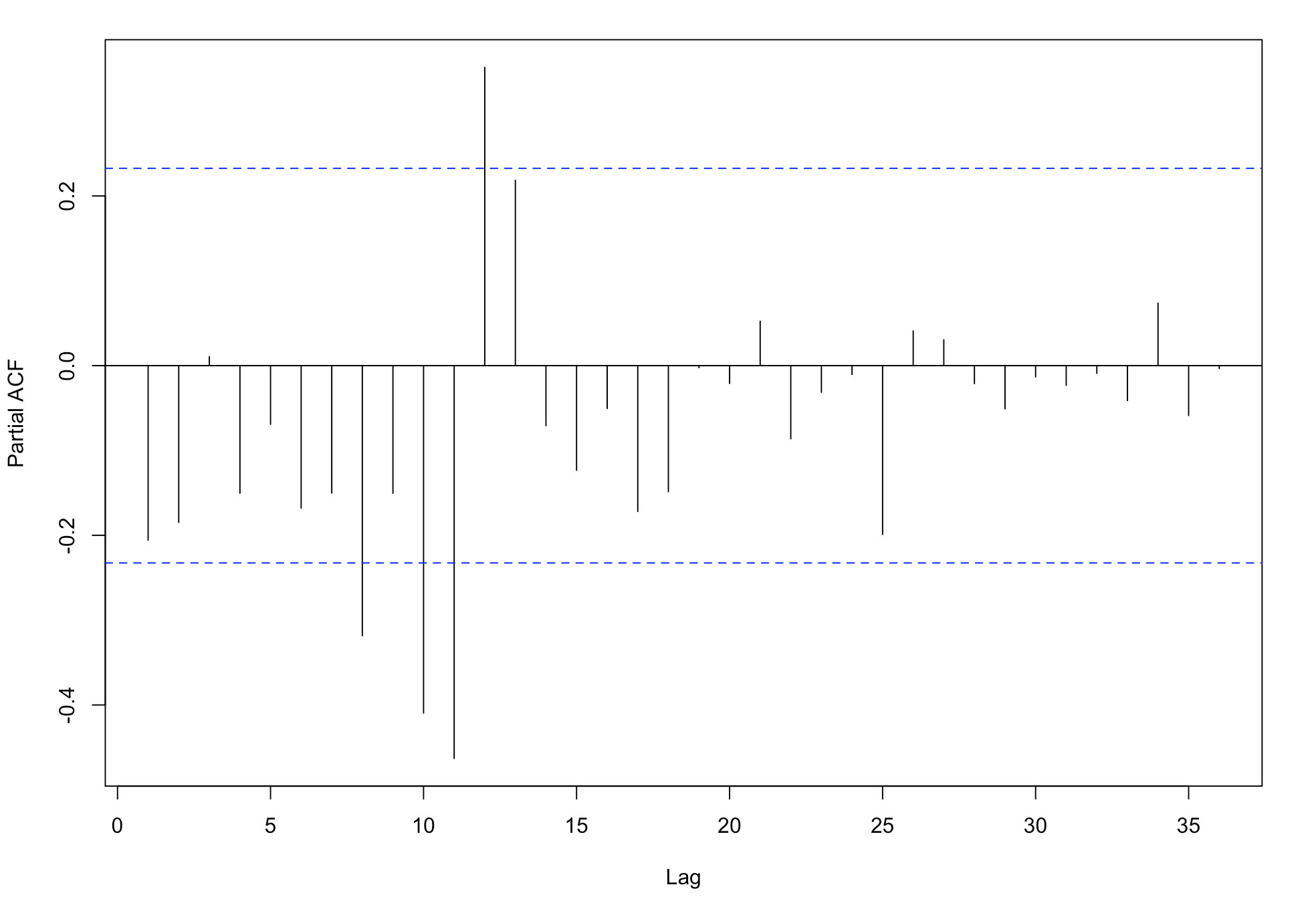
从自相关图来看,数据具有非常强的季节性,并且周期 s = 12。
为了消除季节性,对收益率进行滞后12的一阶差分,观察acf与pacf

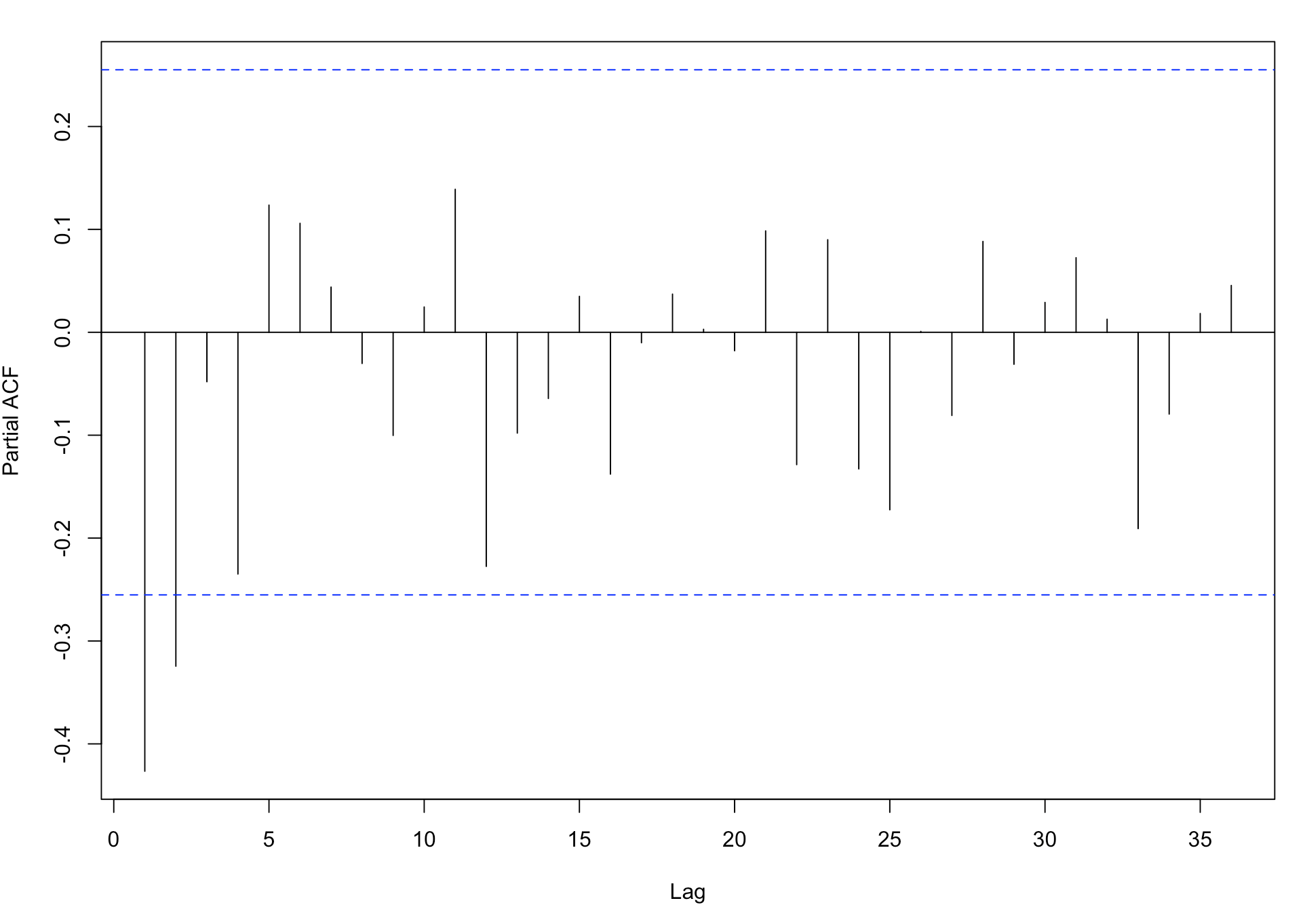
从图中可以看出acf,pacf滞后一阶之后截尾,所以去除季节性的模型应为ARMA(1,1)模型
下面建立季节ARMA模型,消除季节性,利用最大似然法确定参数。
设yt为收益率,根据季节性的特征可能出现在AR或MA中,可能的模型有
![]()
![]()
下面进行参数估计,和利用AIC准则选择最合适的模型
arima(difflogmon1,order = c(1,0,1),seasonal = c(0,1,1)) Call: arima(x = difflogmon1, order = c(1, 0, 1), seasonal = c(0, 1, 1)) Coefficients: ar1 ma1 sma1 -0.0366 -0.5681 -0.4999 s.e. 0.2176 0.1799 0.1602 sigma^2 estimated as 0.006972: log likelihood = 60.83, aic = -115.67 arima(difflogmon1,order = c(1,0,1),seasonal = c(1,1,0)) Call: arima(x = difflogmon1, order = c(1, 0, 1), seasonal = c(1, 1, 0)) Coefficients: ar1 ma1 sar1 -0.0333 -0.5642 -0.3632 s.e. 0.2137 0.1738 0.1345 sigma^2 estimated as 0.007496: log likelihood = 59.58, aic = -113.15
因此选择第二个模型,即建立ARMA(1,0,1)(0,1,1)模型
检验模型
正态性
1.Q-Q图
ar = arima(difflogmon1,order = c(1,0,1),seasonal = c(0,1,1)) qqnorm(ar$residuals) qqline(ar$residuals)
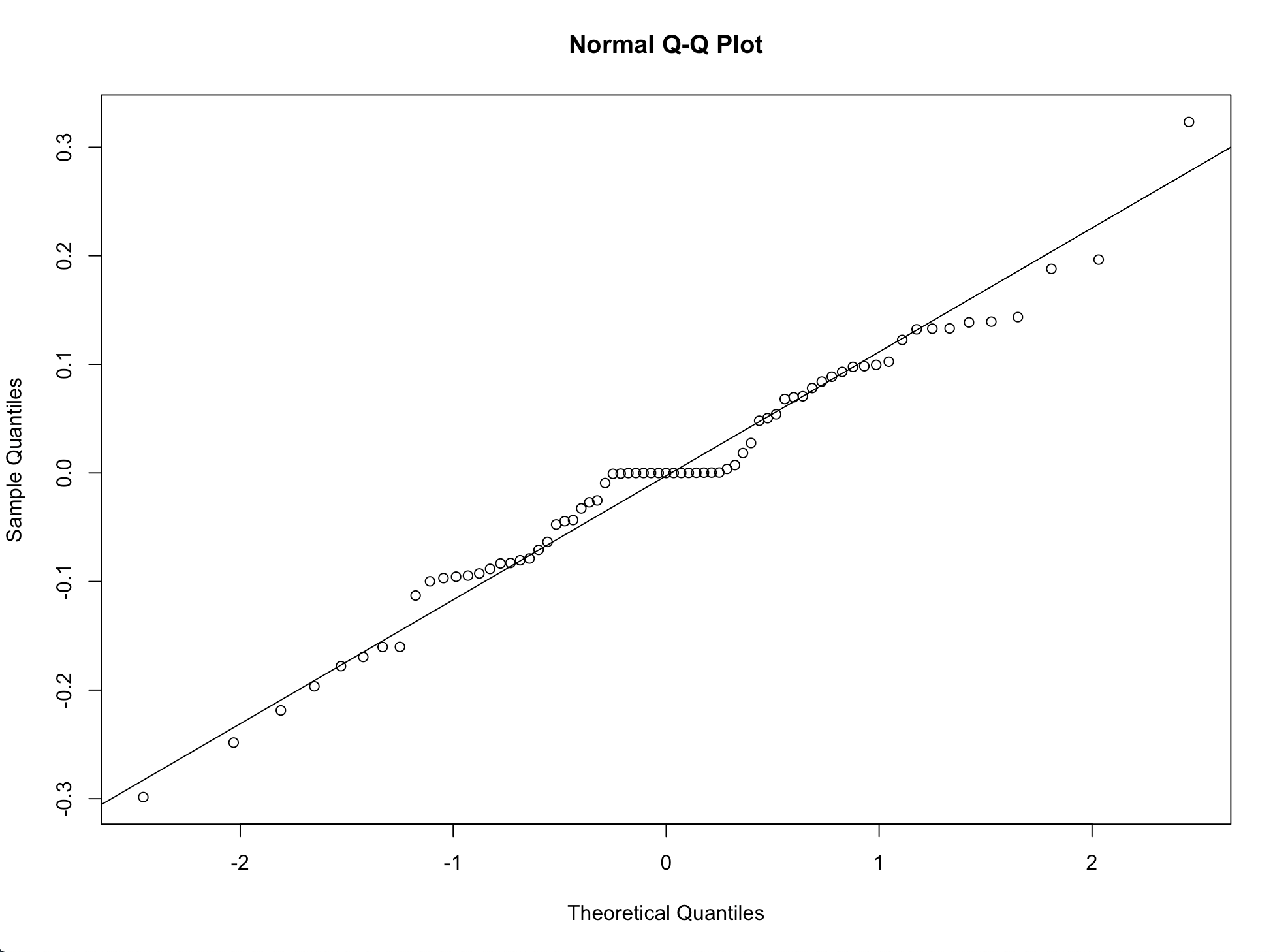
可见模型残差分布在对角线上,符合正态性
2.Shapiro-Wilks检验
shapiro.test(ar$residuals) Shapiro-Wilk normality test data: ar$residuals W = 0.98135, p-value = 0.3725
p值大于0.05,接受正态性检验
独立性
根据Box-Pierce和Ljung-Box的Q统计量检验模型的残差是否为白噪声
ar = arima(difflogmon1,order = c(1,0,1),seasonal = c(0,1,1)) Box.test(ar$residuals) Box-Pierce test data: ar$residuals X-squared = 0.039468, df = 1, p-value = 0.8425
结果接受白噪声的原假设,因此模型建立。
下面的工作是,利用CUSUM构建统计量,检测2001-2019年的变点位置