段段续续的看二分图已经有些时日了。现在借着周末整理一下这么多天对二分图的掌握程度。也好对二分图有个整体的认知。另外,此文只针对与二分图的一些概念和性质,不涉及求最大匹配的算法。好吧,切入正题:
首先我们抛开二分图严谨准确的定义,从一个感性的角度来认识一下什么是二分图。所谓二分图,就是能够把图中的定点分成两个X,Y两部分;并且整个图的边只存在于X与Y之间。就是说,X与Y的内部是不存在边的,否则的话就不是二分图了。举个例子:如果把整个人类中的男人和女人看成顶点,人与人之间的恋爱关系(这里只讨论异性之间的正常恋爱,同性恋是不被承认的)为边来建立图模型的话。那么这其实就是一个二分图,其中的男人为X部分,女人为Y部分。
好了,现在我们给出二分图严谨的科学定义:
假设图G=(V,E)是一个无向图,若顶点集 V 可以分解成两个互不相交的子集(A,B),并且图中的所有边(i,j)的端点 i,j 分别属于子集 A,B 中的元素,则称图 G 是一个二分图。
为了更好的叙述下文,先让我们清楚一个概念:
匹配:无公共点的边集合。(形象点就是 X与Y之间的边的个数)
匹配数:边集中边的个数。
最大匹配:匹配数最大的匹配。
边独立集:指图中边集的一个子集,且该子集中的任意两条边之间没有公共点。(对比匹配的概念我们发现,其实边独立集和匹配是一个概念)
最大边独立集:包含边数最多的边独立集。(其实就是最大匹配,为了方便,以后统称最大匹配)
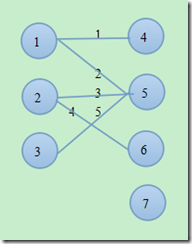
图1
如图1,如果<1,4>是一个合法匹配,那么<1,5>就不是一个合法的匹配,因为它们有公共点1 。同样的如果<2,5>是一个合法的匹配,那么<2,6>和<3,5>就不是一个合法的匹配。不难看出,其中最大匹配是边集:{1, 4, 5},最大匹配数为3 。
独立集:
是指图的顶点集的一个子集,且该子集中的任意两个顶点之间不存在边。如果一个独立集不是任何一个独立集的子集, 那么称这个独立集是一个极大独立集。
最大独立集:一个图中包含顶点数目最多的独立集称为最大独立集。
孤立点:
没有匹配边的点。(需要说明的是,实际上好像没有孤立点官方定义,我在这里用到,是想更直观的突出最大独立集)
根据独立集和匹配以及孤立点的定义,我们可以推断出,独立集就是由孤立点和匹配边的一个端点所组成的(其中,若在每个匹配中选择独立集的端点时,只选择X部或Y部,那么一定不会出错。但是,又有X部又有Y部,可能会出错,也可能不会出错)。那么,我们就得到了一个求最大独立集的一个公式:
最大独立集 = 孤立点 + 最大匹配。(注意,因为孤立点一般不做要求,所以,这个公式是用不到的。事实上,我甚至不确定这个公式的正确性,不过,按定义来讲应该是正确的。下面,我们会给出最大独立集的常用公式)。
如上图1,孤立点:{7}只有一个,最大匹配:{1, 4,5}有三个。所以最大独立集个数 = 1 + 3 = 4 。最大独立集:{1,2,3,7} 或 {4,5,6,7}。
支配集:
是指图顶点集的一个子集,若设L是图G 的一个支配集,则对于图中的任意一个顶点u,要么属于集合L,要么与L中的顶点相邻。 称图G的所有支配集中顶点个数最少的支配集为最小支配集。 通俗点讲,如果我们选中一个点,则称和这个相邻的所有点都被这个点覆盖了。那么支配集,就是找出一些点来覆盖其他的点,最小支配集就是用最小的点来覆盖所有的点。
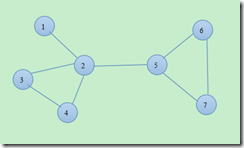
图2
如图2,根据支配集的定义,不难看出{1, 2, 3, 4, 5},{2, 5, 6, 7},{2, 5}都是图2的支配集,其中{2,5}是最小支配集。
最小点覆盖, 最小边覆盖:
是指图的顶点集的一个子集,如果我们选中一个点,则称这个点将所有以它为端点的边都覆盖了。将图中所有的边都覆盖并且用到的顶点数最少的集合就是最小点覆盖。
同样的,我们可以得出边覆盖的定义,边覆盖是指图的边集的一个子集,如果我们选中一条边,则称这条边将它所连的所有端点都覆盖了。将图中所有的点都覆盖并且用到的边数最少的集合就是最小边覆盖。
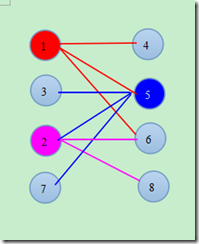
图3
根据,最小点覆盖的定义。我们不难看出,图中三种不同颜色的顶点就是最小点覆盖,仔细观察,我们还知道,此图的最大匹配也刚好是3 。其实,确实有个定理是:
最小点覆盖 = 最大匹配。
最小边覆盖 = 最大独立集 = 顶点总数 - 最大匹配数。
路径覆盖:
路径覆盖就是在图中找一些路经,使之覆盖了图中的所有顶点,且任何一个顶点有且只有一条路径与之关联。其中,路径数目最少的就是最小路径覆盖。
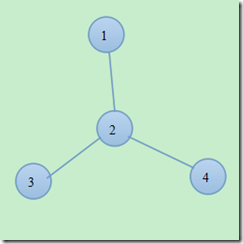
图4
对于路径覆盖,是针对有向图的,走过一条路径之后,不能返回来去走另一条。对于图4,不难看出,最小路径覆盖为 2 。{1,2,3},{4}。当然,你还可以选其他的,不过不管你怎么走,最后都必须至少要2条路径才能覆盖所有的点。
二分图的一些常用概念至此已经记录完了,下面,让我们来看看二分图的一些有用性质:
1. 最小点覆盖 = 最大匹配。
2. 最大独立集 = 顶点总数 - 最大匹配。
证明:
我们先设:总顶点:V。孤立点:X。最大独立集:S。最大匹配:M。现在要证明的是:S=V-M成立。
我们知道,一个匹配对应连个两个端点,且没有公共点。故:V=2*M+X。
根据上面有公式:S = M + X。
那么现在证明 S=V-M就转化为证明M+X=2*M+X - M。显然,这是成立的。故得证。
3. 最小边覆盖 = 顶点总数 - 最大匹配。
4. 最小路径覆盖 = 顶点总数 - 最大匹配。
证明:
我们先假设,最大匹配为0。那么图中不存在边,要想访问所有点,就得有V条路径(V为总顶点数,单个顶点也算是一路径)。如果有一个匹配,那么匹配这条路径就连了两个点,故剩余的V-2个点需V-2条路径覆盖,故为最小路径覆盖=V-1,那么,把匹配数推广到M条。可以得到最小路径覆盖 = V - M。