主成分分析法

因子分析

EM算法求解因子分析

对于EM算法而言，E-步是非常简单的，我们只需要计算Q_i(z⁽ⁱ⁾) =p(z⁽ⁱ⁾|x⁽ⁱ⁾; µ, Λ, Ψ)。然而在这里的条件分布为，z⁽ⁱ⁾|x⁽ⁱ⁾; µ, Λ, Ψ ∼ N (µ_z(i)|x(i) , Σz⁽ⁱ⁾|x⁽ⁱ⁾)，这里满足：

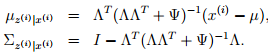
由此，我们得到了E-步的更新公式：

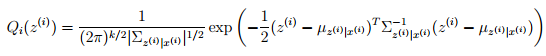
现在，我们想办法解决M-步。我们需要最大化的下式：

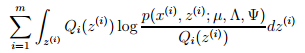
这里的参数是µ, Λ, Ψ。这里仅给出Λ的推导过程。根据我们需要最大化的式子，我们可以化简如下：

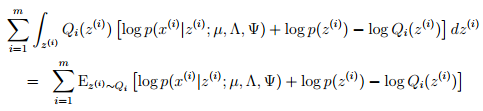
这里的下标z⁽ⁱ⁾∼ Q_i表示z⁽ⁱ⁾服从 Q_i分布。然后去掉与Λ无关的项。得到我们最终想要最大化的结果：

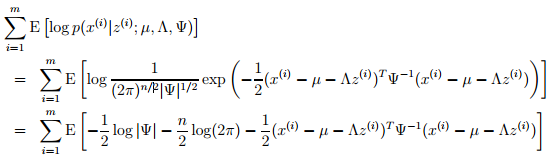
这里，只有最后一项是依赖于Λ的。对其求偏导数，如下：

上述的推导，使用了矩阵的一些公式，对于a ∈ R，tr a = a(tr表示取矩阵的迹)，trAB = trBA，∇AtrABA^TC = CAB + C^TAB。之后，让其等于0，化简结果如下：

因此，我们得到Λ的值如下：

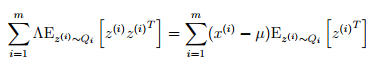
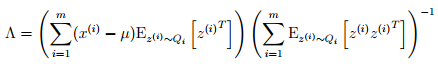
这里我们发现一个有趣的现象。这里得到的Λ结果和回归模型中最小二乘法的方程结果很类似(θ^T= (y^TX )(X^TX )⁻¹)。这里类比一下，x是z的线性函数(包含了一定的噪声)，在E-步中给出了z的估计之后，我们需找的Λ实际上是x和z的线性关系。而最小二乘法也是去寻找特征和结果的直接的线性关系。而这两者很重要的不同点在于最小二乘用的z是最好的猜测(也就是所谓的观测到的分类)。之后，我们会看到这些不同。

为了完成M-步的更新，我们需要求解出Λ结果中的各个期望值。从开始的Q_i定义，我们很容易得到：

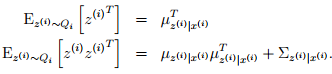
第一步是根据z的条件分布得到的，第二步是根据E[Y Y^T] = E[Y ]E[Y ]^T+ Cov(Y )得到的。再带回到Λ的结果中，得到了M-步中的更新如下：

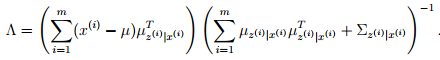
这里很重要的一点是右侧等式中的Σz⁽ⁱ⁾|x⁽ⁱ⁾，这是后验分布p(z⁽ⁱ⁾|x⁽ⁱ⁾)的协方差，M-步中一定要考虑后验分布的z⁽ⁱ⁾不确定性。在使用EM中的一个常见错误是在E-步中，假设我们需要计算潜在变量z的期望E[z]，然后加入到M-步中任何出现z的优化中。这个在简单的问题，比如混合高斯模型中，在因子分析的推导中，我们需要E[zz^T]和E[z]。如我们所见，E[zzT]和E[z]E[z]T需要减去Σz|x。因此，在M-步的更新中考虑后验分布 p(z⁽ⁱ⁾|x⁽ⁱ⁾)的协方差。

最后，给出在M-步中更新参数µ和Ψ的公式。其中，µ在迭代过程中保持不变。

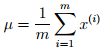
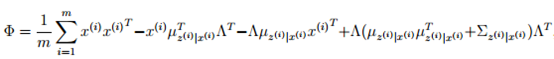
根据上面的EM的过程，要对样本X进行因子分析，只需知道要分解的因子数（z的维度）即可。通过EM，我们能够得到转换矩阵Λ和误差协方差Ψ。因子分析实际上降维，在得到各个参数后，可以求得z，而z的各个参数的含义需要自己去琢磨了。

附录：上面的推导比较理性，这里提供其他的一些说法。因子分析(factor analysis)是一种数据简化的技术。它通过研究众多变量之间的内部依赖关系，探求观测数据中的基本结构，并用少数几个假想变量来表示其基本的数据结构。这几个假想变量能够反映原来众多变量的主要信息。原始的变量是可观测的显在变量，而假想变量是不可观测的潜在变量，称为因子。
1. 主成分分析
在我们讨论因子分析的时候，我们给出了一个模型，即将x ∈ Rⁿ近似的落到k维度子空间，这里的k≪ n。特别的，我们想象得到：每个数据点x(i)都是由k维度下的z⁽ⁱ⁾通过仿射{Λz + µ; z ∈ R^k}变化之后，增加一个均值为0，协方差为Ψ的噪声得到的。因子分析是基于概率模型的，而参数的估计则是使用了EM算法。在这部分，我们将讲述一个模型主成分分析(PCA， Principal Components Analysis)，也是尝试定义一个数据可以映射的子空间。然而，PCA将会采用更直接的方法，但仅要求一些特征向量的计算(在matlab里面，仅仅是命令eig就可以实现)，且不需要使用EM算法。

对于给定的数据集{x⁽ⁱ⁾; i = 1,. . . , m}，包含了汽车的m个不同特征(attribute，表示原始特征或属性)，比如最大速度、转速等等。对于每一个i，x⁽ⁱ⁾ ∈ Rⁿ(n ≪ m)，但是，我们不知道其中有两个特征x_i和x_j都是汽车最大速度，但是前者以"米/小时"为单位，后者以"千米/小时"为单位。因此，这两个特征基本上是线性相关的(因为单位换算的一些四射五入的问题，可能不完全不相同)。因此，这些数据就可以近似的落在n-1维子空间。

我们举另一个例子。考虑一个无线遥控直升飞机(RC 直升飞机，radio-controlled helicopters)飞行员的调查数据，这里的x⁽ⁱ⁾₁衡量了飞行员i的飞行技巧。x⁽ⁱ⁾₂刻画了他是否喜欢飞行。因为RC直升飞机很难操作，只有那些最投入的学生，真正喜欢飞行的学生才能成为好的飞行员。因此x₁和x₂是强相关的。事实上，我们可以通过画图来刻画这种现象，比如飞行员karma，如下图所示，数据基本上都坐落在方向μ₁上，也有一些噪声在该方向上(这里的μ就是我们想要获得的)。

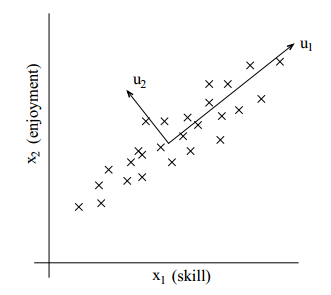
之后我们会具体的看到PCA算法。但是在做PCA之前，通常我们需要先把数据进行标准化(normalize)，即按如下方式标准化：
1. 取μ =
2. 之后，用x⁽ⁱ⁾ – μ 来替换x⁽ⁱ⁾
3. 取σ²_j =
4. 之后，用来替换
这里的第1-2步是减去均值，这样最后的数据的均值就是0，而3-4步则是处以标准差(这里计算中没有使用m-1，通常建议使用m-1)，这样得到的数据最终的方差就是1，即保证了各个特征是在同一个范围内。如果各个数据已经在同一个范围或者范围差距不大的话，那么3-4是可以省略的。

现在，我们已经完成了标准化，那么我们该如何刻画"变量的主要轴" μ(即数据近似落在的方向)呢？一个方法是找到一个单位向量μ，使得当数据投射(projected)到向量μ所在的方向时，投射后数据的方差最大。直观的看，数据开始的时候具有一定量的方差(或信息)，我们希望选择一个方向μ，使得数据落在该方向上后，能够尽可能保持这样的方差(或信息)。（注：在信号处理中认为信号具有较大的方差，噪声有较小的方差，信噪比就是信号与噪声的方差比，越大越好。如前面的图，样本在μ₁的投影方差较大，在μ₂上的投影方差较小，那么认为μ₂上的投影是由噪声引起的。这在最后会有进一步的说明。）

考虑下面一系列数据，这些数据已经经过标准化处理了。

现在考虑我们选择了一个μ，圆点表示原始数据点投射到该向量方向上的点。我们看到：如下图左侧所示，投射后数据具有相当大的方差，且数据点都远离原点。想反，如下图右侧所示，投射后的点具有很小的方差，而且距离原点很近。

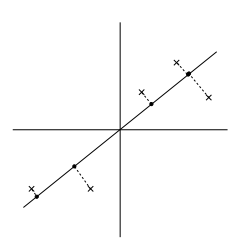
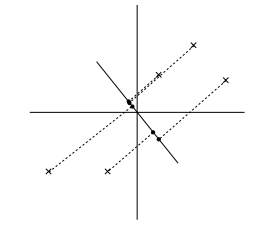
我们希望能够自动选择一个类似于上图左侧的单位向量。为了正式的给出，我们如下表示：对于给定的单位向量μ和一个点x，x投射到向量μ上后的投影长度为x^Tμ。比如，如果x⁽ⁱ⁾是我们数据集中一个点（在二维坐标图上），那么他投射到μ(类似于图上的圆点)。那么投射后点到原点的距离是x^Tμ。故问题转化为最大化投影的方差，因为均值为0，且μ是单位长度的向量，因此我们得到需要最大化的公式如下：

= =

我们可以很容易的看出该最大化受限于||u||²= 1，因此该最大化给出了主特征向量Σ = ，而这恰好是训练集合数据的协方差矩阵（我们假设了数据的均值为0）

总结一下，如果我们希望找到一个一维子空间来近似原始数据，那么我们应该选择的向量是Σ的主特征向量。更普遍的说，如果我们希望把我们的数据投射到k维子空间，我们应该选择的向量u₁, . . . , u_k应该是Σ的前k个特征向量。这里u₁对于数据而言，是正交的。

在这部分，为了表示x⁽ⁱ⁾ ，我们只需要计算相应的矩阵：

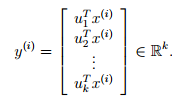
这里x⁽ⁱ⁾∈ Rⁿ，而向量y⁽ⁱ⁾ 现在是一个低纬度的、k维度的，可以近似或替代x⁽ⁱ⁾。PCA因此也可以被称为降维(dimensionality reduction )算法，向量u₁, . . . , u_k，称之为数据的k主成分(principal components )。

注意：尽管上面正式给出的结果是在k=1的情况，而实际上根据特征向量的性质，很容易得到所有的可能正交基(orthogonal bases )u₁, . . . , u_k，用于最大化，因此，我们选择一个正交基来尽可能的保留原始数据的方差。

PCA有很多应用。接下来，我们说一些应用。首先是数据压缩(compression )是一个明显的例子，即用低维度的y⁽ⁱ⁾来表示x⁽ⁱ⁾。如果把高维度数据降到k=2或3，那么我们就可以很容易的可视化y⁽ⁱ⁾，比如如果我们把直升机数据降到2维，那么我们就可以画出来(比如一个轴可能是汽车的类型)去观察各个车可能的聚类结果。

另外一个标准应用是，在监督式学习之前对输入数据x⁽ⁱ⁾进行PCA处理。这不仅仅可以降低计算量，同时降维能够降低假设类(hypothsis class)的复杂度来避免过拟合(比如线性分类器在低维度上的输入空间会有较低的VC维度)。

最后，在我们这个RC直升飞机的例子中，我们也可以认为PCA是一种降低噪音的算法。在我们的例子中，可以看成是从有噪声的飞行员的飞行技术和兴趣度的数据中，估计其内在的飞行能力(即不受噪声干扰的飞行能力)。而课程中，我们也能看到另一个案例，即人脸图片中的特征脸(eigenface )方法。即每张图片x⁽ⁱ⁾∈ R^100×100，是10000维的向量，向量中的每个值表示了人脸图片中100*100的各个像素点。使用PCA，我们可以用更低维度的y⁽ⁱ⁾来表示每张图片x⁽ⁱ⁾，在这样做的过程中，我们希望找到的主成分能够保留捕获不同人脸中一个人是什么样子的主要的变化，但是要去掉因为光线变化、不同的成像条件等造成的噪声。之后我们使用"降维"之后的数据，测试两个脸i，j之间的距离即||y⁽ⁱ⁾− y^{(j )}||²，最后这让人脸匹配和检索算法的结果令人吃惊的好。

注意：关于PCA的解释有9-10多种解释。这里只是给出了最大方差解释，也有最小平方误差解释(把原始数据映射到子空间，衡量子空间好坏的方式不再是方差，而是使得映射后的点到原始点的距离的平方最小)等等。

聚类(k-means)、因子分析、主成分分析，这三种是相互联系的。K-means可以看成是对样本点的划分(这里m > n)，而后两者(m < n)是对变量的划分，而这里如果我们把特征数n和样本数m互换一下，发现这三者是同一性质的。这些都是非监督式学习，可以把非监督式学习看成是含有潜在类别的监督式学习(当然潜在变量是未知的，所以称不上是监督，这里仅是为了对比而已)，这三个方法的主要不同在于：对潜在类别的解释不同。k-means的潜在分类是针对于样本的硬猜测，使得簇内间距很小而簇间间距较大；而因子分析的潜在类别是针对变量的软猜测，潜在变量是服从多元高斯分布；主成分分析的潜在类别则是最优子空间(不同的PCA解释主要区别在于如何定义最优子空间)。