矩阵乘法

矩阵乘法是个很高端的东西。
注意事项： 以下的讲述下标都从0开始

矩阵是什么？

不解释

矩阵加减法？

矩阵加矩阵，就将对应的加上。
矩阵加常数，就将每一个元素都加上这个常数。
减法同理。

矩阵乘法

一张好图，在这里发现的，方便理解矩阵乘法。
矩阵乘法的概念
一个m∗n的的A矩阵，和一个n∗p的B矩阵相乘，将得到一个m∗p的矩阵C

C(i,j)=∑k=1nA(i,k)∗B(k,j)

可以简单地理解为，A中i行的元素，与B中j列的元素，对应相乘得到的和。

矩阵乘法的运算定律

（1） 不满足交换律
（2） 满足结合律：(AB)C=A(BC)
（3） 满足分配律：(A+B)C=AC+BC A(B+C)=AB+AC

模板

template <typename T,int M,int N>
    struct Matrix
    {
        T mat[M][N];
        inline Matrix(){memset(mat,0,sizeof mat);}
        inline T* operator[](int i){return mat[i];}
    };
template <typename T,int M,int N,int P>
    inline Matrix<T,M,P> operator*(const Matrix<T,M,N>& x,const Matrix<T,N,P>& y)
        {
            Matrix<T,M,P> ret;
            int i,j,k;
            for (i=0;i<M;++i)
                for (j=0;j<P;++j)
                    for (k=0;k<N;++k)
                        ret.mat[i][j]+=x.mat[i][k]*y.mat[k][j];
            return ret;
        }
template <typename T,typename T_>
    inline T pow(T x,T_ y)
    {
        T ret=x;
        --y;//这两句话可以忽略初值问题，但y<=0时就悲剧了
        while (y)
        {
            if (y&1)
                ret=ret*x;
            y>>=1;
            x=x*x;  
        }
        return ret;
    }

矩阵乘法的应用

矩阵乘法可以优化时间。
将某些操作转化为矩阵乘法的形式，就可以用快速幂减少时间。因为矩阵乘法满足结合律。

例题一 斐波那契数列

描述

题目背景

大家都知道，斐波那契数列是满足如下性质的一个数列：
• f(1) = 1
• f(2) = 1
• f(n) = f(n-1) + f(n-2) (n ≥ 2 且 n 为整数)

题目描述

请你求出 f(n) mod 1000000007 的值。

输入格式：

·第 1 行：一个整数 n

输出格式：

第 1 行： f(n) mod 1000000007 的值

输入样例#1：

5

输出样例#1：

5

输入样例#2：

10

输出样例#2：

55

说明

对于 60% 的数据： n ≤ 92
对于 100% 的数据： n在long long(INT64)范围内。

解法

这是一道裸斐波拉契数列。传统递推是O(N)的，显然会炸。
斐波拉契数列有个通项，但我们在这里用矩阵乘法解决。
我们知道f(n)是由f(n-1)和f(n-2)推过来的，不妨设一个1*2的矩阵

A=[f(n−2)f(n−1)]

现在我们要通过A推出B
B=[f(n−1)f(n)]=[f(n−1)f(n−2)+f(n−1)]

我们要求出一个2*2的 转移矩阵 T，满足
A∗T=B

即
[f(n−2)f(n−1)]∗T=[f(n−1)f(n−2)+f(n−1)]

我们知道，B[0][0]=A[0][1] B[0][1]=A[0][0]+A[0][1]
对于T[0][0]，A[0][0]对B[0][0]没有贡献，所以T[0][0]=0
对于T[1][0]，A[0][1]对B[0][0]有贡献，B[0][0]=A[0][1]*1，所以T[1][0]=1
对于T[0][1]，A[0][0]对B[0][1]有贡献，B[0][1]=A[0][0]*1+A[0][1]*1，所以T[0][1]=1
对于T[1][1]，A[1][1]对B[0][1]有贡献，B[1][1]=A[0][0]*1+A[0][1]*1，所以T[1][1]=1
综上所述，
T=[0111]

显然这个式子是正确的。
[f(n−2)f(n−1)]∗[0111]=[f(n−1)f(n−2)+f(n−1)]

求出这个矩阵后，就可以愉快地快速幂了。
时间复杂度O(lgN)

代码

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define mod 1000000007
template <typename T,int M,int N>
    struct Matrix
    {
        T mat[M][N];
        inline Matrix(){memset(mat,0,sizeof mat);}
        inline T* operator[](int i){return mat[i];}
    };
template <typename T,int M,int N,int P>
    inline Matrix<T,M,P> operator*(const Matrix<T,M,N>& x,const Matrix<T,N,P>& y)
        {
            Matrix<T,M,P> ret;
            int i,j,k;
            for (i=0;i<M;++i)
                for (j=0;j<P;++j)
                    for (k=0;k<N;++k)
                        (ret.mat[i][j]+=x.mat[i][k]*y.mat[k][j])%=mod;
            return ret;
        }
template <typename T,typename T_>
    inline T pow(T x,T_ y)
    {
        T ret=x;
        --y;
        while (y)
        {
            if (y&1)
                ret=ret*x;
            y>>=1;
            x=x*x;  
        }
        return ret;
    }
int main()
{
    long long n;
    scanf("%lld",&n);
    if (n==1)
        putchar('1');
    else
    {
        Matrix<long long,2,2> tmp;
        tmp[0][1]=tmp[1][0]=tmp[1][1]=1;
        tmp=pow(tmp,n-1);
        Matrix<long long,1,2> a;
        a[0][1]=1;//a=[f(0) f(1)]
        a=a*tmp;//[f(0) f(1)]*(T^(n-1))=[f(n-1) f(n)]
        printf("%lld
",a[0][1]);
    }
}

例题二 【NOIP2013模拟联考14】图形变换

Description

翔翔最近接到一个任务，要把一个图形做大量的变换操作，翔翔实在是操作得手软，决定写个程序来执行变换操作。
翔翔目前接到的任务是，对一个由n个点组成的图形连续作平移、缩放、旋转变换。相关操作定义如下：
Trans(dx,dy) 表示平移图形，即把图形上所有的点的横纵坐标分别加上dx和dy；
Scale(sx,sy) 表示缩放图形，即把图形上所有点的横纵坐标分别乘以sx和sy；
Rotate(θ,x0,y0) 表示旋转图形，即把图形上所有点的坐标绕(x0,y0)顺时针旋转θ角度
由于某些操作会重复运行多次，翔翔还定义了循环指令：
Loop(m)
…
End
表示把Loop和对应End之间的操作循环执行m次，循环可以嵌套。

Input

第一行一个整数n(n<=100)表示图形由n个点组成；
接下来n行，每行空格隔开两个实数xi，yi表示点的坐标；
接下来一直到文件结束，每行一条操作指令。保证指令格式合法，无多余空格。

Output

输出有n行，每行两个空格隔开实数xi，yi表示对应输入的点变换后的坐标。
本题采用Special Judge判断，只要你输出的数值与标准答案误差不能超过1即可。

Sample Input

3
0.5 0
2.5 2
-4.5 1
Trans(1.5,-1)
Loop(2)
Trans(1,1)
Loop(2)
Rotate(90,0,0)
End
Scale(2,3)
End

Sample Output

10.0000 -3.0000
18.0000 15.0000
-10.0000 6.0000

Data Constraint

保证操作中坐标值不会超过double范围，输出不会超过int范围；
指令总共不超过1000行；
对于所有的数据,所有循环指令中m<=1000000；
对于60%的数据,所有循环指令中m<=1000；
对于30%的数据不含嵌套循环。

Hint

【友情提醒】
pi的值最好用系统的值。C++的定义为：#define Pi M_PI
Pascal就是直接为：pi
不要自己定义避免因为pi带来的误差。

解法

旋转公式：

绕(a,b)逆时针转θx′=(x−a)∗cosθ−(y−b)∗sinθ+ay′=(x−a)∗sinθ+(y−b)∗cosθ+b

暴力铁定超时。
先考虑使用2*2的转移矩阵T，但是只能对付乘法，加法和旋转就要用矩阵加法了。矩阵乘法和矩阵加法混在一起很麻烦（矩阵套矩阵？）。
我们可以新增一个常数项
A=[xy1]

现在要求出T1、T2、T3满足
[xy1]∗T1=[x+ay+b1][xy1]∗T2=[x∗ay∗b1][xy1]∗T3=[(x−a)∗cosθ−(y−b)∗sinθ+a(x−a)∗sinθ+(y−b)∗cosθ+b1]

这样加、乘就特别容易，将旋转公式用乘法分配律拆开，也可以得出转移矩阵
T1=⎡⎣⎢10a01b001⎤⎦⎥T2=⎡⎣⎢a000b0001⎤⎦⎥T3=⎡⎣⎢cosθ−sinθa−a∗cosθ+b∗sinθsinθcosθb−a∗sinθ−b∗cosθ001⎤⎦⎥

可以代进去看看，是成立的。
于是我们可以将所有操作乘起来（有循环时递归，算出这个循环里一次的乘积后快速幂），最后在将每个坐标乘这个积，就是答案。

代码

英语不好，将theta打成xida，懒得改，注意一下就好了。

#include <cstdio>
#include <cstring>
#include <cmath>
#include <cassert>
#include <algorithm>
using namespace std;
#define I_O(x) freopen(""#x".in","r",stdin);freopen(""#x".out","w",stdout)
#define Pi 3.14159265358979323846
template <typename T,int M,int N>
    struct Matrix
    {
        T mat[M][N];
        inline Matrix(){memset(mat,0,sizeof mat);}
        inline T* operator[](int i){return mat[i];}
    };
template <typename T,int M,int N,int P>
    inline Matrix<T,M,P> operator*(const Matrix<T,M,N>& x,const Matrix<T,N,P>& y)
        {
            Matrix<T,M,P> ret;
            int i,j,k;
            for (i=0;i<M;++i)
                for (j=0;j<P;++j)
                    for (k=0;k<N;++k)
                        ret.mat[i][j]+=x.mat[i][k]*y.mat[k][j];
            return ret;
        }
template <typename T,typename T_>
    inline T pow(T x,T_ y)
    {
        T ret=x;
        --y;
        while (y)
        {
            if (y&1)
                ret=ret*x;
            y>>=1;
            x=x*x;  
        }
        return ret;
    }
int n;
Matrix<double,1,3> d[100];
char cz[101];
Matrix<double,3,3> dfs(int);
int main()
{
    I_O(transform);
    scanf("%d",&n);
    int i;
    double x,y;
    for (i=0;i<n;++i)
    {
        scanf("%lf%lf",&d[i][0][0],&d[i][0][1]);
        d[i][0][2]=1;
    }
    Matrix<double,3,3> a,tmp1,tmp2,tmp3;//分三个变量是为避免多次赋值
    a[0][0]=a[1][1]=a[2][2]=1;//a的初值
    tmp1[0][0]=tmp1[1][1]=tmp1[2][2]=1;
    tmp2[2][2]=1;
    tmp3[2][2]=1;
    double xida,tmp_sin,tmp_cos;
    int t;
    while (scanf("%s",cz)==1)
    {
        switch (*cz)
        {
            case 'T':
//              1 0 0
//              0 1 0
//              a b 1
                sscanf(cz,"Trans(%lf,%lf",&tmp1[2][0],&tmp1[2][1]);
                a=a*tmp1;
            break;
            case 'S':
//              a 0 0
//              0 b 0
//              0 0 1
                sscanf(cz,"Scale(%lf,%lf",&tmp2[0][0],&tmp2[1][1]);
                a=a*tmp2;
            break;
            case 'R':
                sscanf(cz,"Rotate(%lf,%lf,%lf",&xida,&x,&y);
                xida=-xida/180*Pi;//顺时针角度转成逆时针弧度
//              cos           sin           0
//              -sin          cos           0
//              a-a*cos+b*sin b-a*sin-b*cos 1
                tmp_sin=sin(xida);
                tmp_cos=cos(xida);
                tmp3[0][0]=tmp_cos; tmp3[0][1]=tmp_sin; tmp3[0][2]=0;
                tmp3[1][0]=-tmp_sin; tmp3[1][1]=tmp_cos; tmp3[1][2]=0;
                tmp3[2][0]=x-x*tmp_cos+y*tmp_sin; tmp3[2][1]=y-x*tmp_sin-y*tmp_cos;
                a=a*tmp3;
            break;
            default:
                sscanf(cz,"Loop(%d",&t);
                a=a*dfs(t);
        }
    }
    Matrix<double,1,3> tmp;
    for (i=0;i<n;++i)
    {
        tmp=d[i]*a;
        printf("%.4lf %.4lf
",tmp[0][0],tmp[0][1]);
    }
}
Matrix<double,3,3> dfs(int t)
{
    double x,y;
    Matrix<double,3,3> a,tmp1,tmp2,tmp3;
    a[0][0]=a[1][1]=a[2][2]=1;
    tmp1[0][0]=tmp1[1][1]=tmp1[2][2]=1;
    tmp2[2][2]=1;
    tmp3[2][2]=1;
    int times;
    double xida,tmp_sin,tmp_cos;
    for (scanf("%s",cz);*cz!='E';scanf("%s",cz))
    {
        switch (*cz)
        {
            case 'T':
                sscanf(cz,"Trans(%lf,%lf",&tmp1[2][0],&tmp1[2][1]);
//              1 0 0
//              0 1 0
//              a b 1
                a=a*tmp1;
            break;
            case 'S':
                sscanf(cz,"Scale(%lf,%lf",&tmp2[0][0],&tmp2[1][1]);
//              a 0 0
//              0 b 0
//              0 0 1
                a=a*tmp2;
            break;
            case 'R':
                sscanf(cz,"Rotate(%lf,%lf,%lf",&xida,&x,&y);
                xida=-xida/180*Pi;
//              cos           sin           0
//              -sin          cos           0
//              a-a*cos+b*sin b-a*sin-b*cos 1
                tmp_sin=sin(xida);
                tmp_cos=cos(xida);
                tmp3[0][0]=tmp_cos; tmp3[0][1]=tmp_sin; tmp3[0][2]=0;
                tmp3[1][0]=-tmp_sin; tmp3[1][1]=tmp_cos; tmp3[1][2]=0;
                tmp3[2][0]=x-x*tmp_cos+y*tmp_sin; tmp3[2][1]=y-x*tmp_sin-y*tmp_cos;
                a=a*tmp3;
            break;
            default:
                sscanf(cz,"Loop(%d",&times);
                a=a*dfs(times);
        }
    }
    return pow(a,t);
}

例题三 【SDOI2009】HH去散步

描述

题目描述

HH有个一成不变的习惯，喜欢饭后百步走。所谓百步走，就是散步，就是在一定的时间 内，走过一定的距离。 但是同时HH又是个喜欢变化的人，所以他不会立刻沿着刚刚走来的路走回。 又因为HH是个喜欢变化的人，所以他每天走过的路径都不完全一样，他想知道他究竟有多 少种散步的方法。
现在给你学校的地图（假设每条路的长度都是一样的都是1），问长度为t，从给定地 点A走到给定地点B共有多少条符合条件的路径

输入格式：

第一行：五个整数N，M，t，A，B。其中N表示学校里的路口的个数，M表示学校里的 路的条数，t表示HH想要散步的距离，A表示散步的出发点，而B则表示散步的终点。
接下来M行，每行一组Ai，Bi，表示从路口Ai到路口Bi有一条路。数据保证Ai != Bi，但 不保证任意两个路口之间至多只有一条路相连接。 路口编号从0到N − 1。 同一行内所有数据均由一个空格隔开，行首行尾没有多余空格。没有多余空行。 答案模45989。

输出格式：

一行，表示答案。

输入样例#1：

4 5 3 0 0
0 1
0 2
0 3
2 1
3 2

输出样例#1：

4

说明

对于30%的数据，N ≤ 4，M ≤ 10，t ≤ 10。
对于100%的数据，N ≤ 50，M ≤ 60，t ≤ 2^30，0 ≤ A,B

解法

先说一下大意（我等好久才弄懂）。
给你一张图，要从A走到B，不能走上一次走的路，要走t步，问方案数。
不能走上一次走的路，一次。
举个例子：
例子
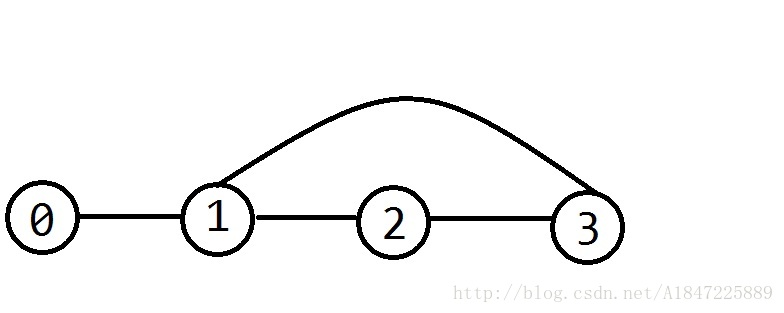
路径可以这样：0->1->2->3->1->0
所以我们可以想到DP
设f[i][j]表示第i步走了j这条边的方案数，这样在转移时，就可以方便地判断，避免走上一次走的路。
转移：f[i][bc]=∑ab≠bcf[i−1][ab]
但是，我们发现，每次的决策点都是一样的，很明显能直接用矩阵乘法来转移，快速幂即可。

代码

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
using namespace std;
template <typename T,int M,int N>
    struct Matrix
    {
        T mat[M][N];
        inline Matrix(){memset(mat,0,sizeof mat);}
        inline T* operator[](int i){return mat[i];}
    };
template <typename T,int M,int N,int P>
    inline Matrix<T,M,P> operator*(const Matrix<T,M,N>& x,const Matrix<T,N,P>& y)
        {
            Matrix<T,M,P> ret;
            int i,j,k;
            for (i=0;i<M;++i)
                for (j=0;j<P;++j)
                    for (k=0;k<N;++k)
                        ret.mat[i][j]+=x.mat[i][k]*y.mat[k][j];
            for (i=0;i<M;++i)
                for (j=0;j<P;++j)
                    ret.mat[i][j]%=45989;//减少mod运算（mod运算很慢的）
            return ret;
        }
template <typename T,typename T_>
    inline T pow(T x,T_ y)
    {
        T ret=x;
        --y;
        while (y)
        {
            if (y&1)
                ret=ret*x;
            y>>=1;
            x=x*x;  
        }
        return ret;
    }
int n,m,t,u,v;
struct EDGE
{
    int from,to;
    EDGE* las;
    EDGE* rev;
} e[120];
EDGE* last[20];
Matrix<long long,1,120> f;
Matrix<long long,120,120> T;
int li[60];//用于记录连接终点的边
int nl;
int main()
{
    scanf("%d%d%d%d%d",&n,&m,&t,&u,&v);
    int i,j=-1,x,y;
    for (i=1;i<=m;++i)
    {
        scanf("%d%d",&x,&y);
        ++j;
        e[j]={x,y,last[x],e+j+1};
        last[x]=e+j;
        if (y==v)
            li[nl++]=j;
        ++j;
        e[j]={y,x,last[y],e+j-1};
        last[y]=e+j;
        if (x==v)
            li[nl++]=j;
    }
    EDGE* ei;
    for (ei=last[u];ei;ei=ei->las)
        f[0][int(ei-e)]=1;
    m<<=1;
    EDGE *ej,*end=e+m;
    for (ei=e;ei<end;++ei)
        for (ej=last[ei->to];ej;ej=ej->las)
            if (ei->rev!=ej)
                T[int(ei-e)][int(ej-e)]=1;//生成转移矩阵
    f=f*pow(T,t-1);
    int ans=0; 
    for (i=0;i<nl;++i)
        ans+=f[0][li[i]];
    printf("%d
",ans%45989);
}

总结

  1. 遇到矩阵乘法的题，先将转移后的式子拆开，再帮它配转移矩阵。
  2. 如果用普通的方式配矩阵必须出现加法，那么可以尝试加常数项上去。
  3. 若有某些DP（还是递推？）的题目的决策点固定，那么可以在程序中生成转移矩阵，直接快速幂。

补充

矩阵乘法模板2.0

template <typename T,int M,int N>
    struct Matrix
    {
        int m,n;
        T mat[M][N];
        inline Matrix(){m=M;n=N;memset(mat,0,sizeof mat);}
        inline void SetUpSize(int _m,int _n){m=_m;n=_n;} 
        inline T* operator[](int i){return mat[i];}
    };
template <typename T,int M,int N,int P>
inline Matrix<T,M,P> operator*(const Matrix<T,M,N>& x,const Matrix<T,N,P>& y)
    {
        Matrix<T,M,P> ret;
        int i,j,k;
        for (i=0;i<x.m;++i)
            for (j=0;j<y.n;++j)
                for (k=0;k<x.n;++k)
                    ret.mat[i][j]+=x.mat[i][k]*y.mat[k][j];
        return ret;
    }
template <typename T,typename T_>
    inline T pow(T x,T_ y)
    {
        T ret=x;
        --y;//这两句话可以忽略初值问题，但y<=0时就悲剧了
        while (y)
        {
            if (y&1)
                ret=ret*x;
            y>>=1;
            x=x*x;  
        }
        return ret;
    }
【推广】 免费学中医，健康全家人
原文地址：https://www.cnblogs.com/jz-597/p/11145307.html