Trie树和后缀树(转，简化)

作者：July、yansha。
出处：http://blog.csdn.net/v_JULY_v 。

　　1.Trie树

　　1)简述

　　又称单词查找树，Trie树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希表高。

　　3个基本性质：

根节点不包含字符，除根节点外每一个节点都只包含一个字符。
从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
每个节点的所有子节点包含的字符都不相同。

　　假设有b，abc，abd，bcd，abcd，efg，hii 这6个单词。

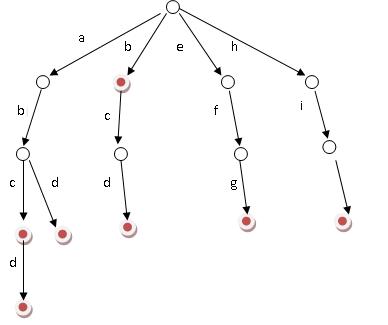
　　好比大海搜人，立马就能确定东南西北中的到底哪个方位，如此迅速缩小查找的范围和提高查找的针对性。

　　那么，对于一个单词，我只要顺着他从根走到对应的节点，再看这个节点是否被标记为红色就可以知道它是否出现过了。把这个节点标记为红色，就相当于插入了这个单词。

　　2)比较

　　已知n个由小写字母构成的平均长度为10的单词,判断其中是否存在某个串为另一个串的前缀子串。下面对比3种方法：

最容易想到的：即从字符串集中从头往后搜，看每个字符串是否为字符串集中某个字符串的前缀，复杂度为O(n^2)。
使用hash：我们用hash存下所有字符串的所有的前缀子串，建立存有子串hash的复杂度为O(n*len)，而查询的复杂度为O(n)* O(1)= O(n)。
使用trie：因为当查询如字符串abc是否为某个字符串的前缀时，显然以b,c,d....等不是以a开头的字符串就不用查找了。所以建立trie的复杂度为O(n*len)，而建立+查询在trie中是可以同时执行的，建立的过程也就可以成为查询的过程，hash就不能实现这个功能。所以总的复杂度为O(n*len)，实际查询的复杂度也只是O(len)。（说白了，就是Trie树的平均高度h为len，所以Trie树的查询复杂度为O（h）=O（len）。好比一棵二叉平衡树的高度为logN，则其查询，插入的平均时间复杂度亦为O（logN））。

下面解释下上述方法3中所说的为什么hash不能将建立与查询同时执行，而Trie树却可以：

在hash中，例如现在要输入两个串911，911456，如果要同时查询这两个串，且查询串的同时若hash中没有则存入。那么，这个查询与建立的过程就是先查询其中一个串911，没有，然后存入9、91、911；而后查询第二个串911456，没有然后存入9、91、911、9114、91145、911456。因为程序没有记忆功能，所以并不知道911在输入数据中出现过，只是照常以例行事，存入9、91、911、9114、911...。也就是说用hash必须先存入所有子串，然后for循环查询。
而trie树中，存入911后，已经记录911为出现的字符串，在存入911456的过程中就能发现而输出答案；倒过来亦可以，先存入911456，在存入911时，当指针指向最后一个1时，程序会发现这个1已经存在，说明911必定是某个字符串的前缀。

　　3)代码实现

  1 // trie tree.cpp : 定义控制台应用程序的入口点。
  2 //
  3 #include "stdafx.h"
  4 //功能：统计一段英文的单词频率(文章以空格分隔，没有标点) 
  5 //思路：trie节点保存单词频率，然后通过DFS按字典序输出词频 
  6 //时空复杂度: O(n*len)(len为单词平均长度)
  7 //copyright@yansha 2011.10.25
  8 //updated@July 2011.10.26
  9 //程序尚不完善，有很多地方还需改进。
 10 #include <stdio.h>
 11 #include <stdlib.h>
 12 #include <string.h>
 13 #include <ctype.h>
 14 #include <assert.h>
 15 
 16 #define num_of_letters 26
 17 #define max_word_length 20
 18 
 19 // 定义trie树节点
 20 struct Trie   
 21 {   
 22   int count;   
 23   Trie *next[num_of_letters]; 
 24 };   
 25 
 26 // 定义根节点 
 27 Trie *root = NULL;
 28 
 29 /**
 30 * 建立trie树，同时保存单词频率
 31 */
 32 void create_trie(char *word)
 33 {
 34   int len = strlen(word);
 35   Trie *cur = root, *node;
 36   int pos = 0;
 37 
 38   // 深度为单词长度
 39   for(int i = 0; i < len; ++i)
 40   {
 41     // 将字母范围映射到0-25之间
 42     pos = word[i] - 'a';
 43 
 44     // 如果当前字母没有对应的trie树节点则建立，否则处理下一个字母
 45     if(cur->next[pos] == NULL)   //1、这里应该有个查找过程
 46     {
 47       node = (Trie *)malloc(sizeof(Trie));
 48       node->count = 0;
 49 
 50       // 初始化next节点
 51       for(int j = 0; j < num_of_letters; ++j)
 52       node->next[j] = NULL;
 53 
 54       // 开始处理下一个字母
 55       cur->next[pos] = node;
 56       }
 57   cur = cur->next[pos];
 58   }
 59   // 单词频率加1
 60   cur->count++;
 61 }
 62 
 63 /**
 64 * 大写字母转化成小写字母
 65 */
 66 void upper_to_lower(char *word, int len)
 67 {
 68   for (int i = 0; i < len; ++i)
 69   {
 70     if(word[i] >= 'A' && word[i] <= 'Z')
 71     word[i] += 32;
 72   }
 73 }
 74 
 75 /**
 76 * 处理输入
 77 */
 78 void process_input()
 79 {
 80   char word[max_word_length];
 81 
 82   // 打开统计文件(注意保持文件名一致)
 83   FILE *fp_passage = fopen("passage.txt", "r");  
 84   assert(fp_passage);
 85 
 86   // 循环处理单词
 87   while (fscanf(fp_passage, "%s", word) != EOF)  
 88   {  
 89     int len = strlen(word);  
 90     if (len > 0)  
 91       upper_to_lower(word, len);  
 92     create_trie(word);  
 93   }  
 94   fclose(fp_passage);  
 95 }
 96 
 97 /**
 98 * 深度优先遍历
 99 */ 
100 void trie_dfs(Trie *p, char *queue)
101 {
102   for(int i = 0; i < num_of_letters; ++i)
103   {
104     if(p->next[i] != NULL)
105   {
106     // 定义队列头结点
107     char *head = queue;
108 
109     // 在末尾增加一个字母
110     while (*queue != '')
111       queue++;
112     *queue = (char)(i + 'a');
113     queue = head;
114 
115     // 在控制台打印单词及其频率
116     if (p->next[i]->count > 0)
117       printf("%s	%d
", queue, p->next[i]->count);
118 
119     trie_dfs(p->next[i], queue);
120 
121     // 在末尾去掉一个字母
122     head = queue;
123     while (*(queue+1) != '')
124       queue++;
125     *queue = '';
126     queue = head;
127     }
128   }
129 }
130 
131 int main()
132 {
133   // 初始化trie树根节点
134   root = (Trie *)malloc(sizeof(Trie));
135   for(int j = 0; j < num_of_letters; ++j)
136   root->next[j] = NULL;
137 
138   // 处理输入
139   process_input();
140 
141   // 分配一个保存单词中间结果的队列
142   char *queue = (char*) calloc(max_word_length, sizeof(char));
143 
144   // 通过DFS打印结果
145   trie_dfs(root, queue);
146   system("pause");
147   return 0;
148 }

View Code

　　2.后缀树

　　1).简介

　　后缀，顾名思义，甚至通俗点来说，就是所谓后缀就是后面尾巴的意思。比如说给定一长度为n的字符串S=S1S2..Si..Sn，和整数i，1 <= i <= n，子串SiSi+1...Sn便都是字符串S的后缀。

　　以字符串S=XMADAMYX为例，它的长度为8，所以S[1..8], S[2..8], ... , S[8..8]都算S的后缀，我们一般还把空字串也算成后缀。这样，我们一共有如下后缀。对于后缀S[i..n]，我们说这项后缀起始于i。

S[1..8], XMADAMYX，也就是字符串本身，起始位置为1
  S[2..8], MADAMYX，起始位置为2
     S[3..8], ADAMYX，起始位置为3
       S[4..8], DAMYX，起始位置为4
          S[5..8], AMYX，起始位置为5
            S[6..8], MYX，起始位置为6
               S[7..8], YX，起始位置为7
                 S[8..8], X，起始位置为8
                                 空字串，记为$。

而后缀树，就是包含一则字符串所有后缀的压缩Trie(关键在于压缩)。把上面的后缀加入Trie后，我们得到下面的结构：

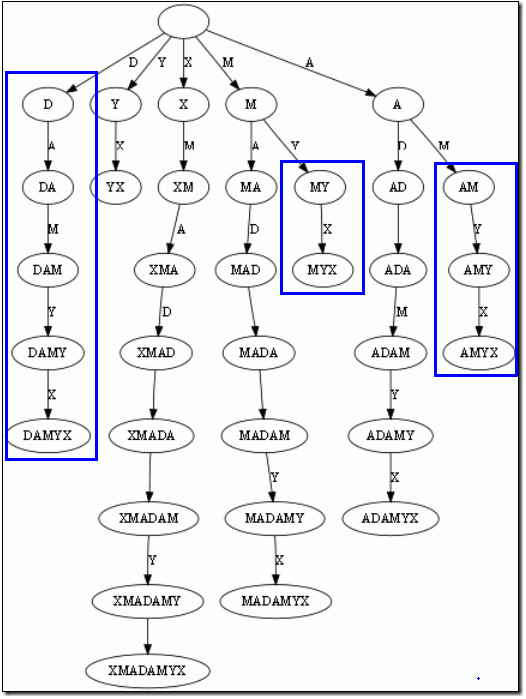
　　仔细观察上图，我们可以看到不少值得压缩的地方。比如蓝框标注的分支都是独苗，没有必要用单独的节点同边表示。如果我们允许任意一条边里包含多个字母，就可以把这种没有分叉的路径压缩到一条边。另外每条边已经包含了足够的后缀信息，我们就不用再给节点标注字符串信息了。我们只需要在叶节点上标注上每项后缀的起始位置。于是我们得到下图：

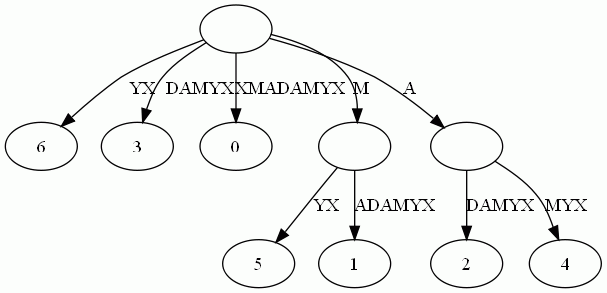
　　这样的结构丢失了某些后缀。比如后缀X在上图中消失了，因为它正好是字符串XMADAMYX的前缀。为了避免这种情况，我们也规定每项后缀不能是其它后缀的前缀。要解决这个问题其实挺简单，在待处理的子串后加一个空字串就行了。例如我们处理XMADAMYX前，先把XMADAMYX变为 XMADAMYX$，于是就得到suffix tree--后缀树了，如下图所示：

　　2).回文串

　　找出给定字符串里的最长回文。例如输入XMADAMYX，则输出MADAM。

　　思维的突破点在于考察回文的半径，而不是回文本身。所谓半径，就是回文对折后的字串。比如回文MADAM 的半径为MAD，半径长度为3，半径的中心是字母D。显然，最长回文必有最长半径，且两条半径相等。还是以MADAM为例，以D为中心往左，我们得到半径 DAM；以D为中心向右，我们得到半径DAM。二者肯定相等。因为MADAM已经是单词XMADAMYX里的最长回文，我们可以肯定从D往左数的字串 DAMX与从D往右数的子串DAMYX共享最长前缀DAM。而这，正是解决回文问题的关键。现在我们有后缀树，怎么把从D向左数的字串DAMX变成后缀呢？

　　到这个地步，答案应该明显：把单词XMADAMYX翻转（XMADAMYX=>XYMADAMX，DAMX就变成后缀了）就行了。于是我们把寻找回文的问题转换成了寻找两坨后缀的LCA的问题。当然，我们还需要知道到底查询那些后缀间的LCA。很简单，给定字符串S，如果最长回文的中心在i，那从位置i向右数的后缀刚好是S(i)，而向左数的字符串刚好是翻转S后得到的字符串S‘的后缀S'(n-i+1)。这里的n是字符串S的长度。

　　最低共有祖先，LCA（Lowest Common Ancestor)，也就是任意两节点（多个也行）最长的共有前缀。

　　算法：

预处理后缀树，使得查询LCA的复杂度为O(1)。这步的开销是O(N)，N是单词S的长度；
对单词的每一位置i(也就是从0到N-1)，获取LCA(S(i), S‘(N-i+1)) 以及LCA(S(i+1), S’(n-i+1))。查找两次的原因是我们需要考虑奇数回文和偶数回文的情况。这步要考察每坨i，所以复杂度是O(N) ；
找到最大的LCA，我们也就得到了回文的中心i以及回文的半径长度，自然也就得到了最长回文。总的复杂度O(n)。

　　3)后缀树应用

查找字符串o是否在字符串S中。
方案：用S构造后缀树，按在trie中搜索字串的方法搜索o即可。
原理：若o在S中，则o必然是S的某个后缀的前缀。
例如S: leconte，查找o: con是否在S中,则o(con)必然是S(leconte)的后缀之一conte的前缀.有了这个前提，采用trie搜索的方法就不难理解了。。
指定字符串T在字符串S中的重复次数。
方案：用S+’$'构造后缀树，搜索T节点下的叶节点数目即为重复次数
原理：如果T在S中重复了两次，则S应有两个后缀以T为前缀，重复次数就自然统计出来了。。
字符串S中的最长重复子串
  方案一：列出所有后缀数组。对其首字母排序，
  　　对数组进行扫描比较邻接元素，取出最多相同邻接元素的子字符串，保存那个字符串和长度。
方案二：原理同2，具体做法就是找到最深的非叶节点。
  这个深是指从root所经历过的字符个数，最深非叶节点所经历的字符串起来就是最长重复子串。
为什么要非叶节点呢?因为既然是要重复，当然叶节点个数要>=2。
两个字符串S1，S2的最长公共部分
方案：将S1#S2$作为字符串压入后缀树，找到最深的非叶节点，且该节点的叶节点既有#也有$(无#)。

　　3.自动机，KMP算法，Extend-KMP，后缀树，后缀数组，trie树，trie图及其应用

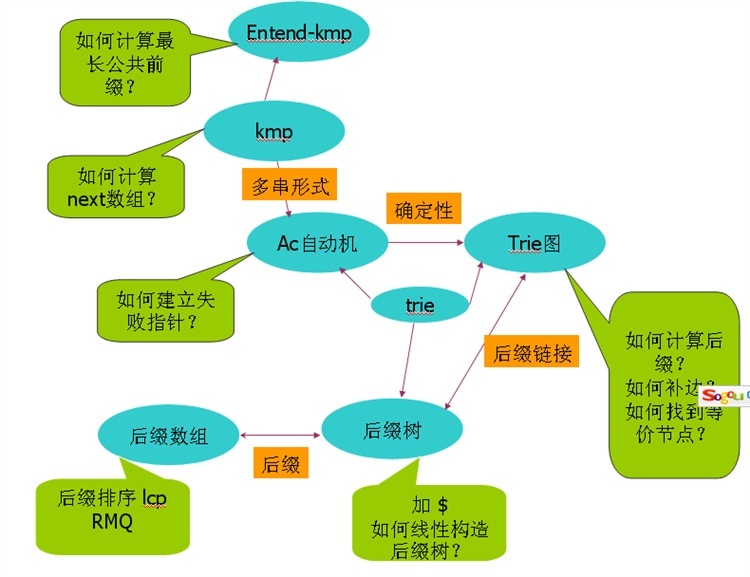
kmp

   首先这个字符串匹配算法，主要思想就是要充分利用上一次的匹配结果，找到匹配失败时，模式串可以向前移动的最大距离。这个最大距离，必须要保证不会错过可能的匹配位置，因此这个最大距离实际上就是模式串当前匹配位置的next数组值。也就是max{Aj 是 Pi 的后缀  j < i}，pi表示字符串A[1...i],Aj表示A[1...j]。模式串的next数组计算则是一个自匹配的过程。也是利用已有值next[1...i-1]计算next[i]的过程。我们可以看到，如果A[i] = A[next[i-1]+1] 那么next[i] = next[i-1]，否则，就可以将模式串继续前移了。
整个过程是这样的：
void next_comp(char * str){
   int next[N+1];
   int k = 0;
   next[1] = 0;
   //循环不变性，每次循环的开始，k = next[i-1]
   for(int i = 2 ; i <= N ; i++){
      //如果当前位置不匹配，或者还推进到字符串开始，则继续推进
      while(A[k+1] != A[i] && k != 0){
           k = next[k];
      }
      if(A[k+1] == A[i]) k++;
      next[i] = k;
   }
}
   复杂度分析：从上面的过程可以看出，内部循环再不断的执行k = next[k]，而这个值必然是在缩小，也就是是没执行一次k至少减少1；另一方面k的初值是0，而最多++ N次，而k始终保持非负，很明显减少的不可能大于增加的那些，所以整个过程的复杂度是O(N)。
   上面是next数组的计算过程，而整个kmp的匹配过程与此类似。

extend-kmp

   为什么叫做扩展-kmp呢，首先我们看它计算的内容，它是要求出字符串B的后缀与字符串A的最长公共前缀。extend[i]表示B[i...B_len] 与A的最长公共前缀长度，也就是要计算这个数组。观察这个数组可以知道，kmp可以判断A是否是B的一个子串，并且找到第一个匹配位置？而对于extend[]数组来说，则可以利用它直接解决匹配问题，只要看extend[]数组元素是否有一个等于len_A即可。显然这个数组保存了更多更丰富的信息，即B的每个位置与A的匹配长度。
   计算这个数组extend也采用了于kmp类似的过程。首先也是需要计算字符串A与自身后缀的最长公共前缀长度。我们设为next[]数组。当然这里next数组的含义与kmp里的有所过程。但它的计算，也是利用了已经计算出来的next[1...i-1]来找到next[i]的大小，整体的思路是一样的。
   具体是这样的：观察下图可以发现

首先在1...i-1,要找到一个k，使得它满足k+next[k]-1最大，也就是说，让k加上next[k]长度尽量长。实际上下面的证明过程中就是利用了每次计算后k+next[k]始终只增不减，而它很明显有个上界，来证明整个计算过程复杂度是线性的。如下图所示，假设我们已经找到这样的k，然后看怎么计算next[i]的值。设len = k+next[k]-1(图中我们用Ak代表next[k]),分情况讨论：

如果len < i 也就是说，len的长度还未覆盖到Ai,这样我们只要从头开始比较A[i...n]与A的最长公共前缀即可，这种情况下很明显的，每比较一次，必然就会让i+next[i]-1增加一.
如果len >= i,就是我们在图中表达的情形，这时我们可以看到i这个位置现在等于i-k+1这个位置的元素，这样又分两种情况：

如果 L = next[i-k+1] >= len-i+1,也就是说L处在第二条虚线的位置，这样我们可以看到next[i]的大小，至少是len-i+1,然后我们再从此处开始比较后面的还能否匹配，显然如果多比较一次，也会让i+A[i]-1多增加1.
如果 L < len-i+1 也就是说L处在第一条虚线位置，我们知道A与Ak在这个位置匹配，但Ak与Ai-k+1在这个位置不匹配，显然A与与Ai-k+1在这个位置也不会匹配，故next[i]的值就是L。这样next[i]的值就被计算出来了，从上面的过程中我们可以看到，next[i]要么可以直接由k这个位置计算出来，要么需要在逐个比较，但是如果需要比较，则每次比较会让k+next[k]-1的最大值加1.而整个过程中这个值只增不减，而且它有一个很明显的上界k+next[k]-1 < 2*len_A,可见比较的次数要被限制到这个数值之内，因此总的复杂度将是O(N)的。

参考：http://www.cnblogs.com/v-July-v/archive/2011/10/22/2316412.html

百度百科