作者:jostree 转载请注明出处 http://www.cnblogs.com/jostree/p/4397990.html
在机器学习中,求凸函数的极值是一个常见的问题,常见的方法如梯度下降法,牛顿法等,今天我们介绍一种三分法来求一个凸函数的极值问题。
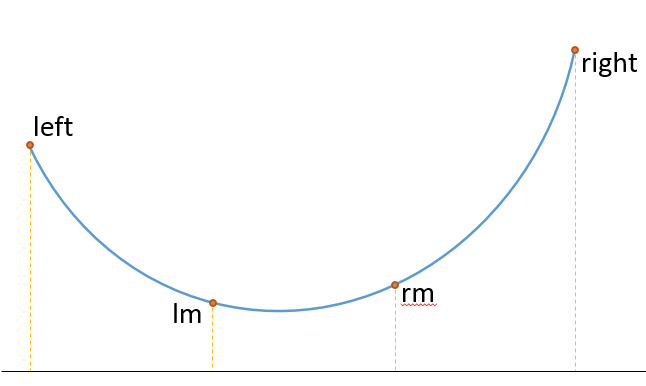
对于如下图的一个凸函数$f(x),xin [left,right]$,其中lm和rm分别为区间[left,right]的三等分点,我们发现如果f(lm)<f(rm),那么函数值最小的点的横坐标x一定在[left,rm]之间。如果x在[rm,right]之间,就会出现在rm左右都有比他低的点,这显然是不可能的。 同理,当f(lm)>f(rm)时,最值的横坐标x一定在[lm,right]的区间内。
利用这个性质,我们就可以在缩小区间的同时向目标点逼近,从而得到极值。
举一个例子,题目源自http://hihocoder.com/contest/hiho40/problem/1,如下图在直角坐标系中有一条抛物线y=ax^2+bx+c和一个点P(x,y),求点P到抛物线的最短距离d,其中-200≤a,b,c,x,y≤200。我们另pivot代表抛物线的对称抽,可以发现当X>pivot,我们可以取left = pivot,right = inf, 反之left = -inf , right = pivot, 其距离恰好满足凸形函数。而我们要求的最短距离d,正好就是这个凸形函数的极值。

代码如下:
#include <stdlib.h> #include <stdio.h> #include <string.h> #include <limits.h> #include <iostream> #include <cmath> using namespace std; double a, b, c, x, y; const double MAX = 100000; double dis(double X) { double Y = a*X*X+b*X+c; return sqrt((x-X)*(x-X)+(y-Y)*(y-Y)); } double solve(double l, double r) { double lm = l + (r-l)/3; double rm = r - (r-l)/3; double lmd = dis(lm); double rmd = dis(rm); if( fabs(lmd - rmd) < 0.0001 ) { return lmd; } if( lmd > rmd ) { return solve(lm, r); } else { return solve(l, rm); } } int main(int argc, char *argv[]) { while( cin>>a>>b>>c>>x>>y ) { double pivot = -b/(2*a); double l = 0, r = 0; if( pivot < x ) { l = pivot + 0.0001; r = MAX; } else { l = -MAX; r = pivot - 0.0001; } double res = solve(l, r); printf("%.3lf ", res); } }