前置芝士:二分图
先介绍一下什么是二分图:
二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。
——百度百科
有点难懂?就是说把一个图中的点分成两部分,每一部分中的点内两两没有连边,分开之后的图就叫二分图。
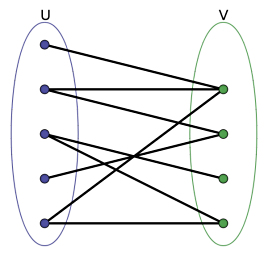
如图:
上主菜:二分图匹配
概念:给定一个二分图G,在G的一个子图M中,M的边集{E}中的任意两条边都不依附于同一个顶点,则称M是一个匹配。
接下来就是如何匹配了——匈牙利算法(本蒟蒻只会这个啦
匈牙利算法简单来说其实就是一个绿与被绿的过程。
我就不用什么增广路等专业术语了,反正考场上又不是问我们这个叫什么。
懒得画图了,就拿百度百科那张图来吧。
不妨设(U)中节点从上往下为(U=left{1,2,3,4,5
ight}),同时(V=left{6,7,8,9
ight})
首先是(1)号点,找到(6)并与它完成匹配,继续是(2)号点,也有一条边连向(6),但发现(6)已经被匹配,所以就找(6)还有没有其他点可以匹配,却没有,所以就找已经与(6)匹配的点(1),(1)也被匹配了,重复以上操作,发现除了(6)没有其他点,说明(2)不能与(6)匹配,因此找到下一个点(7),与之匹配。
然后就是不断重复以上操作,直到枚举完为止。我们其实可以发现这是一个递归的过程,所以用DFS就可以啦!
代码因本人丑陋的码风就不贴了,网上代码满天飞,其实也可以自己想想该怎么实现。
咱门继续下一个:
树链剖分
这种数据结构很适合码农来打
当我们遇到类似树上求一条链(x-y)的点值总和时,就会聪明的进行一次预处理,然后(ans=sum[x]+sum[y]-sum[lca]-sum[fa[lca]])
但如果有修改操作呢?这种方式就行不通了,所以只能引入一个新的数据结构:树链剖分。
主要基操 (我基本不会的操作:将树上的修改转移到树的DFS序上
首先维护一个数组(son[u]),表示(u)的重儿子,也就是节点数最大的那个儿子节点,同时需要(size[u],dep[u],fa[u],dfn[u],id[x]),前三个应该不用说了吧?(dfn[u])表示(u)节点在DFS序中的下标,(id[x])则是在DFS序中下标为(x)的节点。
预处理:两遍DFS:
第一遍DFS处理的是重儿子,为什么不一起处理呢?因为我们要保证DFS序中一个节点与它的重儿子在一起,所以要先处理重儿子数组。第二遍DFS就是处理DFS序了。代码如下:
void dfs1(int u,int fat)
{
size[u]=1;
for(re int v,i=hd[u];i;i=e[i].net)
{
v=e[i].v;
if(v==fat)continue;
fa[v]=u,dep[v]=dep[u]+1;
dfs1(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]])son[u]=v;
}
}
void dfs2(int u,int fat)
{
dfn[u]=++cnt,id[cnt]=u,top[u]=fat;
if(son[u]==0)return ;
dfs2(son[u],fat);//保证它与它的重儿子在一起
for(re int v,i=hd[u];i;i=e[i].net)
{
v=e[i].v;
if(v==fa[u]||v==son[u])continue;
dfs2(v,v);
}
}
然后就用线段树,树状数组等在DFS序上乱搞就行了。
模板例题:P3384 轻重链剖分
这题与上面的问题差不多,多了一个子树处理,稍微提示一下:一个节点与它的子树节点的DFS序靠在一起,所以可以思考一下。
手起,码落:
#include<bits/stdc++.h>
#define re register
using namespace std;
inline int read()
{
re int x=0,f=1;
re char ch=getchar();
for(;ch>'9'||ch<'0';ch=getchar())if(ch=='-')f*=-1;
for(;ch>='0'&&ch<='9';ch=getchar())x=(x<<1)+(x<<3)+(ch^48);
return x*f;
}
const int N=100005;
struct edge{int v,net;}e[N<<1];
struct tree{int l,r,val,lazy;}t[N<<3];
int n,m,cnt,a[N],hd[N],dfn[N],top[N],son[N],mod,dep[N],size[N],fa[N],id[N],rt;
inline void ad(int v,int u)
{
e[++cnt].v=v,e[cnt].net=hd[u],hd[u]=cnt;
e[++cnt].v=u,e[cnt].net=hd[v],hd[v]=cnt;
}
void dfs1(int u,int fat)
{
size[u]=1;
for(re int v,i=hd[u];i;i=e[i].net)
{
v=e[i].v;
if(v==fat)continue;
fa[v]=u,dep[v]=dep[u]+1;
dfs1(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]])son[u]=v;
}
}
void dfs2(int u,int fat)
{
dfn[u]=++cnt,id[cnt]=u,top[u]=fat;
if(son[u]==0)return ;
dfs2(son[u],fat);
for(re int v,i=hd[u];i;i=e[i].net)
{
v=e[i].v;
if(v==fa[u]||v==son[u])continue;
dfs2(v,v);
}
}
inline void Down(int x)
{
if(t[x].lazy)
{
(t[x<<1].lazy+=t[x].lazy)%=mod,(t[x<<1|1].lazy+=t[x].lazy)%=mod;
(t[x<<1].val+=t[x].lazy*(t[x<<1].r-t[x<<1].l+1)%mod)%=mod,(t[x<<1|1].val+=t[x].lazy*(t[x<<1|1].r-t[x<<1|1].l+1)%mod)%=mod;
t[x].lazy=0;
}
}
int query(int l,int r,int x)
{
if(l<=t[x].l&&t[x].r<=r)return t[x].val;
Down(x);
re int sum=0;
if(t[x<<1].r>=l)(sum+=query(l,r,x<<1))%=mod;
if(t[x<<1|1].l<=r)(sum+=query(l,r,x<<1|1))%=mod;
return sum%mod;
}
void add(int l,int r,int x,int val)
{
if(l<=t[x].l&&t[x].r<=r)
{
(t[x].lazy+=val)%=mod,(t[x].val+=val*(t[x].r-t[x].l+1)%mod)%=mod;
return ;
}
Down(x);
if(t[x<<1].r>=l)add(l,r,x<<1,val);
if(t[x<<1|1].l<=r)add(l,r,x<<1|1,val);
t[x].val=(t[x<<1].val+t[x<<1|1].val)%mod;
}
inline void query_add(int x,int y,int val)
{
re int fx=top[x],fy=top[y];
for(;fx^fy;)
{
if(dep[fx]>=dep[fy])
{
add(dfn[fx],dfn[x],1,val);
x=fa[fx],fx=top[x];
}
else
{
add(dfn[fy],dfn[y],1,val);
y=fa[fy],fy=top[y];
}
}
if(dfn[x]<dfn[y])add(dfn[x],dfn[y],1,val);
else add(dfn[y],dfn[x],1,val);
}
inline int query_sum(int x,int y)
{
re int fx=top[x],fy=top[y],sum=0;
for(;fx^fy;)
{
if(dep[fx]>=dep[fy])
{
(sum+=query(dfn[fx],dfn[x],1))%=mod;
x=fa[fx],fx=top[x];
}
else
{
(sum+=query(dfn[fy],dfn[y],1))%=mod;
y=fa[fy],fy=top[y];
}
}
if(dfn[x]<dfn[y])(sum+=query(dfn[x],dfn[y],1))%=mod;
else (sum+=query(dfn[y],dfn[x],1))%=mod;
return sum;
}
void build(int l,int r,int x)
{
t[x].l=l,t[x].r=r;
if(l>r)return ;
else if(l==r)
{
t[x].val=a[id[l]];
return ;
}
re int mid=(l+r)>>1;
build(l,mid,x<<1);
build(mid+1,r,x<<1|1);
t[x].val=(t[x<<1].val+t[x<<1|1].val)%mod;
}
int main()
{
n=read(),m=read(),rt=read(),mod=read();
for(re int i=1;i<=n;i++)a[i]=read();
for(re int i=1;i<n;i++)ad(read(),read());
cnt=0,dfs1(rt,0),dfs2(rt,rt),build(1,n,1);
for(re int type,x,y,z,i=1;i<=m;i++)
{
type=read(),x=read();
if(type==1)
{
y=read(),z=read();
query_add(x,y,z);
}
else if(type==2)
{
y=read();
printf("%d
",query_sum(x,y));
}
else if(type==3)
{
z=read();
add(dfn[x],dfn[x]+size[x]-1,1,z);
}
else printf("%d
",query(dfn[x],dfn[x]+size[x]-1,1));
}
return 0;
}
