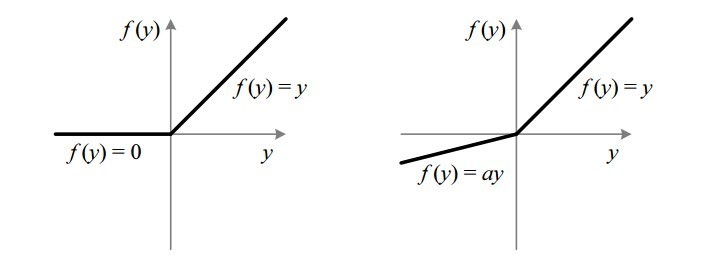梯度消失与梯度爆炸
梯度为偏导数构成的向量。
损失函数收敛至极小值时,梯度为0(接近0),损失函数不再下降。我们不希望在抵达极小值前,梯度就为0了,也不希望下降过程过于震荡,甚至不收敛。梯度消失与梯度爆炸分别对应这2种现象,
梯度消失(vanishing gradients):指的是在训练过程中,梯度(偏导)过早接近于0的现象,导致(部分)参数一直不再更新,整体上表现得像损失函数收敛了,实际上网络尚未得到充分的训练。
梯度爆炸(exploding gradients):指的是在训练过程中,梯度(偏导)过大甚至为NAN(not a number)的现象,导致损失剧烈震荡,甚至发散(divergence)。
由上一节的分析可知,在梯度(偏导)计算中,主要的影响因素来自激活函数的偏导、当前层的输入(前一层的输出)、以及权重的数值等,这些因子连续相乘,带来的影响是指数级的。训练阶段,权重在不断调整,每一层的输入输出也在不断变化,梯度消失和梯度爆炸可能发生在训练的一开始、也可能发生在训练的过程中。
因子项中当前层的输入仅出现一次,下面着重看一下激活函数和权重的影响。
激活函数的影响
以Sigmoid和Tanh为例,其函数与导数如下(来自链接),
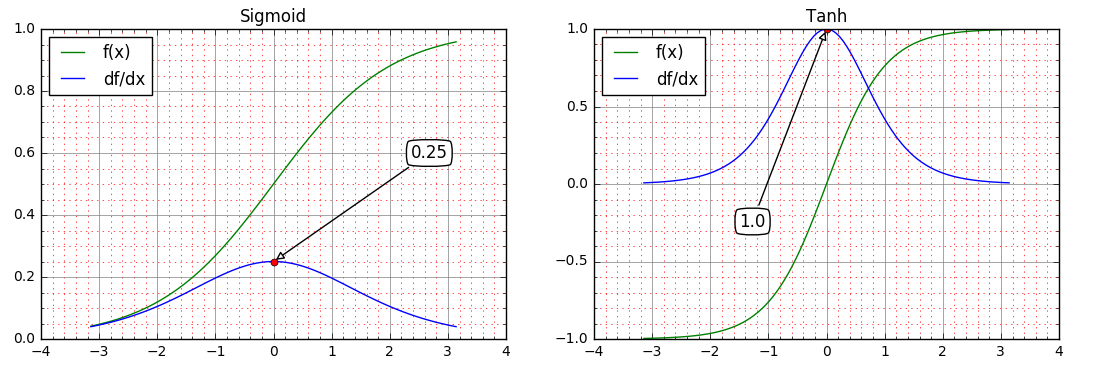 Sigmoid和Tanh,及其导数
Sigmoid和Tanh,及其导数
两者的导数均在原点处取得最大值,前者为0.25后者为1,在远离原点的正负方向上,两者导数均趋近于0,即存在饱和区。
- 原点附近:从因子项连乘结果看,Tanh比Sigmoid稍好,其在原点附近的导数在1附近,如果激活函数的输入均在0左右,偏导连续相乘不会很小也不会很大。而sigmoid就会比较糟糕,其导数最大值为0.25,连续相乘会使梯度指数级减小,在反向传播时,对层数越多的网络,浅层的梯度消失现象越明显。
- 饱和区:一旦陷入饱和区,两者的偏导都接近于0,导致权重的更新量很小,比如某些权重很大,导致相关的神经元一直陷在饱和区,更新量又接近于0,以致很难跳出或者要花费很长时间才能跳出饱和区。
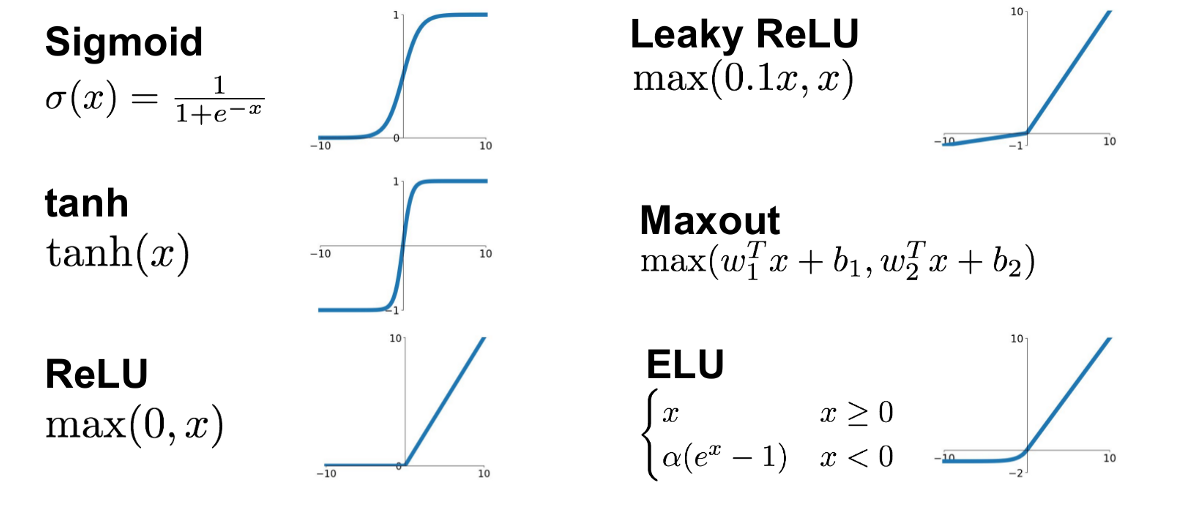
所以,一个改善方向是选择更好的非线性激活函数,比如ReLU,相关激活函数如下图所示,
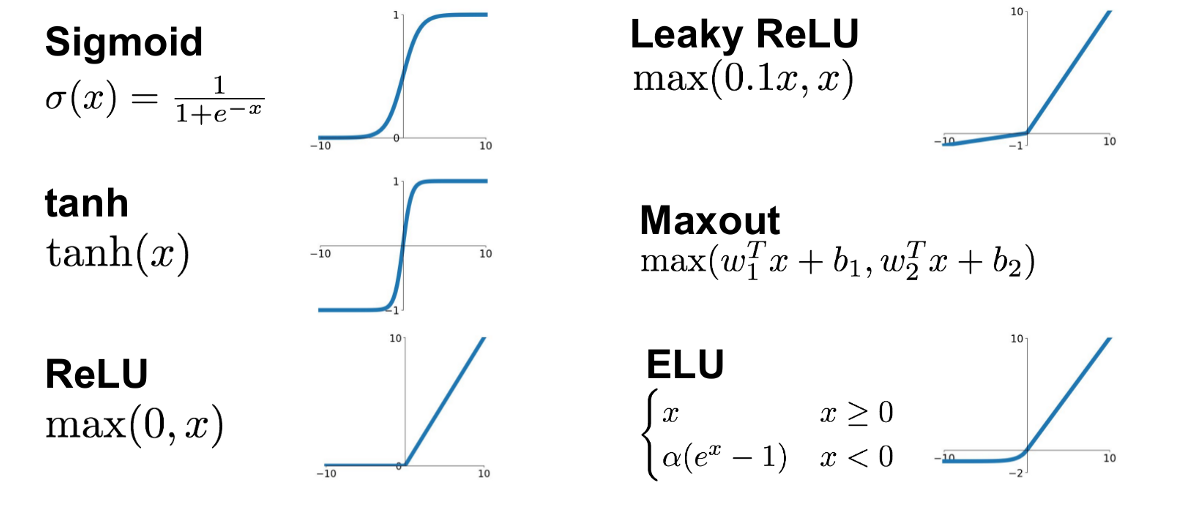 activation functions
activation functions
ReLU只在负方向上存在饱和区,正方向上的导数均为1,因此相对更少地遭遇梯度消失,但梯度爆炸现象仍然存在。
权重矩阵的影响
假设激活函数为线性,就像ReLU的正向部分,导数全为1。则一个简化版本的全连接神经网络如下图所示,
 a simple 9-layer neural network
a simple 9-layer neural network
假设权重矩阵均为WW,前向传播和反向传播过程均涉及WW(转置)的反复相乘,tt步相当于WtWt,若WW有特征值分解W=V diag(λ) V−1W=V diag(λ) V−1,简单地,
其中diag(λ)diag(λ)为特征值对角矩阵,如果特征值λiλi不在1附近,大于1经过tt次幂后会“爆炸”,小于1经过tt次幂后会“消失”。
如果网络初始化时,权重矩阵过小或过大,则在网络训练的初始阶段就可能遭遇梯度消失或梯度爆炸,表现为损失函数不下降或者过于震荡。
不良初始化
至此,一些权重不良初始化导致的问题就不难解释了,
- 过小,导致梯度消失
- 过大,导致梯度爆炸
- 全常数初始化,即所有权重WW都相同,则z(2)=W1xz(2)=W1x相同,导致后面每一层的输入和输出均相同,即aa和zz相同,回到反向传播的公式,每层的偏导相同,进一步导致每层的权重会向相同的方向同步更新,如果学习率只有一个,则每层更新后的权重仍然相同,每层的效果等价于一个神经元,这无疑极大限制了网络的能力。

反向传播中的偏导计算
- 特别地,全0初始化,根据上式,如果激活函数g(0)=0g(0)=0,如ReLU,则初始状态所有激活函数的输入zz和输出aa都为0,反向传播时所有的梯度为0,权重不会更新,一直保持为0;如果激活函数g(0)≠0g(0)≠0,则初始状态激活层的输入为0,但输出a≠0a≠0,则权重会从最后一层开始逐层向前更新,改变全0的状态,但是每层权重的更新方向仍相同,同上。
全0、常数、过大、过小的权重初始化都是不好的,那我们需要什么样的初始化?
- 因为对权重ww的大小和正负缺乏先验,所以应初始化在0附近,但不能为全0或常数,所以要有一定的随机性,即数学期望E(w)=0E(w)=0;
- 因为梯度消失和梯度爆炸,权重不易过大或过小,所以要对权重的方差Var(w)Var(w)有所控制;
- 深度神经网络的多层结构中,每个激活层的输出对后面的层而言都是输入,所以我们希望不同激活层输出的方差相同,即Var(a[l])=Var(a[l−1])Var(a[l])=Var(a[l−1]),这也就意味不同激活层输入的方差相同,即Var(z[l])=Var(z[l−1])Var(z[l])=Var(z[l−1]);
- 如果忽略激活函数,前向传播和反向传播可以看成是权重矩阵(转置)的连续相乘。数值太大,前向时可能陷入饱和区,反向时可能梯度爆炸,数值太小,反向时可能梯度消失。所以初始化时,权重的数值范围(方差)应考虑到前向和后向两个过程;
权重的随机初始化过程可以看成是从某个概率分布随机采样的过程,常用的分布有高斯分布、均匀分布等,对权重期望和方差的控制可转化为概率分布的参数控制,权重初始化问题也就变成了概率分布的参数设置问题。
在上回中,我们知道反向传播过程同时受到权重矩阵和激活函数的影响,那么,在激活函数不同以及每层超参数配置不同(输入输出数量)的情况下,权重初始化该做怎样的适配?这里,将各家的研究成果汇总如下,
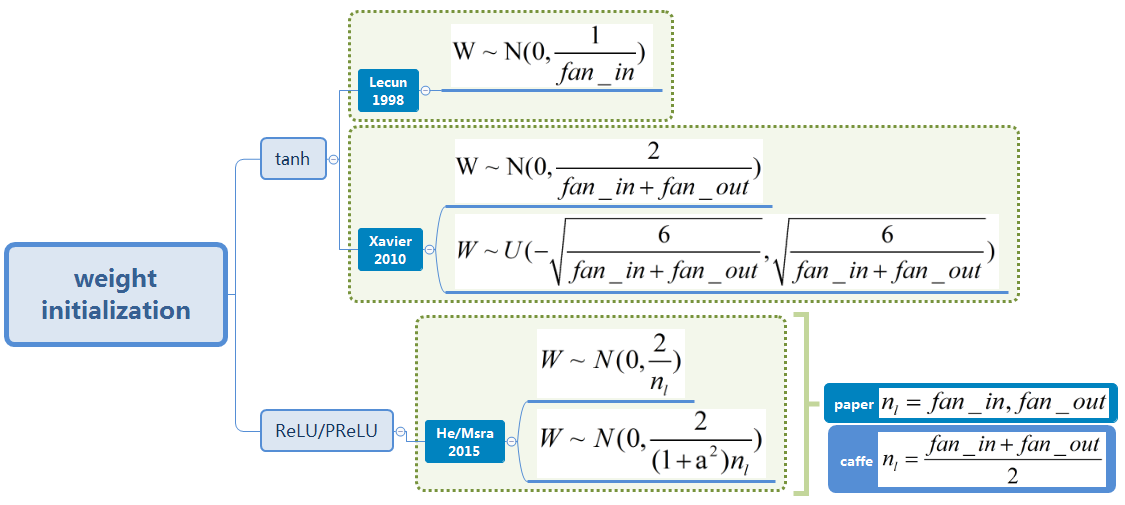 weight initialization
weight initialization
其中,扇入fan–infan_in和扇出fan–outfan_out分别为当前全连接层的输入和输出数量,更准确地说,1个输出神经元与fan–infan_in个输入神经元有连接(the number of connections feeding into the node),1个输入神经元与fan–outfan_out个输出神经元有连接(the number of connections flowing out of the node),如下图所示(来自链接),
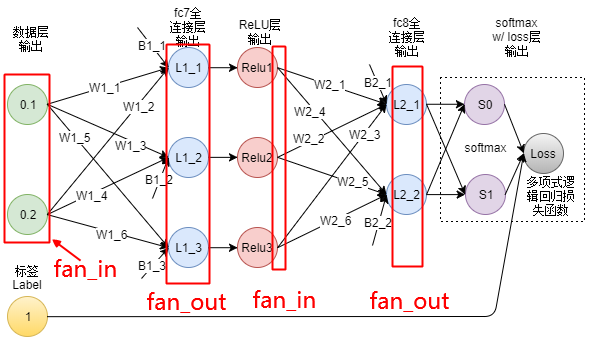
对于卷积层而言,其权重为nn个c×h×wc×h×w大小的卷积核,则一个输出神经元与c×h×wc×h×w个输入神经元有连接,即fan–in=c×h×wfan_in=c×h×w,一个输入神经元与n×h×wn×h×w个输出神经元有连接,即fan–out=n×h×wfan_out=n×h×w。
期望与方差的相关性质
接下来,首先回顾一下期望与方差计算的相关性质。
对于随机变量XX,其方差可通过下式计算,
若两个随机变量XX和YY,它们相互独立,则其协方差为0,
进一步可得E(XY)=E(X)E(Y)E(XY)=E(X)E(Y),推导如下,
两个独立随机变量和的方差,
两个独立随机变量积的方差,
全连接层方差分析

在初始化阶段,将每个权重以及每个输入视为随机变量,可做如下假设和推断,
- 网络输入的每个元素x1,x2,…x1,x2,…为独立同分布;
- 每层的权重随机初始化,同层的权重wi1,wi2,…wi1,wi2,…独立同分布,且期望E(w)=0E(w)=0;
- 每层的权重ww和输入aa随机初始化且相互独立,所以两者之积构成的随机变量wi1a1,wi2a2,…wi1a1,wi2a2,…亦相互独立,且同分布;
- 根据上面的计算公式,同层的z1,z2,…z1,z2,…为独立同分布,同层的a1,a2,…a1,a2,…也为独立同分布;
需要注意的是,上面独立同分布的假设仅在初始化阶段成立,当网络开始训练,根据反向传播公式,权重更新后不再相互独立。

tanh下的初始化方法

为了避免梯度消失和梯度爆炸,最好保持这个系数为1。
需要注意的是,上面的结论是在激活函数为恒等映射的条件下得出的,而tanh激活函数在0附近可近似为恒等映射,即tanh(x)≈xtanh(x)≈x。
Lecun 1998

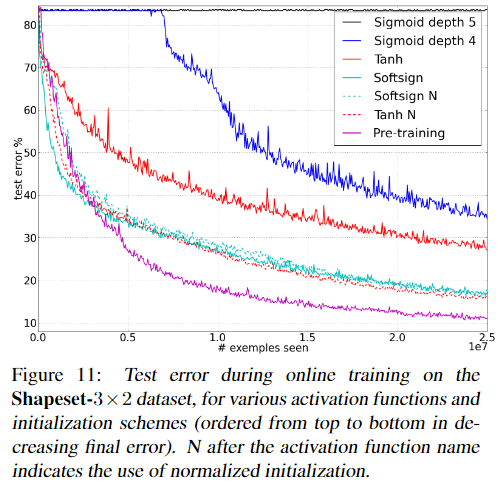
Xavier 2010

论文还有更多训练过程中的权重和梯度对比图示,这里不再贴出,具体可以参见论文。
ReLU/PReLU下的初始化方法

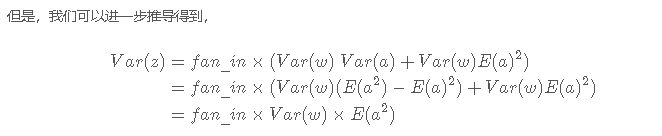
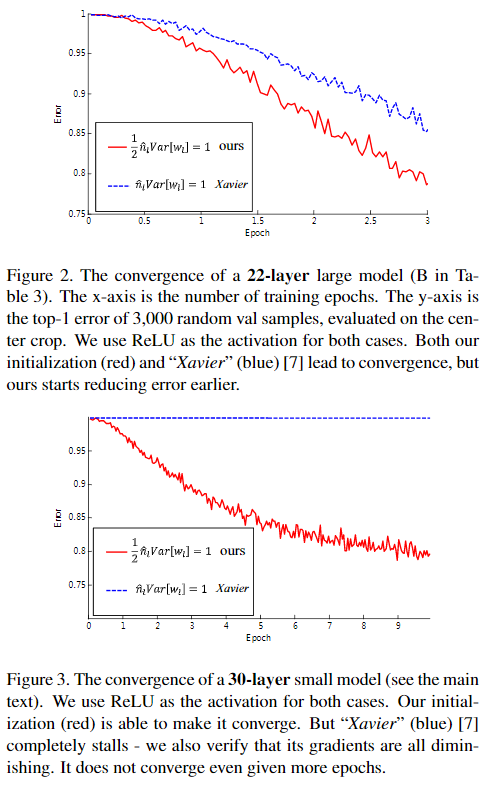
He 2015 for ReLU


使用Xavier和He初始化,在激活函数为ReLU的情况下,test error下降对比如下,22层的网络,He的初始化下降更快,30层的网络,Xavier不下降,但是He正常下降。
He 2015 for PReLU
对于PReLU激活函数,负向部分为f(x)=axf(x)=ax,如下右所示,
ReLU and PReLU

小结
至此,对深度神经网络权重初始化方法的介绍已告一段落。虽然因为BN层的提出,权重初始化可能已不再那么紧要。但是,对经典权重初始化方法经过一番剖析后,相信对神经网络运行机制的理解也会更加深刻。
以上。
参考
- cs231n-Neural Networks Part 2: Setting up the Data and the Loss
- paper-Efficient BackProp
- paper-Understanding the difficulty of training deep feedforward neural networks
- paper-Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification
- wiki-Variance
- Initializing neural networks
- Weight Initialization in Neural Networks: A Journey From the Basics to Kaiming
- Kaiming He initialization
- Choosing Weights: Small Changes, Big Differences
- Understand Kaiming Initialization and Implementation Detail in PyTorch