// 此博文为迁移而来,写于2015年4月9日,不代表本人现在的观点与看法。原始地址:http://blog.sina.com.cn/s/blog_6022c4720102vxaq.html
1、前言
数学在讲解析几何,现在了解一下信息学中的计算几何也是极好的,和解析几何几乎是相通的。前面的内容比较简单,甚至自己看看就行都不值得写篇文章了,但是为了后面的内容作铺垫还是写写好了。
本章节从头到尾没有去看过别人的博文,基本上都是看的刘汝佳的《算法竞赛入门经典训练指南》,所以很多讲解是原创,有误敬请指出。几何问题背景知识多,内容杂乱,有些地方容易混淆,大家细看。
2、建模
开始做几何问题之前,必须先要将一些定义写好。我们都知道,向量是有方向,大小的量,而点是坐标系上的一个个点(词穷了= =。)但是,在信息学里面的平面坐标系中,向量和点的定义是一致的——只有x,y两个变量。因为一个点就相当于把向量的起点平移到坐标原点之后的终点坐标。下面就是他们的定义:
----------------------------------------------------------------------------------------------------
struct point
{
double x,y;
point(double x=0,double y=0):x(x),y(y) {} // 构造函数,方便代码编写
};
typedef point vector; //从程序实现上看,vector只是point的别名
----------------------------------------------------------------------------------------------------
3、符号
有了向量的表示,如何计算?这里要用到运算符重载,重载+、-、*、/、<、==。如何写数学里面都学了吧,我就不详说了。大家只要注意一下dcmp的作用。
----------------------------------------------------------------------------------------------------
vector operator + (vector a,vector b) { return vector(a.x+b.x,a.y+b.y); }
vector operator - (point a,point b) { return vector(a.x-b.x,a.y-b.y); }
vector operator * (vector a,double num) { return vector(a.x*num,a.y*num); }
vector operator / (vector a,double num) { return vector(a.x/num,a.y/num); }
bool operator < (point a,point b) { if (a.x!=b.x) return (a.x
const double eps=1e-10;
int dcmp(double x) { if (abs(x)<0)?-1:1; } // abs函数为绝对值
bool operator == (vector a,vector b) { return ( dcmp(a.x-b.x)==0 && dcmp(a.y-b.y)==0); }
----------------------------------------------------------------------------------------------------
dcmp函数的作用是什么?当两个值差距很小时,同样会返回相同,即返回0,用以避免精度问题带来的麻烦。
4、基本运算
1、点积(Dot)。向量a和b的点积等于两者长度的乘积乘上它们夹角的余弦。夹角为从a到b逆时针旋转的角。因此,当夹角大于90°时,点积为负。顺便写上如何求向量长度(Length)和夹角(Angle):
----------------------------------------------------------------------------------------------------
double Dot(vector a,vector b) { return a.x*b.x+a.y*b.y; }
double Length(vector a) { return sqrt(Dot(a,a)); }
double Angle(vector a,vector b) { return acos(Dot(a,b)/Length(a)/Length(b)); } // acos为反余弦,全称arccos
----------------------------------------------------------------------------------------------------
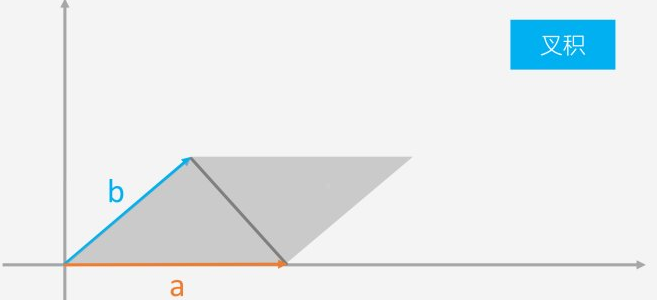
2、叉积(Cross)。数学里暂时没学,但是作用非常大!后面的面积都需要用到它,我开始看的时候还半天没看懂。两个向量a和b的叉积等于a和b组成的三角形的有向面积的两倍。有向面积的概念是,朝着向量a看,如果向量b在你左边,则叉积大于0;如果在你右边,则小于0。
 // 标准图已丢失
// 标准图已丢失如上图所示,Cross(a,b)>0,且它的值为灰色阴影部分的面积。
----------------------------------------------------------------------------------------------------
double Cross(vector a,vector b) { return a.x*b.y-a.y*b.x; } // 叉积
double Area2(point a,point b,point c) { return Cross(b-a,c-a); } // 由a,b,c三个点构成的平行四边形面积
----------------------------------------------------------------------------------------------------
根据上述的点积,叉积的公式以及作用,我们可以比较方便的得到两个向量的位置关系:

括号里第一个数是点积,第二个数是叉积。设向量a水平向右,根据向量a,b的点积叉积的正负零情况,可以得到向量b的大致方向。这在以后将有很大的作用。
5、直线
在数学里面,我们已经学了直线的多种表达方式——两点式,一般式等等,信息学里面采用参数式方程。任何一条直线可以用该直线上一点P0和方向向量v表示,则直线上所有点P满足P=P0+tv,t是一个参数。则直线的参数式为: P=P0+tv
1、直线交点(lineIntersection)。设两条直线分别为P+t1v和Q+t2w,设向量u=P-Q,则可以得到:
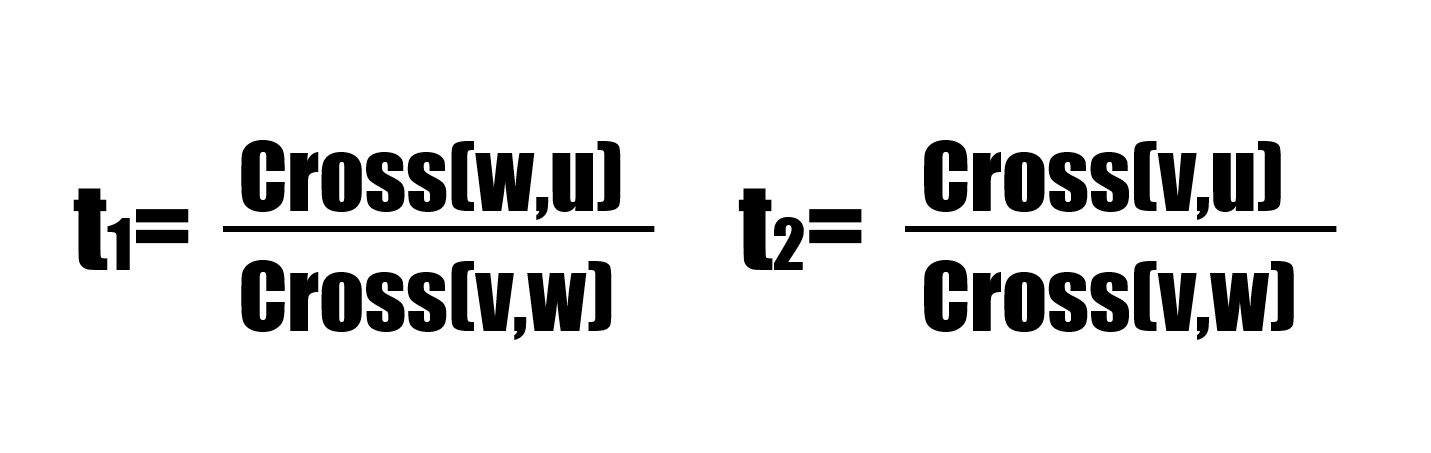
----------------------------------------------------------------------------------------------------
point lineIntersection(point p,vector v,point q,vector w)
{
vector u=p-q;
double t=Cross(w,u)/Cross(v,w);
return p+v*t;
}
----------------------------------------------------------------------------------------------------
2、点到直线的距离(Point to line)。很简单,直接用叉积即平行四边形的面积除以底边就可得到。
----------------------------------------------------------------------------------------------------
double Distance_PTL(point x,point a,point b)
{
vector v1=a-x,v2=b-x;
return (abs(Cross(v1,v2)/Length(v1)));
}
----------------------------------------------------------------------------------------------------
3、点到线段的距离(Point to segement)。注意是线段!也就是说,如果点到线段所在直线的垂线并不在线段上,那么点到线段的距离并不是直接和到直线的距离一样(很拗口,慢慢看)。设投影点为Q,如果在线段AB上,即为P到直线AB的距离;如果在射线BA上,则所求距离为PA;否则为PB。如何判断Q的位置?如下图:
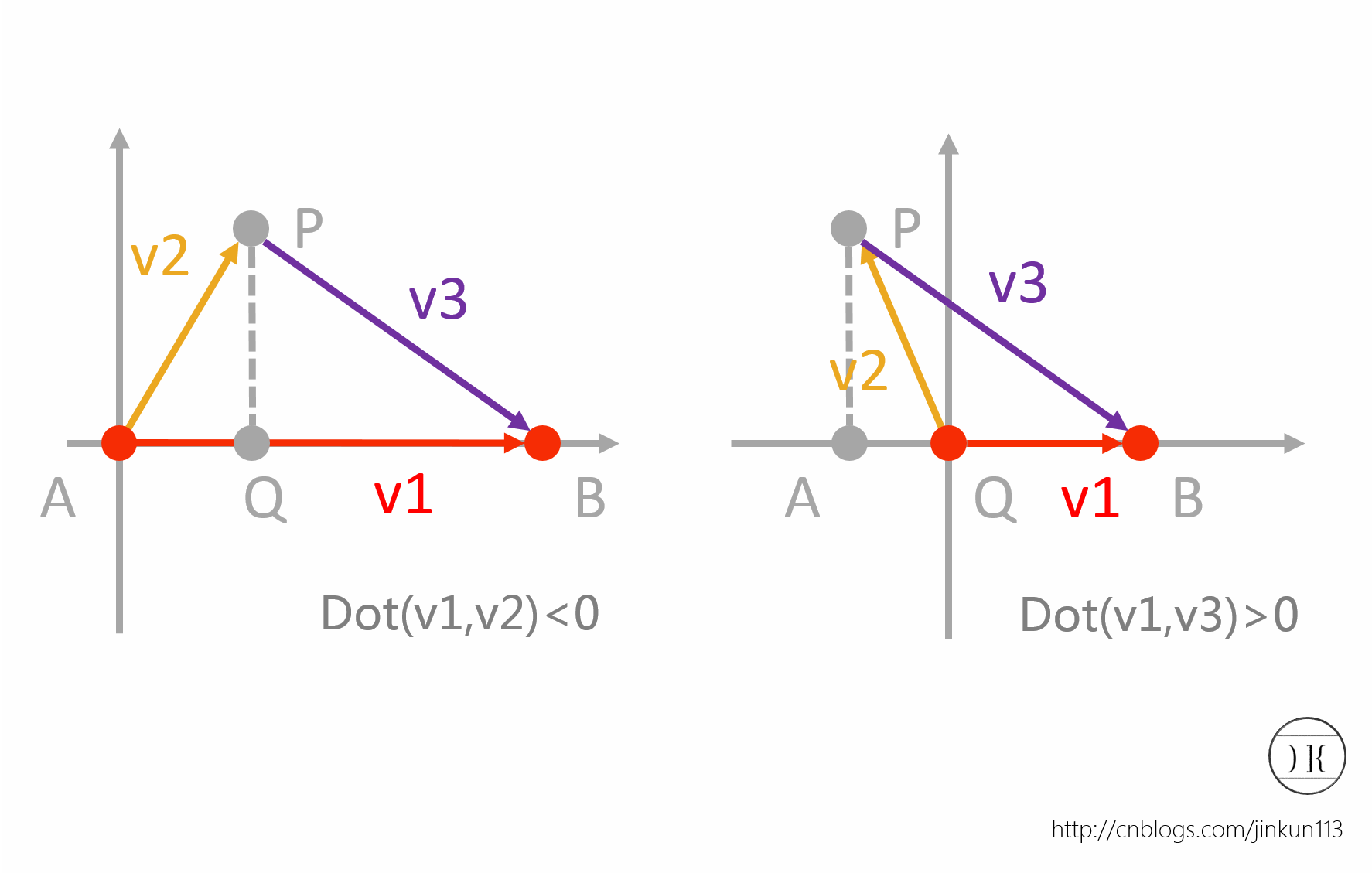
前面我们讲了利用点积叉积来判断两个向量的方向,这个地方就可以用到了。大家可以自己去试试v1,v2,v3之间的点积关系能够说明什么。
----------------------------------------------------------------------------------------------------
double Distance_PTS(point x,point a,point b)
{
if (a==b) return Length(x-a);
vector v1=b-a,v2=x-a,v3=x-b;
if (dcmp(Dot(v1,v2))<0) return Length(v2); // q在射线ba上
else if (dcmp(Dot(v1,v3))>0) return Length(v3); // q在射线ab上
else return fabs(Cross(v1,v2)/Length(v1)); // q在线段ab上
}
----------------------------------------------------------------------------------------------------
4、点在直线上的投影(lineProjection)。设AB的参数式为A+tv,P的投影点Q为Q=A+t0v,由于PQ⊥AB,则Dot(v,P-(A+t0v))=0,即Dot(v,P-A)-t0×Dot(v,v)=0,解出t0=Dot(v,x-a)/Dot(v,v),带入参数式,得Q点。
----------------------------------------------------------------------------------------------------
point lineProjection(point x,point a,point b)
{
vector v=b-a;
return (a+v*(Dot(v,x-a)/Dot(v,v)));
}
----------------------------------------------------------------------------------------------------
5、判断线段相交(Point to line)。判断条件:线段a的两个端点在线段b的两侧(即叉积符号不同)。
----------------------------------------------------------------------------------------------------
bool segmentIntersection(point a1,point a2,point b1,point b2)
{
double c1=Cross(a2-a1,b1-a1),c2=Cross(a2-a1,b2-a1),c3=Cross(b2-b1,a1-b1),c4=Cross(b2-b1,a2-b1);
return (dcmp(c1)*dcmp(c2)<0 && dcmp(c3)*dcmp(c4)<0);
}
----------------------------------------------------------------------------------------------------
6、多边形面积
将前面的知识全部铺垫好了,求多边形面积可以算是实战演练的第一步。求面积很简单,任取多边形的一个顶点(一般取读入的第一个顶点),从该点出发将多边形分成n-2个三角形,然后将面积加起来。

对于凸多边形来说,似乎比较好理解,如上图,S=S1+S2+S3+S4。凹多边形连接了每个顶点之后,可能会出现重叠面积和多边形以外的面积啊?可以确定的一点是,重叠面积=以外的面积(原因可以问你们数学老师)。所以无需顾虑,同样地,S=S1+S2+S3。
----------------------------------------------------------------------------------------------------
double polygonArea(point p[100],int n)
{
double area=0;
for (int i=1;i<=n-2;i++)
area+=Cross(p[i]-p[0],p[i+1]-p[0]);
return area/2;
}
----------------------------------------------------------------------------------------------------
7、总结
比较早就开始看这一章,但是搞了很久,主要是内容太杂了,搞得有点心烦。当然今天只讲了一些最基础的东西,后面将持续更新。
计算几何II——二维几何之凸包
计算几何III——二维几何之半平面交
计算几何IV——圆与圆的计算
计算几何V——三维几何(这玩意儿前提是我能搞懂= =)