总目录 > 8 图论 > 8.3 最小生成树
前言
树与图的紧密联系通过这一部分的内容就很好诠释了!名为生成树,实为图上问题,可以理解为由一张图生成一棵树。
子目录列表
1、连通图与生成树
2、最小生成树
3、Kruskal 算法
4、Prim 算法
5、Boruvka 算法(施工中)
6、最小生成树的唯一性(施工中)
7、次小生成树(施工中)
8.3 最小生成树
1、连通图与生成树
在 8.1 图的简介与相关概念 中,已经介绍了连通性相关的各类概念。这里以无向图为例,对连通性问题进行展开。
一个有 n 个结点的无向连通图,其生成树包含图中的全部 n 个结点,但只有 n - 1 条边,使其刚好构成一棵无根树。在生成树上添加任意一条边,都会使得构成一个环,而不再是树。根据定义,一张图的生成树往往不止一棵,比如:

右图的 8 棵树均是左图的生成树。
当且仅当无向图为连通图时,遍历只需要从任一顶点出发即可遍历全图,而非连通图,遍历次数等于其连通分量的个数。
非连通图显然不存在生成树,而存在生成森林 —— 由若干棵生成树组成的森林,棵数等于连通分量个数。
2、最小生成树
概念:对于无向赋权连通图,其所有的生成树中边权之和最小的生成树称之为最小生成树(MST, Minimum Spanning Tree)。
比如在上图中,图 e 即为左图的最小生成树,其边权和为 14。那么什么情况下需要这样的最小生成树呢?
【SCOI2005】【繁忙的都市】
城市 C 是一个非常繁忙的大都市,城市中的道路十分的拥挤,于是市长决定对其中的道路进行改造。城市 C 的道路是这样分布的:城市中有 n 个交叉路口,有些交叉路口之间有道路相连,两个交叉路口之间最多有一条道路相连接。这些道路是双向的,且把所有的交叉路口直接或间接的连接起来了。每条道路都有一个分值,分值越小表示这个道路越繁忙,越需要进行改造。但是市政府的资金有限,市长希望进行改造的道路越少越好,于是他提出下面的要求:
(1) 改造的那些道路能够把所有的交叉路口直接或间接的连通起来。
(2) 在满足要求 (1) 的情况下,改造的道路尽量少。
(3) 在满足要求 (1)、(2) 的情况下,改造的那些道路中分值最大的道路分值尽量小。
任务:作为市规划局的你,应当作出最佳的决策,选择那些道路应当被修建。
题目说了一大通,本质就是对一张有 n 个点的无向赋权连通图求最小生成树。构造最小生成树有很多种方法,下面介绍最常用的 Kruskal 克鲁斯卡尔算法和 Prim 普利姆算法,以及 Boruvka 算法。
3、Kruskal 算法
① 思路
Kruskal 算法是图论问题中少有的需要使用边存储的方式存图的算法。
将所有边按照边权从小到大排序,初始默认图中没有任何边,每次取出当前边权最小的边,如果加上该边没有构成环,则加;如果构成环,则跳过这条边,直到加入 n - 1 条边,即形成了最小生成树。
② 证明
略。
③ 实现
根据思路,每次加边需要判断是否会构成环,即等价于该边的两个结点是否已经连通,等价于两个结点是否已经已经在同一棵树中,这个过程需要使用并查集(请参见:<施工中>)来维护即可。
使用 O(m log m) 的排序算法与 O(m log n) 的并查集,总时间复杂度为 O(m log m)。
④ 例题代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 305 5 #define MAXM 10005 6 7 int n, m, fa[MAXN], tot, ans; 8 9 class Edge { 10 public: 11 int u, v, w; 12 bool operator < (const Edge &o) const { 13 return w < o.w; 14 } 15 } e[MAXM]; 16 17 int find(int o) { 18 return o == fa[o] ? o : fa[o] = find(fa[o]); 19 } 20 21 int main() { 22 cin >> n >> m; 23 for (int i = 1; i <= m; i++) 24 cin >> e[i].u >> e[i].v >> e[i].w; 25 sort(e + 1, e + m + 1); 26 for (int i = 1; i <= n; i++) fa[i] = i; 27 for (int i = 1; i <= m; i++) { 28 int x = find(e[i].u), y = find(e[i].v); 29 if (x == y) continue; 30 else { 31 fa[x] = y; 32 tot++, ans = e[i].w; 33 if (tot == n - 1) break; 34 } 35 } 36 cout << n - 1 << ' ' << ans; 37 return 0; 38 }
(例题本身就是个纯最小生成树模板题)
4、Prim 算法
① 思路
初始默认图中只有任意一个结点,将结点分为两个集合:已加入的,未加入的,初始只有一个结点在已加入集合中。每次从未加入的结点中,找到一个与已加入的结点之间边权最小值最小的结点,将其加入到图中,并连上这条边权最小的边,直到加入了 n - 2 个结点,即形成了最小生成树。
② 证明
略。
③ 实现
根据思路,每次加点需要找到边权最小的边,可以暴力找也可以使用堆维护。
暴力的话总时间复杂度为 O(n ^ 2 + m),使用二叉堆为 O((n + m) log n),使用斐波那契堆为 O(n log n + m)。
④ 例题代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 305 5 #define MAXM 10005 6 7 int n, m, u, v, w, o, h[MAXN], tot, vis[MAXN], ans; 8 9 class Edge { 10 public: 11 int v, nxt, w; 12 bool operator < (const Edge &o) const { 13 return w > o.w; 14 } 15 } e[MAXM << 1]; 16 17 priority_queue <Edge> Q; 18 19 void add(int u, int v, int w) { 20 o++, e[o] = (Edge) {v, h[u], w}, h[u] = o; 21 } 22 23 int main() { 24 cin >> n >> m; 25 for (int i = 1; i <= m; i++) { 26 cin >> u >> v >> w; 27 add(u, v, w), add(v, u, w); 28 } 29 vis[1] = 1; 30 for (int x = h[1]; x; x = e[x].nxt) 31 Q.push(e[x]); 32 while (tot < n - 1) { 33 Edge o = Q.top(); Q.pop(); 34 if (vis[o.v]) continue; 35 tot++, vis[o.v] = 1, ans = max(ans, o.w); 36 for (int x = h[o.v]; x; x = e[x].nxt) 37 Q.push(e[x]); 38 } 39 cout << n - 1 << ' ' << ans; 40 return 0; 41 }
5、Boruvka 算法
暂略。
6、最小生成树的唯一性
最小生成树显然不一定是唯一的。 比如下图 a 和 b 两个生成树:
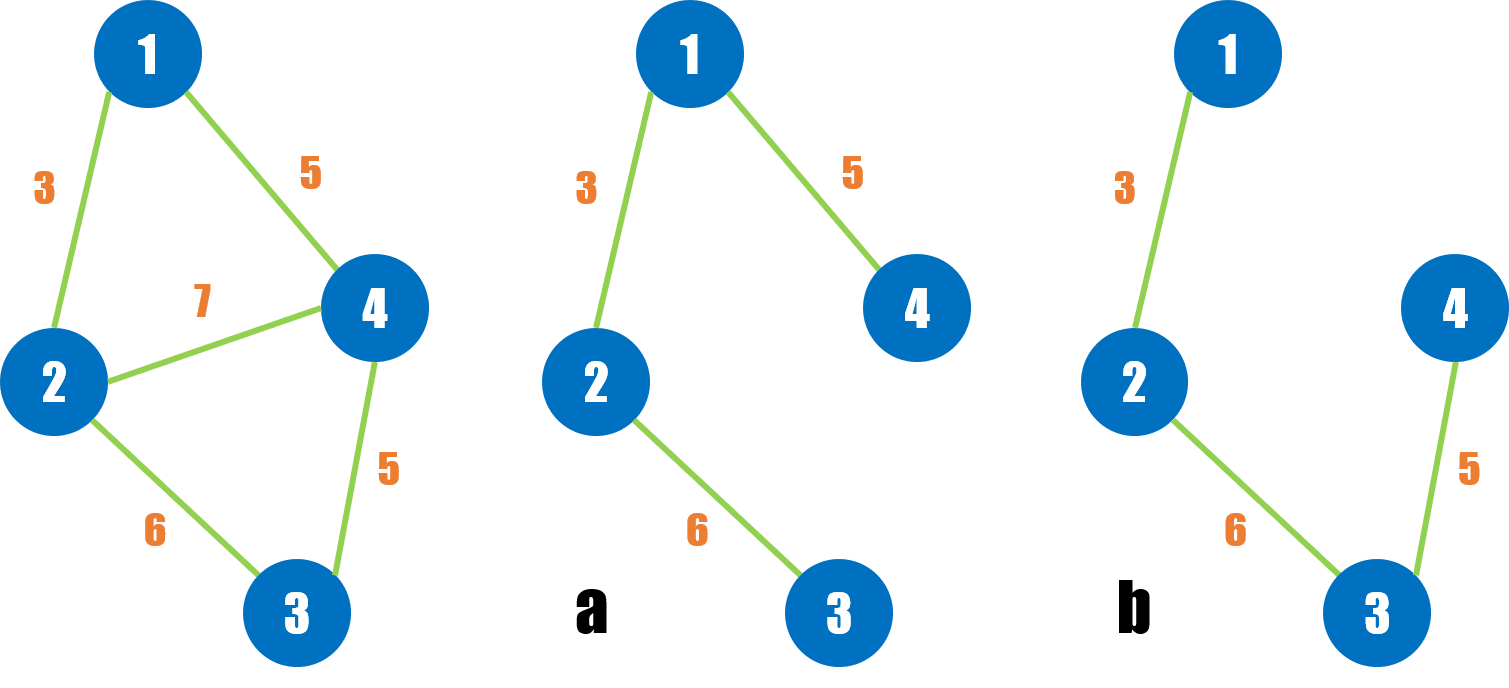
更多分析暂略。
7、次小生成树
暂略。