线性同余方法(LCG)是个产生伪随机数的方法。
它是根据递归公式:
其中 是产生器设定的常数。
是产生器设定的常数。
LCG的周期最大为 ,但大部分情况都会少于M。要令LCG达到最大周期,应符合以下条件:
,但大部分情况都会少于M。要令LCG达到最大周期,应符合以下条件:
线性同余算法有m 、a 、c 和X0 4个参数,通过置Xn + 1 ≡aXn + c (mod m) ,求得随机数序列< Xn > , 这个序列称作线性同余序列。m、a 、c 和X0 分别称做模数、乘数、增量和初始值。线性同余方法速度快,如果对乘数和模数进行适当的选择,可以满足用于评价一个随机数产生器的3 种准则:
1.这个函数应该是一个完整周期的产生函数。也就是说,这个函数应该在重复之前产生出0 到m之间的所有数;
2.产生的序列应该看起来是随机的;
3.这个函数应该用32bit 算术高效实现。
在我的算法中,a=7^5;c=0;m=2^31-1; x0为系统时间;
我的代码如下:
- #include <stdio.h>
- #include <time.h>
- static unsigned long rand_seed;
- void mysrand (unsigned long int);
- void myrand ();
- int
- main (void)
- {
- int i;
- mysrand (time (NULL));
- for (i = 0; i < 100; i++)
- {
- myrand ();
- }
- return 0;
- }
- void
- mysrand (unsigned long seed)
- {
- rand_seed = seed;
- }
- void
- myrand ()
- {
- rand_seed = (rand_seed * 16807L) % ((1 << 31) - 1);
- printf ("%ld ", rand_seed);
- }
===============PS==================
产生随机种子的方法很多,目前用得比较多的是使用系统时间为种子。我觉得这种方法也不妥当。假如我批量执行程序,程序执行的时间是几个ms,那么几个相邻程序的种子就是一样的,产生的结果因此也是一样的。(因为系统时间是按照秒来计算的,一秒内执行多少次,产生的随机种子就有多少相同的。)
比较流行的是使用seed = (seed * 9301 + 49297) % 233280;
return seed / (233280.0);
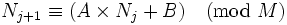
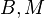
 ;
;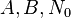 都比
都比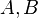 是正整数。
是正整数。