以下摘自AC大神的。据说百度空间要关了,所以,备份一下。。。
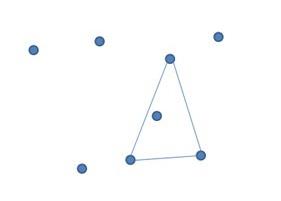

现在我们定义:
s(i,j) 表示 (i -> j)的 “右边”的点的个数
g(i,j,k) 表示以 i为中心,从j点到k点的这个角度区间内部有多少个点。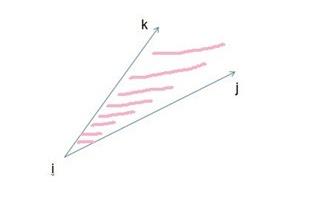
假设 i->j->k 已经按照逆时针的顺序
那么观察g(i, j, k) + g(j, k, i)+ g(k, i, j)+ s[i][j] + s[j][k] + s[k][i];
发现了规律 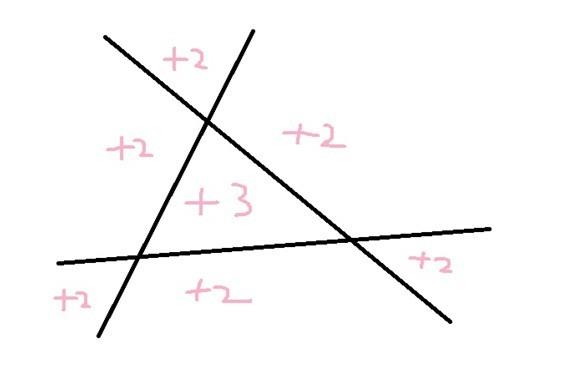
其中 +2, + 3表示这个区域被算了几次
于是我们可以知道
Ans = g(i, j, k) + g(j, k, i)+ g(k, i, j)+ s[i][j] + s[j][k] + s[k][i] - 2 * (n – 2);
O(1)
如何求s(i,j), g(i,j,k)
(1) 枚举点,并把其他点按照与当前点的极角排序
可以知道,由于不存在3点共线,于是每一个极角最多只可能存在1个点,并有极角差为180度的2个极角至多只有1个点。(否则3点共线,矛盾)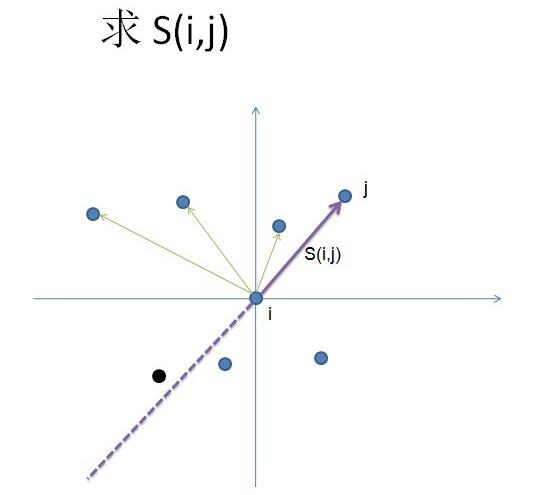
容易发现(i, j) “左边”的点数是很容易得到的,只需要二分得到黑色点的位置,之后统计个数即可!
于是(i,j) 右边的也可以得到,只需要把总的 (n - 2)个点减去左边的即可 //我认为这里应该是n-3个点才对。
在这一步,我们用O(n * n logn)的时间求得了 S(i,j)
g(i,j,k) 的思路完全类似,复杂度也为 O(n ^2 logn)
所以本题的复杂度为 O(n^2 logn + M)
这种解法很巧妙了,极角排序是运用得最巧妙的地方。排序后通过二分求得一边的点数,确实利害。
HDU 4380
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#define LL __int64
using namespace std;
#define pi acos(-1.0)
struct Node{
double x,y;
}Nv[105],Mv[1005];
int n,m;
double ang[1005], Ntang[105][105];
int s[105][105],Right[105][105];
int binsearch(double ave){
int l=1,r=m;
int ans=0;
while(l<=r){
int mid=(l+r)/2;
if(ang[mid]<ave){
ans=mid,l=mid+1;
}
else r=mid-1;
}
return ans;
}
void initial(){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(i==j) continue;
Ntang[i][j]=atan2(Nv[j].y-Nv[i].y,Nv[j].x-Nv[i].x);
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
ang[j]=atan2(Mv[j].y-Nv[i].y,Mv[j].x-Nv[i].x);
}
sort(ang+1,ang+1+m);
for(int j=1;j<=n;j++){
if(j==i) continue;
double tmp=Ntang[i][j];
int pos1=binsearch(tmp);
s[i][j]=pos1; //s表示极角小于tmp的个数。因为没有三点共线,所以小于。记录下这个值使得求直线一边的点数很方便
if(tmp>0){
tmp=tmp-pi;
int pos2=binsearch(tmp);
Right[i][j]=pos1-pos2;
}
else{
tmp=tmp+pi;
int pos2=binsearch(tmp);
Right[i][j]=m-(pos2-pos1);
}
}
}
}
int Get(int i,int j,int k){
double ang1=Ntang[j][i];
double ang2=Ntang[j][k];
if(ang1>ang2){
if(ang1-ang2<pi) return s[j][i]-s[j][k];
else return m-(s[j][i]-s[j][k]);
}
else{
if(ang2-ang1<pi) return s[j][k]-s[j][i];
else return m-(s[j][k]-s[j][i]);
}
}
int main(){
int icase=0;
while(scanf("%d%d",&n,&m)!=EOF){
for(int i=1;i<=n;i++){
scanf("%lf%lf",&Nv[i].x,&Nv[i].y);
}
for(int j=1;j<=m;j++){
scanf("%lf%lf",&Mv[j].x,&Mv[j].y);
}
initial();
int ans=0;
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
for(int k=j+1;k<=n;k++){
int tmp=Get(i,j,k)+Get(j,k,i)+Get(k,i,j)+Right[i][j]+Right[j][k]+Right[k][i]-2*m;
if(tmp&1) ans++;
}
}
}
printf("Case %d: %d
",++icase,ans);
}
return 0;
}
HDU 4367
此处注意数列是从0开始的。具体思路是:选定i,j两点连成一条直线,然后选择直线左边的的点k,通过连线ki,kj得到一个角。那么,这个角内的直线右边的点与K连线必定是与ij相交的。右边的点是角内的点减去三角形内的点。
此处应使用降幂公式:A^X=A^(X%PHI(C)+PHI(C))modC。其中(A,C)=1,是中C是素数,所以PHI(C)=C-1.
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cmath>
#define pi acos(-1.0)
#define LL __int64
using namespace std;
const LL MOD= 1000000007ll;
struct Node{
double x,y;
}Point[205];
double ang[205],Pang[205][205];
int Right[205][205],s[205][205];
int n;
LL fib[40005];
void predo(){
fib[0]=1;
fib[1]=1;
for(int i=2;i<40005;i++){
fib[i]=(fib[i-1]+fib[i-2])%(MOD-1ll)+(MOD-1ll);
}
}
int binsearch(double ag){
int l=1,r=n-1;
int ret=0;
while(l<=r){
int m=(l+r)/2;
if(ang[m]<ag){
ret=m;
l=m+1;
}
else r=m-1;
}
return ret;
}
void initial(){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(i==j) continue;
Pang[i][j]=atan2(Point[j].y-Point[i].y,Point[j].x-Point[i].x);
}
}
int nt;
for(int i=1;i<=n;i++){
nt=0;
for(int j=1;j<=n;j++){
if(i==j) continue;
ang[++nt]=atan2(Point[j].y-Point[i].y,Point[j].x-Point[i].x);
}
sort(ang+1,ang+1+nt);
for(int j=1;j<=n;j++){
if(i==j) continue;
double tmp=Pang[i][j];
int pos1=binsearch(tmp);
s[i][j]=pos1;
if(tmp>=0){
tmp-=pi;
int pos2=binsearch(tmp);
Right[i][j]=pos1-pos2;
}
else{
tmp+=pi;
int pos2=binsearch(tmp);
Right[i][j]=n-1-(pos2-pos1);
}
}
}
}
int getS(int i,int j,int k){
double ang1=Pang[j][i];
double ang2=Pang[j][k];
if(ang1>ang2){
if(ang1-ang2<pi) return s[j][i]-s[j][k]-1;
else{
return n-3-(s[j][i]-s[j][k]-1);
}
}
else{
if(ang2-ang1<pi) return s[j][k]-s[j][i]-1;
else return n-3-(s[j][k]-s[j][i]-1);
}
}
LL quick(LL num,LL p){
LL ret=1ll;
while(p){
if(p&1ll) ret=(ret*num)%MOD;
num=(num*num)%MOD;
p>>=1ll;
}
return ret;
}
int main(){
predo();
while(scanf("%d",&n)!=EOF){
for(int i=1;i<=n;i++)
scanf("%lf%lf",&Point[i].x,&Point[i].y);
initial();
/* for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++)
cout<<s[i][j]<<" ";
cout<<endl;
}*/
LL ans=1ll; LL num;
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
num=0;
// chi=i,chj=j;
for(int k=1;k<=n;k++){
if(k==i||k==j) continue;
if((Point[i].x-Point[k].x)*(Point[j].y-Point[k].y)-(Point[j].x-Point[k].x)*(Point[i].y-Point[k].y)<0) continue;
int tmp=getS(i,j,k)+getS(j,k,i)+getS(k,i,j)+Right[i][j]+Right[j][k]+Right[k][i]-2*(n-3);
tmp=getS(j,k,i)-tmp;
// cout<<i<<" "<<k<<" "<<j<<" ="<<tmp<<endl;
num+=(LL)tmp;
}
// cout<<num<<endl;
ans=(ans*(quick(num,fib[num])+1ll)%MOD)%MOD;
// cout<<ans<<endl;
}
}
printf("%I64d
",ans);
}
return 0;
}