第二章 插值法
1、拉格朗日基函数,可从线性插值基函数开始构造,简写过程如下:

2、牛顿基函数为{1,(x-x0),(x-x0)(x-x1),…,(x-x0)(x-x1)…(x-xn)},牛顿插值基函数中带有常数项x0,x1,…,xn,这与单项式基不同。
3、形如f[x0,x1,…,xn]=(f[x0,x1,…,xn-2,xn]-f[x0,x1,…,xn-2,xn-1])/(xn-xn-1),称为f(x)的k阶均差,具有以下的基本性质:
(1)均差与节点的排列次序无关,即均差具有对称性(拉格朗日插值函数的应用)k阶均差可以表示为函数值f(x0),f(x1),…,f(xn)的线性组合,即f[x0,x1,…,xk]=∑kj=0(f(xj)/(xj-x0)…(xj-xj-1)(xj-xj+1)…(xj-xk))。
(2)由性质1和k阶均差的性质f[x0,x1,…,xn]=(f[x0,x1,…,xk]-f[x0,x1,…,xk-1])/(xk-x0)(分子前项多xk)。
(3)若f(x)在[a,b]上存在n解导数,且节点x0,x1,…,xn-2,xn属于[a,b],则n阶均差与导数的关系为f[x0,x1,…,xn]=fn+1(ζ)/n!。
4、n+1个点的拉格朗日插值多项式和牛顿插值多项式的异同:

5、(1)单项式基底为{1,x,x2,…,xn},已知数为{x0,x1,…,xn},则未知数为{a0,a1,…,an}则系数矩阵为(不存在0元素,全为非零元素)
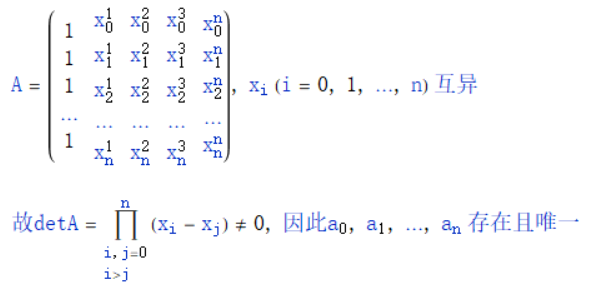
(2)拉格朗日基底为{l0(x),l1(x),…,ln(x)},已知数为{y0,y1,…,yn},未知数为{l0(x),l1(x),…,ln(x)}。
(3)牛顿的基底为{1,(x-x0),(x-x0)(x-x1),…,(x-x0)(x-x1)…(x-xn)},已知数为{x0,x1,…,xn},未知数为{a0,a1,…,an},则系数矩阵为

6、按照工作量,排序如下:牛顿插值、拉格朗日插值、多项式插值。
7、给出插值多项式余项,估计阶段误差

8、埃尔米特插值最显著的特征是:即要求节点上的函数值相等,同时也要求节点上到数值相等,甚至高阶导数值相等。泰勒公式:
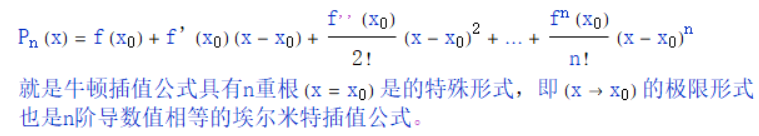
9、根据龙格函数(Ronge)发现的现象,发现高次多项式插值Ln(x)近似f(x)的效果并不好。产生的主要原因是计算时的舍入误差引起。
10、三次埃尔米特插值要求给出节点上的函数值和导数值,只有一阶导数连续。三次样条插值要求给出各节点的函数孩子和区间的边界值,具有二阶导数连续。从上可以看书,三次样条插值更优越,对节点的要求较低,具有二阶导数连续(插值函数更光滑)。
11、(1)✖,因为插值函数唯一。
(2)✔。
(3)✔,因为余项等于0.
(4)✖,典型的例子是龙格现象。
(5)✔,n越大说明步长h→0,此时S(x),S'(x),和S''(x)均一致检验与f(x),f'(x)和f''(x)。
(6)✖,典型的例子是龙格现象。
(7)✔。