一个函数调用其它函数好理解,但一个函数调用自身函数(这就是递归),代码看起来就不好懂了,容易把人绕进去出不来。不就是一个函数吗,为什么会让人看不懂呢?因为理解递归应该从整体(即整个函数体是否能解决问题)来看,而不是纠结于递归函数执行到了哪里!这是我研究了一遍又一遍最简单的递归代码得出得结论。我曾把二叉树的前序遍历(递归形式)的每一步代码都写出来,用python写的,因为python每次调用函数就缩进,能直观看出执行到哪了,结果发现递归确实能遍历,而且是按照可以从二叉树图形的每个结点顺序,其实也是,代码的执行不就是遍历了每个结点吗?要是代码没有按照设想的逻辑运行,那这个函数不就没实现功能,就是错的代码吗?
递归问题具体表现就是在函数中调用自身函数,每次调用问题的规模都变小了,直到遇到base case,一层层返回(可能是直接调用return,也可能函数体执行完返回的)问题就解决了,因此递归问题必须可以分解为若干个规模较小、与原问题形式相同的子问题,这些子问题可以用相同的解题思路来解决,这样才能从开始传一个参数,然后执行过程中不断调用自身函数直到最后得到问题的解。
拿斐波那契问题的代码来分析:
long long Fib(int n)
{
if(n <= 0)
return 0;
if(n == 1)
return 1;
return Fib(n-1)+Fib(n-2);
}
由斐波那契数列的递归代码可知,每个数都是f(n-1)+f(n-2),其base case是当n=0是f(n)=0,当n=1时,f(n)=1。函数也确实就是这样实现的,那为什么新手阅读代码还会理解不了?当看到return Fib(n-1)+Fib(n-2)时,新手会去想Fib(n-1)和Fib(n-2)的计算过程,多重复这个过程几遍就把自己绕进去了,不知道计算到Fib()哪个。如下图所示,求n=10的斐波那契数列,n=10作为参数传进函数,递归后就需计算n=9和n=8;而n=9递归后计算n=8和n=7,n=8递归后计算n=7和n=6,n=9是n=8、7、6、5、4、3、2、1计算来的,n=8是n=7、6、5、4、3、2、1计算来的,是分别单独递归计算得到,用递归的树型结构可直观看出,数的每个结点都计算了,怎么计算来的,由更底下的结点推算而来到最底下的结点即叶子,不是f(0)就是f(1)。
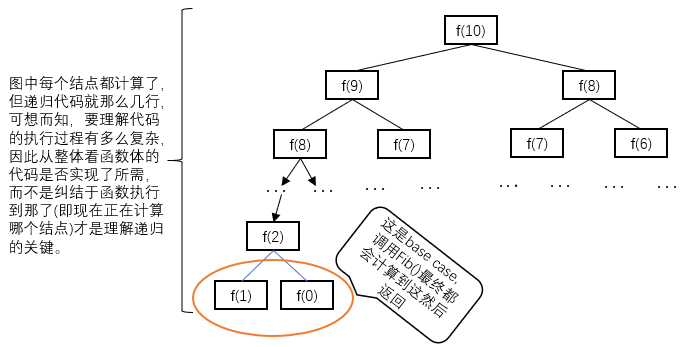
根据斐波那契数列,我们可以提取出递归的3要素:
1)、明确递归终止条件;
2)、给出递归终止时的处理办法;
3)、提取重复的逻辑,缩小问题规模。
再举一个例子:青蛙跳台阶问题。一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个n级的台阶总共有多少种跳法。
只有1级台阶时,只有1种跳法,即跳上1级台阶;
有2级台阶时,有2种跳法,连续2次跳1级台阶,或者直接跳上2级台阶;
有3级台阶时,有3种跳法:第一种是直接连续跳3次1级台阶,第二种是先跳1级再跳2级,第三种是先跳2级,再跳1级;
有4级台阶时,有5种跳法;
有5级台阶时,有8种跳法;
…
3=2+1,5=3+2,8=5+3…
直觉好的人已经归纳出数学计算公式:f(n)=f(n-1)+f(n-2)。
另一个思考角度:把n级台阶的跳法看成n的函数,记为f(n)。我们从后往前看,首先考虑n级台阶,只能由第n-1级台阶跳1级上来,或是由第n-2级台阶跳2级; n-1级台阶时,只能由第n-2级跳1级上来,或由n-3级跳2级;
n-2级台阶时,只能由第n-3级跳1级上来,或由n-4级跳2级;
…
2级台阶时,只能由第1级跳1级上来,或由0级跳2级;
1级台阶时,只能由第0级跳1级上来;
就可以归纳得出:
这不就是斐波那契数列问题吗?
至于为什么可以把n级台阶的跳法看成f(n),第n级的跳法是由n-1级的跳法加上n-2级的跳法,一次类推。因为一种从0级跳到终点的路径就是一种跳法,如果画出树形结构,就能看到一条条从叶结点到根的路径,每一条路径都是一种跳法,即有多少叶结点就有多少种跳法,这就是为什么跳法可以用f(n)表示的原因。