作者:Vamei 出处:http://www.cnblogs.com/vamei
树的特征和定义
树(Tree)是元素的集合。我们先以比较直观的方式介绍树。下面的数据结构是一个树:
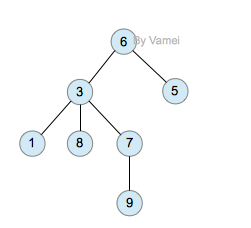
树有多个节点(node),用以储存元素。某些节点之间存在一定的关系,用连线表示,连线称为边(edge)。边的上端节点称为父节点,下端称为子节点。树像是一个不断分叉的树根。
每个节点可以有多个子节点(children),而该节点是相应子节点的父节点(parent)。比如说,3,5是6的子节点,6是3,5的父节点;1,8,7是3的子节点, 3是1,8,7的父节点。树有一个没有父节点的节点,称为根节点(root),如图中的6。没有子节点的节点称为叶节点(leaf),比如图中的1,8,9,5节点。从图中还可以看到,上面的树总共有4个层次,6位于第一层,9位于第四层。树中节点的最大层次被称为深度。也就是说,该树的深度(depth)为4。
如果我们从节点3开始向下看,而忽略其它部分。那么我们看到的是一个以节点3为根节点的树:
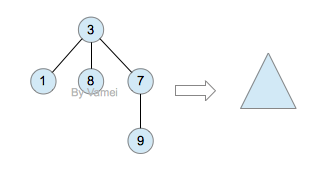
三角形代表一棵树
再进一步,如果我们定义孤立的一个节点也是一棵树的话,原来的树就可以表示为根节点和子树(subtree)的关系:
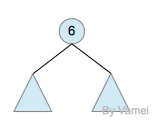
上述观察实际上给了我们一种严格的定义树的方法:
1. 树是元素的集合。
2. 该集合可以为空。这时树中没有元素,我们称树为空树 (empty tree)。
3. 如果该集合不为空,那么该集合有一个根节点,以及0个或者多个子树。根节点与它的子树的根节点用一个边(edge)相连。
上面的第三点是以递归的方式来定义树,也就是在定义树的过程中使用了树自身(子树)。由于树的递归特征,许多树相关的操作也可以方便的使用递归实现。我们将在后面看到。
(上述定义来自"Data Structures and Algorithm Analysis in C, by Mark Allen Weiss"。 我觉得有一点不太严格的地方。如果说空树属于树,第三点应该是 “...以及0个和多个非空子树...” )
树的实现
树的示意图已经给出了树的一种内存实现方式: 每个节点储存元素和多个指向子节点的指针。然而,子节点数目是不确定的。一个父节点可能有大量的子节点,而另一个父节点可能只有一个子节点,而树的增删节点操作会让子节点的数目发生进一步的变化。这种不确定性就可能带来大量的内存相关操作,并且容易造成内存的浪费。
一种经典的实现方式如下:
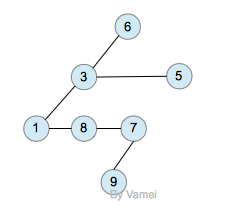
树的内存实现
拥有同一父节点的两个节点互为兄弟节点(sibling)。上图的实现方式中,每个节点包含有一个指针指向第一个子节点,并有另一个指针指向它的下一个兄弟节点。这样,我们就可以用统一的、确定的结构来表示每个节点。
计算机的文件系统是树的结构,比如Linux文件管理背景知识中所介绍的。在UNIX的文件系统中,每个文件(文件夹同样是一种文件),都可以看做是一个节点。非文件夹的文件被储存在叶节点。文件夹中有指向父节点和子节点的指针(在UNIX中,文件夹还包含一个指向自身的指针,这与我们上面见到的树有所区别)。在git中,也有类似的树状结构,用以表达整个文件系统的版本变化 (参考版本管理三国志)。
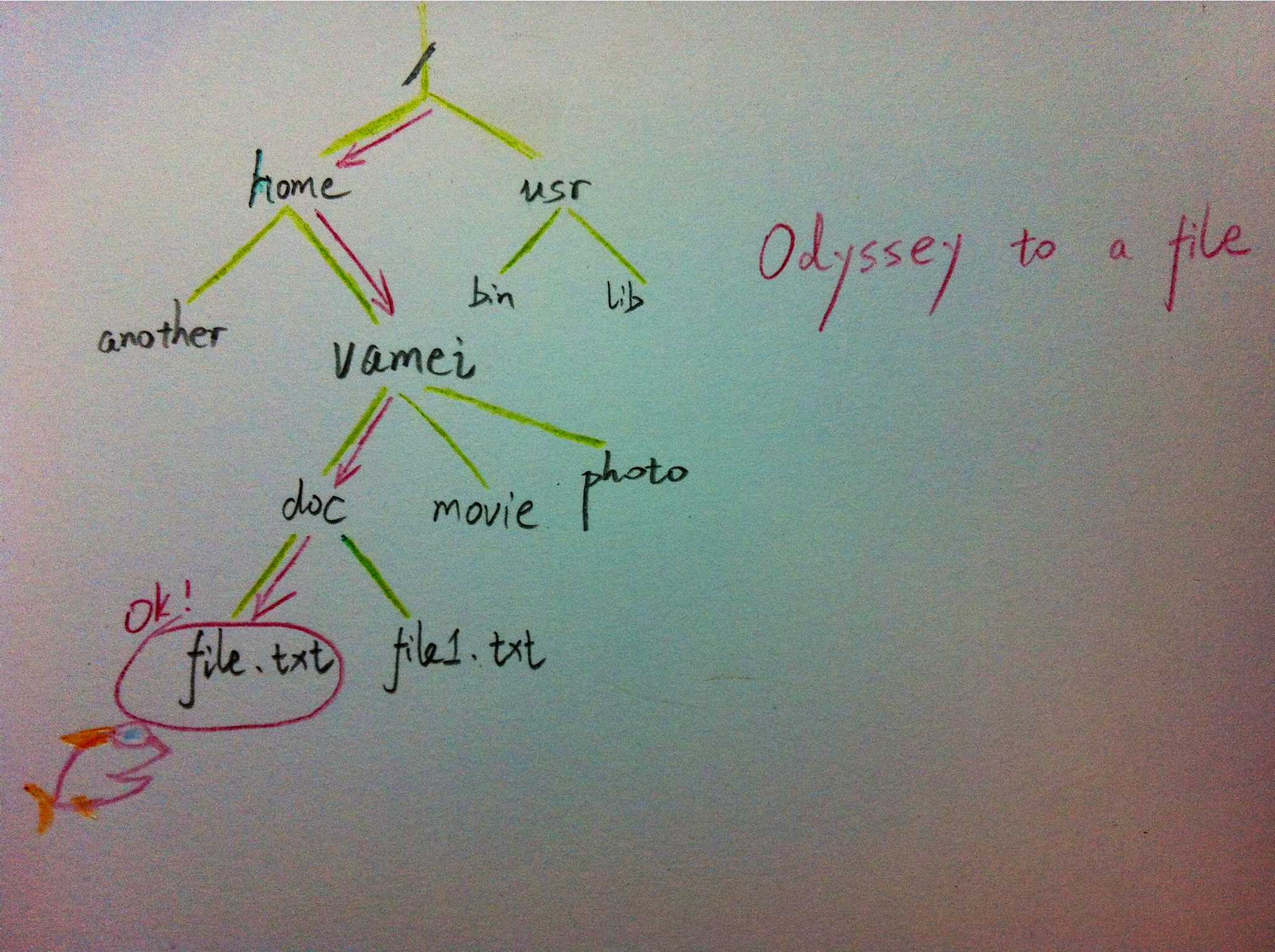
文件树
二叉搜索树的C实现
二叉树(binary)是一种特殊的树。二叉树的每个节点最多只能有2个子节点:
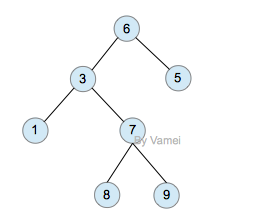
二叉树
由于二叉树的子节点数目确定,所以可以直接采用上图方式在内存中实现。每个节点有一个左子节点(left children)和右子节点(right children)。左子节点是左子树的根节点,右子节点是右子树的根节点。
如果我们给二叉树加一个额外的条件,就可以得到一种被称作二叉搜索树(binary search tree)的特殊二叉树。二叉搜索树要求:每个节点都不比它左子树的任意元素小,而且不比它的右子树的任意元素大。
(如果我们假设树中没有重复的元素,那么上述要求可以写成:每个节点比它左子树的任意节点大,而且比它右子树的任意节点小)
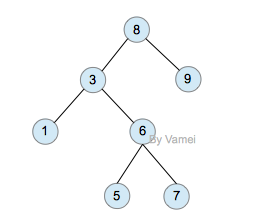
二叉搜索树,注意树中元素的大小
二叉搜索树可以方便的实现搜索算法。在搜索元素x的时候,我们可以将x和根节点比较:
1. 如果x等于根节点,那么找到x,停止搜索 (终止条件)
2. 如果x小于根节点,那么搜索左子树
3. 如果x大于根节点,那么搜索右子树
二叉搜索树所需要进行的操作次数最多与树的深度相等。n个节点的二叉搜索树的深度最多为n,最少为log(n)。
下面是用C语言实现的二叉搜索树,并有搜索,插入,删除,寻找最大最小节点的操作。每个节点中存有三个指针,一个指向父节点,一个指向左子节点,一个指向右子节点。
(这样的实现是为了方便。节点可以只保存有指向左右子节点的两个指针,并实现上述操作。)
删除节点相对比较复杂。删除节点后,有时需要进行一定的调整,以恢复二叉搜索树的性质(每个节点都不比它左子树的任意元素小,而且不比它的右子树的任意元素大)。
- 叶节点可以直接删除。
- 删除非叶节点时,比如下图中的节点8,我们可以删除左子树中最大的元素(或者右树中最大的元素),用删除的节点来补充元素8产生的空缺。但该元素可能也不是叶节点,所以它所产生的空缺需要其他元素补充…… 直到最后删除一个叶节点。上述过程可以递归实现。
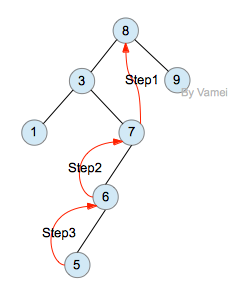
删除节点
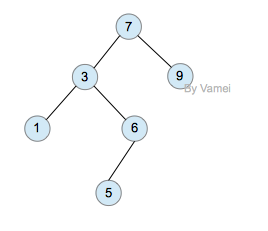
删除节点后的二叉搜索树
1 /* By Vamei */ 2 /* binary search tree */ 3 #include <stdio.h> 4 #include <stdlib.h> 5 6 typedef struct node *position; 7 typedef int ElementTP; 8 9 struct node { 10 position parent; 11 ElementTP element; 12 position lchild; 13 position rchild; 14 }; 15 16 /* pointer => root node of the tree */ 17 typedef struct node *TREE; 18 19 void print_sorted_tree(TREE); 20 position find_min(TREE); 21 position find_max(TREE); 22 position find_value(TREE, ElementTP); 23 position insert_value(TREE, ElementTP); 24 ElementTP delete_node(position); 25 26 static int is_root(position); 27 static int is_leaf(position); 28 static ElementTP delete_leaf(position); 29 static void insert_node_to_nonempty_tree(TREE, position); 30 31 void main(void) 32 { 33 TREE tr; 34 position np; 35 ElementTP element; 36 tr = NULL; 37 tr = insert_value(tr, 18); 38 tr = insert_value(tr, 5); 39 tr = insert_value(tr, 2); 40 tr = insert_value(tr, 8); 41 tr = insert_value(tr, 81); 42 tr = insert_value(tr, 101); 43 printf("Original: "); 44 print_sorted_tree(tr); 45 46 np = find_value(tr, 8); 47 if(np != NULL) { 48 delete_node(np); 49 printf("After deletion: "); 50 print_sorted_tree(tr); 51 } 52 } 53 54 55 /* 56 * print values of the tree in sorted order 57 */ 58 void print_sorted_tree(TREE tr) 59 { 60 if (tr == NULL) return; 61 print_sorted_tree(tr->lchild); 62 printf("%d ", tr->element); 63 print_sorted_tree(tr->rchild); 64 } 65 66 /* 67 * search for minimum value 68 * traverse lchild 69 */ 70 position find_min(TREE tr) 71 { 72 position np; 73 np = tr; 74 if (np == NULL) return NULL; 75 while(np->lchild != NULL) { 76 np = np->lchild; 77 } 78 return np; 79 } 80 81 /* 82 * search for maximum value 83 * traverse rchild 84 */ 85 position find_max(TREE tr) 86 { 87 position np; 88 np = tr; 89 if (np == NULL) return NULL; 90 while(np->rchild != NULL) { 91 np = np->rchild; 92 } 93 return np; 94 } 95 96 /* 97 * search for value 98 * 99 */ 100 position find_value(TREE tr, ElementTP value) 101 { 102 if (tr == NULL) return NULL; 103 104 if (tr->element == value) { 105 return tr; 106 } 107 else if (value < tr->element) { 108 return find_value(tr->lchild, value); 109 } 110 else { 111 return find_value(tr->rchild, value); 112 } 113 } 114 115 /* 116 * delete node np 117 */ 118 ElementTP delete_node(position np) 119 { 120 position replace; 121 ElementTP element; 122 if (is_leaf(np)) { 123 return delete_leaf(np); 124 } 125 else { 126 /* if a node is not a leaf, then we need to find a replacement */ 127 replace = (np->lchild != NULL) ? find_max(np->lchild) : find_min(np->rchild); 128 element = np->element; 129 np->element = delete_node(replace); 130 return element; 131 } 132 } 133 134 /* 135 * insert a value into the tree 136 * return root address of the tree 137 */ 138 position insert_value(TREE tr, ElementTP value) { 139 position np; 140 /* prepare the node */ 141 np = (position) malloc(sizeof(struct node)); 142 np->element = value; 143 np->parent = NULL; 144 np->lchild = NULL; 145 np->rchild = NULL; 146 147 if (tr == NULL) tr = np; 148 else { 149 insert_node_to_nonempty_tree(tr, np); 150 } 151 return tr; 152 } 153 154 155 //============================================= 156 157 /* 158 * np is root? 159 */ 160 static int is_root(position np) 161 { 162 return (np->parent == NULL); 163 } 164 165 /* 166 * np is leaf? 167 */ 168 static int is_leaf(position np) 169 { 170 return (np->lchild == NULL && np->rchild == NULL); 171 } 172 173 /* 174 * if an element is a leaf, 175 * then it could be removed with no side effect. 176 */ 177 static ElementTP delete_leaf(position np) 178 { 179 ElementTP element; 180 position parent; 181 element = np->element; 182 parent = np->parent; 183 if(!is_root(np)) { 184 if (parent->lchild == np) { 185 parent->lchild = NULL; 186 } 187 else { 188 parent->rchild = NULL; 189 } 190 } 191 free(np); 192 return element; 193 } 194 195 /* 196 * insert a node to a non-empty tree 197 * called by insert_value() 198 */ 199 static void insert_node_to_nonempty_tree(TREE tr, position np) 200 { 201 /* insert the node */ 202 if(np->element <= tr->element) { 203 if (tr->lchild == NULL) { 204 /* then tr->lchild is the proper place */ 205 tr->lchild = np; 206 np->parent = tr; 207 return; 208 } 209 else { 210 insert_node_to_nonempty_tree(tr->lchild, np); 211 } 212 } 213 else if(np->element > tr->element) { 214 if (tr->rchild == NULL) { 215 tr->rchild = np; 216 np->parent = tr; 217 return; 218 } 219 else { 220 insert_node_to_nonempty_tree(tr->rchild, np); 221 } 222 } 223 }
运行结果:
Original:
2
5
8
18
81
101
After deletion:
2
5
18
81
101
上述实现中的删除比较复杂。有一种简单的替代操作,称为懒惰删除(lazy deletion)。在懒惰删除时,我们并不真正从二叉搜索树中删除该节点,而是将该节点标记为“已删除”。这样,我们只用找到元素并标记,就可以完成删除元素了。如果有相同的元素重新插入,我们可以将该节点找到,并取消删除标记。
懒惰删除的实现比较简单,可以尝试一下。树所占据的内存空间不会因为删除节点而减小。懒惰节点实际上是用内存空间换取操作的简便性。
