目录
什么是支持向量机(SVM)
线性可分数据集的分类
线性可分数据集的分类(对偶形式)
线性近似可分数据集的分类
线性近似可分数据集的分类(对偶形式)
非线性数据集的分类
SMO算法
合页损失函数
Python代码(sklearn库)
|
什么是支持向量机(SVM) |
引例
假定有训练数据集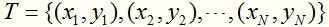 ,其中,x是向量,y=+1或-1。试学习一个SVM模型。
,其中,x是向量,y=+1或-1。试学习一个SVM模型。
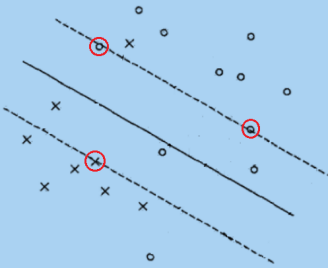
分析:将线性可分数据集区分开的超平面有无数个,但是SVM要做的是求解一个最优的超平面,最优意味着模型的泛化能力越强,具体做法就是选择使间隔最大的超平面。在图中可以看出黑色超平面优于红色超平面。红色圈内的样本就是支持向量,仅依靠支持向量就可以确定分割平面的位置。
李航《统计学习方法》中的定义
SVM是一种二类分类模型.它的基支持向量机(support vector machines,本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机; 支持向量机还包括核技巧,这使它成为实质上的非线性分类器。支持向量机的学习策略就是间隔最大化,可形式化为一个求解凸二次规划(convexquadratic programming) 的问题,也等价于正则化的合页损失函数的最小化问题.支持向量机的学习算法是求解凸二次规划的最优化算法。
|
线性可分数据集的分类 |
给定训练数据集 其中,x是向量,y=+1或-1。再假设训练数据集是线性可分的。试学习一个SVM模型。
其中,x是向量,y=+1或-1。再假设训练数据集是线性可分的。试学习一个SVM模型。
第一步:
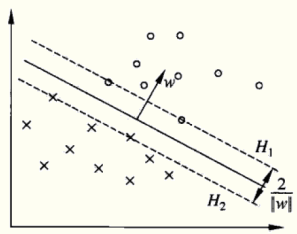
假设超平面为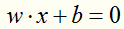
第二步:
构造并求解线性可分情况的最优化问题:

可转化成:
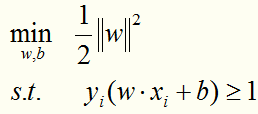
求解这个凸二次规划问题,可以得到唯一的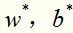
第三步:
得到分离超平面: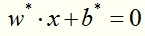
第四步:
得到分类决策函数: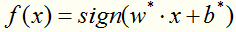
通过一个例子展示求解过程:(摘自李航《统计学习方法》)

|
线性可分数据集的分类(对偶形式) |
以上是求解原始形式的最优化问题,其实,还有一种对偶形式,使用对偶形式求解具有的优点是:
一、对偶形式更容易求解;
二、自然引入核函数,进而推广到非线性分类问题。
最优化问题转化到对偶形式的主要步骤是:构建拉格朗日函数然后求极值。
第一步:
假设超平面为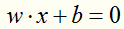
第二步:
将线性可分的最优化问题:
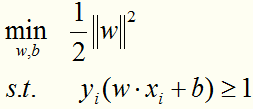
转化成线性可分的最优化问题的对偶形式:
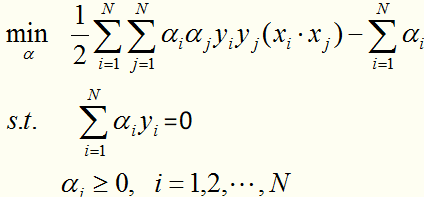
对于这种带约束求极值的问题,可以使用拉格朗日乘子法,可以求得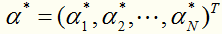 ,其中
,其中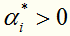 对应于训练集中的实例点就是支持向量。
对应于训练集中的实例点就是支持向量。
第三步:
得到分离超平面:
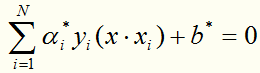
其中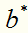 是唯一的,任取一个作为支持向量的实例点
是唯一的,任取一个作为支持向量的实例点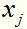 ,则可以算出
,则可以算出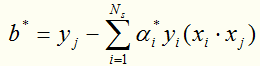
第四步:
得到分类决策函数:
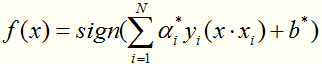
通过一个例子展示求解过程:(摘自李航《统计学习方法》)

|
线性近似可分数据集的分类 |
给定训练数据集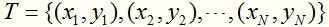 其中,x是向量,y=+1或-1。再假设训练数据集是线性近似可分的。试学习一个SVM模型。
其中,x是向量,y=+1或-1。再假设训练数据集是线性近似可分的。试学习一个SVM模型。
分析:线性近似可分意味着某些样本点不能满足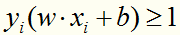 。
。
为了解决这个问题,可以对每个样本点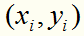 引进一个松弛变量
引进一个松弛变量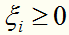 ,使所有样本点满足
,使所有样本点满足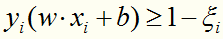
那么,如何求解这个间隔最大的超平面呢?
第一步:
假设超平面为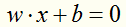
第二步:
将线性可分情况下的最优化问题:
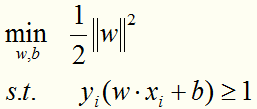
转化为线性近似可分情况下的最优化问题:
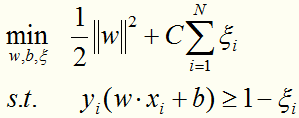
这个目标函数的含义:使间隔尽量大,同时使误分类的个数尽量小。C是一个惩罚参数,是调和二者的系数。C越大,分类器将力图通过分割超平面对所有的样例都正确分类。
求解这个凸二次规划问题,可以得到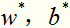 ,可以证明
,可以证明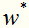 是唯一的,而
是唯一的,而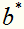 存在于一个区间。
存在于一个区间。
第三步:
得到分离超平面: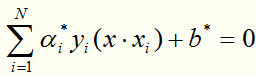
第四步:
得到分类决策函数: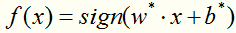
|
线性近似可分数据集的分类(对偶形式) |
第一步:
假设超平面为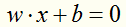
第二步:
将线性近似可分情况下的最优化问题:
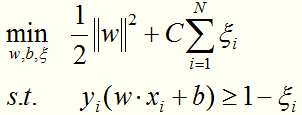
转化为线性近似可分情况下的最优化问题的对偶形式:
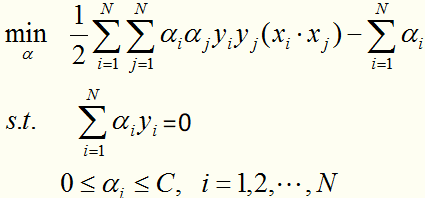
对于这种带约束求极值的问题,可以使用拉格朗日乘子法,可以求得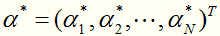 ,其中
,其中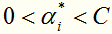 对应于训练集中的实例点就是落在间隔边界上的支持向量。
对应于训练集中的实例点就是落在间隔边界上的支持向量。
第三步:
得到分离超平面: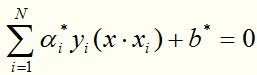
其中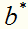 是不唯一的,一般求它的方法是:取每一个间隔边界上的支持向量实例点
是不唯一的,一般求它的方法是:取每一个间隔边界上的支持向量实例点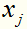 ,算出
,算出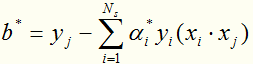 后取均值。
后取均值。
第四步:
得到分类决策函数: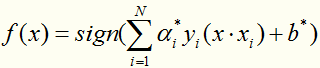
|
非线性数据集的分类 |
给定训练数据集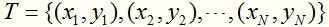 其中,x是向量,y=+1或-1。再假设训练数据集是非线性的。试学习一个SVM模型。
其中,x是向量,y=+1或-1。再假设训练数据集是非线性的。试学习一个SVM模型。
对于线性不可分的数据集,无法在原始空间上找到分离平面,所以要将原始数据映射到更高的维度,并找到一个间隔最大的超平面。




那么,如何求解这个间隔最大的超平面呢?
其实求解的关键就在于将数据映射到高维的空间,然后在高维的空间寻找最优分割超平面。
第一步:
假设超平面为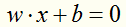
第二步:
将线性近似可分情况下的最优化问题的对偶形式:
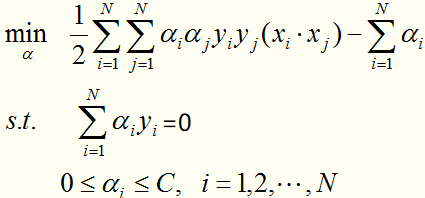
中的维度增加(将原始的维度空间映射到高维空间):

比如:在原始空间上样本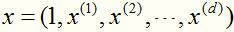 的特征是d+1维的,映射到高维空间 (d*d+1维)变成:
的特征是d+1维的,映射到高维空间 (d*d+1维)变成: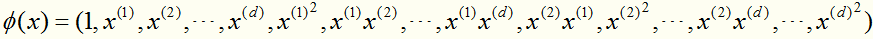 (思想:既然我在原始空间找不到超平面,不妨去高维空间寻找)
(思想:既然我在原始空间找不到超平面,不妨去高维空间寻找)
在高维空间使用线性支持向量机求间隔最大的分离超平面。这样做可以成功,但是计算复杂度会急增,因为增加了训练的难度。如何解决呢?
这里引入核函数,核函数的作用就是:通过一种“偷吃步”的技巧,让我们能够在高维空间求解,而且还能将计算复杂度降下来。下面看一下核函数是如何工作的。
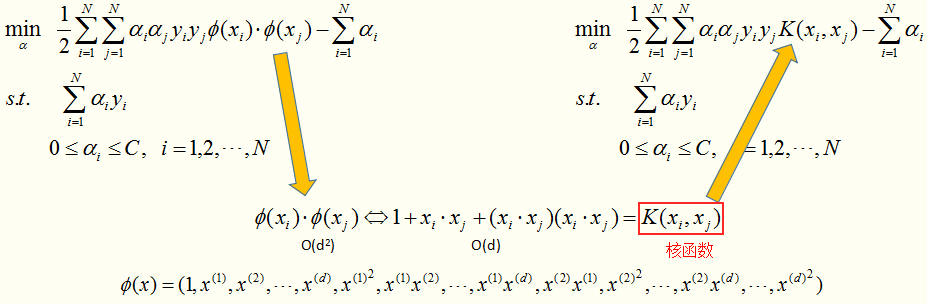
对于这种带约束求极值的问题,可以使用拉格朗日乘子法,可以求得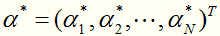 ,其中
,其中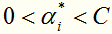 对应于训练集中的实例点就是落在间隔边界上的支持向量。
对应于训练集中的实例点就是落在间隔边界上的支持向量。
第三步:
得到分离超平面(求解过程与线性近似可分的情况相同,Ns是支持向量个数):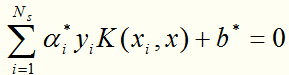
第四步:
得到分类决策函数:
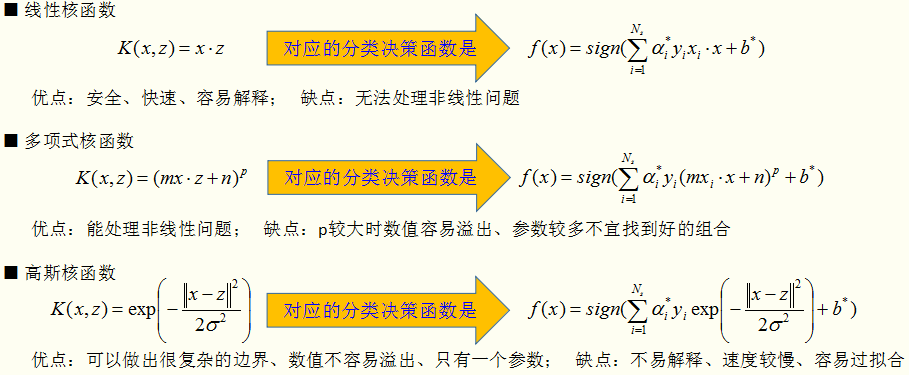
有了核函数,就无需人为的去定义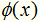 了,那么核函数的选择有哪些讲究呢? 其实,在实际应用中,往往依赖领域知识选择核函数,核函数的选择的有效性需要通过实验验证。 下面介绍常用的核函数,以及他们的优缺点。
了,那么核函数的选择有哪些讲究呢? 其实,在实际应用中,往往依赖领域知识选择核函数,核函数的选择的有效性需要通过实验验证。 下面介绍常用的核函数,以及他们的优缺点。
|
SMO算法 |
支持向量机的学习关键在于求解凸二次规划,这样的凸二次规划问题具有全局最优解。但是当训练样本很多时,需要一种高效的实现算法,SMO算法就是一种主流的高效的算法。 SMO算法要解决如下凸二次规划的对偶问题:

在这个问题里,变量是拉格朗日乘子,一个变量 对应一个样本点;变量的总数等于训练样本容量N。SMO的特点是不断地将原二次规划问题分解为只有两个变量的二次规划子问题,并对子问题进行解析求解,也就是每一步确定2个
对应一个样本点;变量的总数等于训练样本容量N。SMO的特点是不断地将原二次规划问题分解为只有两个变量的二次规划子问题,并对子问题进行解析求解,也就是每一步确定2个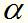 直到求完所有
直到求完所有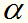 为止。子问题求解是快速的,即使有很多这样的子问题,SMO的求解也是高效的。
为止。子问题求解是快速的,即使有很多这样的子问题,SMO的求解也是高效的。
|
合页损失函数 |
对于线性支持向量机学习来说,其模型为分离超平面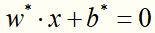 及决策函数
及决策函数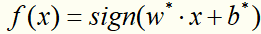 ,其学习策略为软间隔最大化,学习算法为凸二次规划。
,其学习策略为软间隔最大化,学习算法为凸二次规划。
线性支持向量机还有另一种解释,就是最小化以下目标函数:
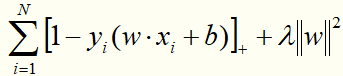
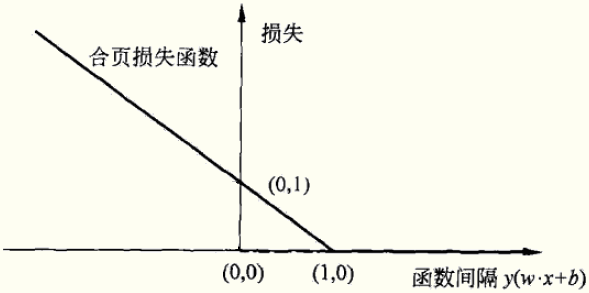
目标函数的第1项是经验损失,函数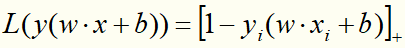 称为合页损失函数。下标“+”表示若值非正就为0;若为正就为其本身。这就是说,当样本点
称为合页损失函数。下标“+”表示若值非正就为0;若为正就为其本身。这就是说,当样本点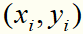 被正确分类且函数间隔(确定度)
被正确分类且函数间隔(确定度)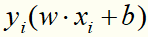 大于1时,损失是0,否则是
大于1时,损失是0,否则是 。
。
目标函数的第2项是系数为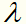 的
的 的L2范数,是正则化项,防止过拟合的。
的L2范数,是正则化项,防止过拟合的。
定理:线性支持向量机原始最优化问题:
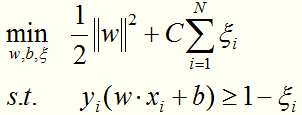
等价于最优化问题:
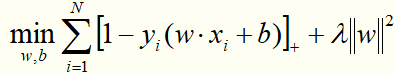
证明(摘自李航《统计学习方法》):

合页损失函数的图形为:
|
Python代码(sklearn库) |
待续...