【机器学习速成宝典】模型篇05朴素贝叶斯【Naive Bayes】（Python版）

　　想象有 A、B、C 三个不透明的碗倒扣在桌面上，已知其中有（且仅有）一个瓷碗下面盖住一个鸡蛋。此时请问，鸡蛋在 A 碗下面的概率是多少？答曰 1/3。
　　现在发生一件事：有人揭开了 C 碗，发现 C 碗下面没有蛋。此时再问：鸡蛋在 A 碗下面的概率是多少？答曰 1/2。注意，由于有“揭开C碗发现鸡蛋不在C碗下面”这个新情况，对于“鸡蛋在 A 碗下面”这件事的主观概率由原来的 1/3 上升到了1/2。这里的先验概率就是 1/3，后验概率是 1/2。
也就是说“先”和“后”是相对于引起主观概率变化的那个新情况而言的。

条件概率公式、全概率公式、贝叶斯公式

　　条件概率公式：

　　在事件B发生的条件下，A发生的概率

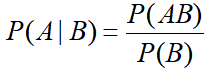
　　换一种写法：

　　理解了条件概率公式后，用一个引例介绍后面两个公式：村子里有三个小偷，事件B={村子失窃}，已知小偷们的偷窃成功率依次是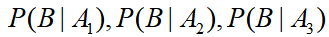，除夕夜去偷的概率依次是

　　全概率公式：

　　求：村庄除夕夜失窃的概率

　　贝叶斯公式：

　　求：在村子失窃的条件下，偷窃者是某个小偷的概率

什么是朴素贝叶斯(Naive Bayes)

　　引例

　　有一个训练集包含100个人，特征1是皮肤颜色（黑、黄）、特征2是个人资产情况（富、穷），标记是地区（非洲、亚洲）。在训练集中有60个非洲人（黑穷*47, 黑富*1, 黄穷*11, 黄富*1），有40个亚洲人（黑穷*1, 黄穷*32, 黄富*7）。请分别训练一个朴素贝叶斯模型。（作者这里不存在任何人种歧视的观点）

　　先计算先验概率：

　　再计算每一个特征的条件概率：

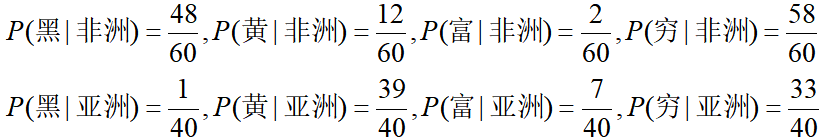
　　到此，已经完成了朴素贝叶斯模型所有参数的计算，模型学习完毕。

　　假设新来了一个人，他的特征是【[黑，穷]，地区=？】，请用朴素贝叶斯模型预测一下他的地区。

　　根据计算结果，模型会将这个人的地区预测为非洲。

　　二娃：你这个例子扯了这么半天，虽然我看明白了整套训练和预测的过程，可是，如何哪里体现了“朴素”和“贝叶斯”呢？

　　先说“朴素”，在例子中的体现就是：假设特征间是独立的（忽略皮肤颜色和资产情况的联系）。从而变成了“低配版的贝叶斯模型”，称为“朴素贝叶斯”。优点是可以减少需要估计的参数的个数；缺点是会牺牲一定的分类准确率。

　　再说“贝叶斯”，例子中公式的推倒都是朴素贝叶斯，如果是贝叶斯的话预测的公式是：

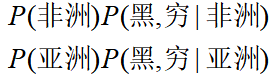
可以发现，朴素贝叶斯模型需要计算的参数个数为：

是线性增长的；而贝叶斯模型需要计算的参数个数为：

是指数增长的，实际是不可行的。

　　翠花：能不能用简练的语言叙述朴素贝叶斯的工作原理？

　　训练：先根据数据集，计算标记（地区）的先验概率，再计算每一个特征（肤色和财产）的条件概率。

　　预测：当一个训练集外的黑穷人来报道，假设特征间是独立的，朴素贝叶斯模型会预测他的老家是非洲的，原理就是“非洲人里黑人的比例 * 非洲人里穷人的比例 > 亚洲人里黑人的比例 * 亚洲人里穷人的比例”。这个乘积其实就是后验概率，贝叶斯模型会将实例分到后验概率最大的类中。

　　李航《统计学习方法》中的定义

　　朴素贝叶斯(naive Bayes) 法是基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的训练数据集，首先基于特征条件独立假设学习输入/输出的联合概率分布；然后基于此模型，对给定的输入x，利用贝叶斯定理求出后验概率最大的输出y。朴素贝叶斯法实现简单，学习与预测的效率都很高，是一种常用的方法。

拉普拉斯平滑(Laplace Smoothing)

　　继续上文的引例，考虑一个这样的问题：如果已知“某人的地区完全依靠其肤色的就能确定，资产情况是一个对判断地区没有参考价值的特征”，当来了一个黑穷人的时候，我们要算

如果根据训练集计算出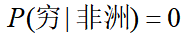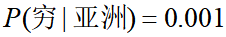，，发现(式1)<(式2)，则把一个黑穷人预测为亚洲人，分类产生偏差了。原因在于：如果出现某个要估计的概率值为0的情况时，会影响到后验概率的计算结果。

　　解决这一问题的方法是使用平滑操作，即令先验概率公式变为：

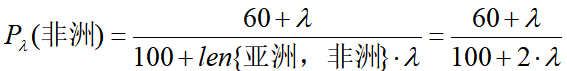
每个特征的条件概率公式变为：

　　式子中，等价于在随机变量各个取值的频数上赋予一个正数，当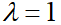时，称为拉普拉斯平滑。

　　这里附一个李航《统计学习方法》中的例子

应用：遇到连续变量怎么办？(多项式分布，高斯分布)

　　首先了解下多项式分布、正态分布

　　多项式分布：

　　我们扔一个骰子，重复扔n次，点数1~6的出现次数分别为(x1,x2,x3,x4,x5,x6)时的概率构成多项式分布。

　　正态分布（高斯分布）：

　　正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。

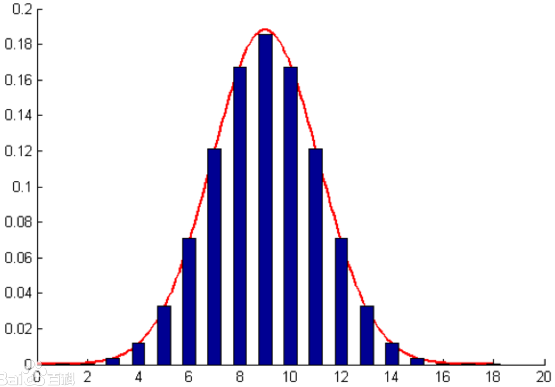
　　引例中的朴素贝叶斯模型假设特征的条件概率分布满足多项式分布。

　　当特征是连续变量的时候，运用多项式朴素贝叶斯分类器模型就会导致很多待估测的参数是0（不做平滑的情况下），此时即使做平滑，所得到的条件概率也难以描述真实情况。所以处理连续的特征变量，应该采用高斯朴素贝叶斯分类器模型（假设特征的条件概率分布满足正态分布）。

　　举个例子（维基百科）：

　　我们要做一个性别分类，观测的特征包括：身高、体重、脚的尺寸。

　　现有训练集：

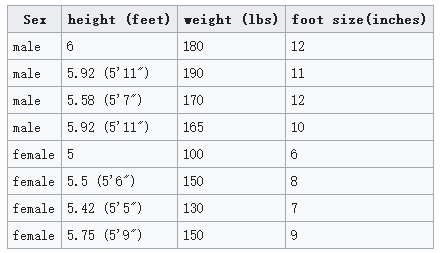
　　根据训练集计算一些参数：

　　要对测试集进行性别预测：

　　计算过程：

　　结果：预测为女性的概率高于预测为男性的概率，因此，将其预测为女性。

Python代码(sklearn库)

# -*- coding: utf-8 -*-
import numpy as np
from sklearn.datasets import load_iris
from sklearn import naive_bayes

iris = load_iris()
trainX = iris.data
trainY = iris.target
clf=naive_bayes.GaussianNB()  #高斯分布，没有参数
# clf=naive_bayes.MultinomialNB()  #多项式分布

clf.fit(trainX,trainY)
print "训练准确率:" + str(clf.score(trainX,trainY))
print "测试准确率:" + str(clf.score(trainX,trainY))

'''
训练准确率:0.96
测试准确率:0.96
'''

【机器学习速成宝典】模型篇05朴素贝叶斯【Naive Bayes】（Python版）

目录

先验概率与后验概率

条件概率公式、全概率公式、贝叶斯公式

什么是朴素贝叶斯(Naive Bayes)

拉普拉斯平滑(Laplace Smoothing)

应用：遇到连续变量怎么办？(多项式分布，高斯分布)

Python代码(sklearn库)