做题思路
简单想法
根据题意可以得出显而易见的结论:
在每次操作完成后,白球有 (x) 个时,黑球数量为 (n-x) 。于是我们设白球数量为 (x) 个。
对于本题的操作,仅有以下四种:
条件 (xge 1) :
- 取出一个白球,加入一对黑白球,取出一个白球
- 取出一个白球,加入一对黑白球,取出一个黑球
条件 (x<n) :
- 取出一个黑球,加入一对黑白球,取出一个白球
- 取出一个黑球,加入一对黑白球,取出一个黑球
那么我们可以想到一个简单的 DP :
设 (f_{i,j}) 为进行到操作 i 还剩 j 个白球的操作方案数,初始状态为
(f_{0,j}=1 , jin[0,n])
根据题意我们可以得到状态转移方程:
if(j>=1)
f[i+1][j-1]=f[i+1][j-1]+f[i][j],
f[i+1][j]=f[i+1][j]+f[i][j];
if(j<n)
f[i+1][j]=f[i+1][j]+f[i][j],
f[i+1][j+1]=f[i+1][j+1]+f[i][j];
但是这样转移显然有问题,因为当初始时白球数量不同时,进行相同的操作会得到相同的序列,而这种方案被我们进行了重复计算。
完善想法
那么问题变为了如何去除同一方案的重复贡献。
为了方便,我们将每次操作前后白球的数量变化画为折线,那么上文提到的操作可以用折线所表示:

那么假设我们对某种初始情况进行了操作 114314 (假设初始时白球数量为5),我们得到了以下折线:

显然,初始白球数量不同(折线起点纵坐标不同)且操作合法(操作期间白球数量(num_{white}in [0,n])) 我们在 DP 时发生了重复统计,反映到折线上(假设 (n=6) )就如下图所示:
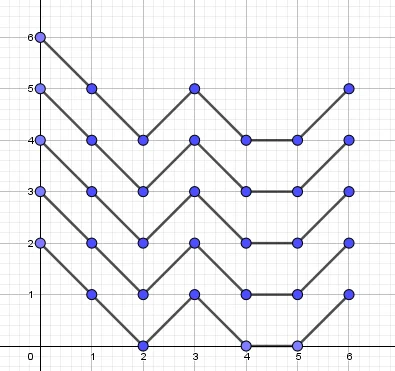
每一条折线所产生的颜色序列完全相同,但显然被统计了多次。
于是,我们产生了一个想法,对于每一种折线,只标记其中的一条,只统计它自己的贡献就行了。那么标记哪一条折线比较方便呢?
继续看上面的图,可以发现这些形状相同的折线唯一的不同点就是值域不同,于是就产生了一个做法: 我们只统计那些触碰到边界(与x轴接触的到折线)。
因为对于每一种形态且合法的折线,由于不同的起始点,所经历的纵坐标值域不同,仅有一条触碰到了x轴,其他折线均可以这条折线向上平移若干单位得到。
那么,我们可以将 DP 数组 (f_{i,j}) 多开一维变成 (f_{i,j,k}) ,(k)这一维表示这条折线是否接触到x轴,最后我们只需要统计 (sum^{n}_{j=0}f_{m,j,1}) 就行了
初始状态为 (f_{0,j,0}=1,jin [0,n] and f_{0,0,1}=1).
还有一点要注意的就是 j=1 时进行操作二时,折线其实是会接触到x轴的(第一步拿走一个白球会使白球数为0)
那么我们就能 偷税地 DP 了,
Code
#include<cmath>
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 3005
#define LL long long
using namespace std;
int n,m,f[N][N][2],ans;
const int mod = 1000000007;
inline int qr()
{
int x=0,w=1;char ch=0;
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*w;
}
inline int add(int a,int b){return a+b>mod?a+b-mod:a+b;}//让加法快一点(可能)
int main()
{
n=qr(),m=qr();
f[0][0][1]=1; //初始化部份
for(register int j=1;j<=n;j++) f[0][j][0]=1;
for(register int i=0;i<m;i++) //向后推操作
for(register int j=0;j<=n;j++) //枚举剩下多少个白球
{
if(j-1>=0)
{
//如果j==1时进行操作一和二会使折线接触到x轴(白球数变成0)
j==1 ? f[i+1][j-1][1]=add(f[i+1][j-1][1],f[i][j][0]) : f[i+1][j-1][0]=add(f[i+1][j-1][0],f[i][j][0]);//操作一
f[i+1][j-1][1]=add(f[i+1][j-1][1],f[i][j][1]);
j==1 ? f[i+1][j][1]=add(f[i+1][j][1],f[i][j][0]) : f[i+1][j][0]=add(f[i+1][j][0],f[i][j][0]);//操作二
f[i+1][j][1]=add(f[i+1][j][1],f[i][j][1]);
}
if(j+1<=n)
{
f[i+1][j+1][1]=add(f[i+1][j+1][1],f[i][j][1]);//操作三
f[i+1][j+1][0]=add(f[i+1][j+1][0],f[i][j][0]);
f[i+1][j][1]=add(f[i+1][j][1],f[i][j][1]);//操作四
f[i+1][j][0]=add(f[i+1][j][0],f[i][j][0]);
}
}
for(register int j=0;j<=n;j++)//累加答案
ans=add(ans,f[m][j][1]);
printf("%d
",ans);
return 0;
}