PCA,即主成分分析技术,又称主分量分析。主成分分析也称主分量分析,旨在利用降维的思想,把多指标转化为少数几个综合指标。
二维情况下,(物理意义)将坐标平面上的数据点投影在一个具有特征性的方向(向量)上,每个数据点在这个方向上的投影就是组成分。
在三维情况下,例如一个椭圆的立体点云,其组成分就是三个轴。
##组成分分析的应用
· 降维:例如将二维点投影到特征向量上,在特征向量上的数据点就成为了一维点,而且在最大程度上保留了原始信息。

· 法向量的估计
· 可以用来做分类
为了往后的证明,我们需明确几个概念
· 向量的内积(其实就是投影)
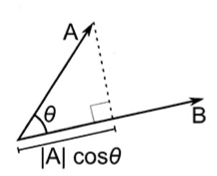
·一个矩阵跟一个向量的乘法

将矩阵的每一列进行了线性组合然后有了等式右边的内容。
也可以从SVD的角度去理解
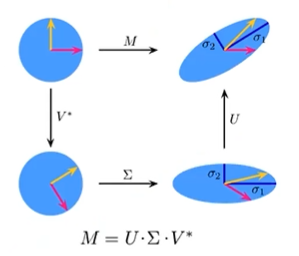
比如,一个矩阵可以分成U,西格玛∑,V*。
U和V*都是正交矩阵,类似于一个旋转矩阵一样的东西。
∑是一个对角矩阵。 对角矩阵:对角矩阵(diagonal matrix)是一个主对角线之外的元素皆为0的矩阵,常写为diag(a1,a2,...,an) 。对角矩阵可以认为是矩阵中最简单的一种。
∑就是在每个维度上进行了缩放。所以就是把一个圆变成了椭圆。
谱定理

关注要点:如果有一个对称矩阵A,那这个矩阵可以被分解为U lenda UT,跟我们刚刚看到的SVD是一样的,因为是一个对称矩阵,所以U和UT 是同一个U。
瑞利商定理

可从SVD的物理意义来理解他。
在XT和X之间插入了一个对称矩阵A,也就是经过XT和X来对原向量进行旋转缩放。
所以这个公式的意思就是,矩阵A可以扩大或缩小这个X多少倍。
因为旋转缩放不改变大小长度,所以范围是A的lendamin和lendamax
##瑞利商定理的证明

PCA的说明:
输入:高维空间里的一个向量,一堆高维的点,Xi 属于 R,i = 1,2,3,4...m。
输出:一堆主要的向量,例如Z1(最主要的向量,最有代表性的)Z2
1.什么叫做最主要的成分?
--如果我把这些高维点全部投影在某一个方向上,这些投影后的点的方差要最大,也就是这些点在那个方向上分布的非常散。
2.已经得到Z1,如何得到Z2?
--其实就是将已经得到的一堆数据点中是Z1的点去掉,再找剩下的东西里的最主要的成分。
往后同理。