题意
给定数组(h),求(max_{1le i<jle n}(h[i]+h[j])*(j-i)),(1le n,h[i]le 1e6)
分析
-
把原式改写为(max_{1le i<jle n}(h[i]-(-h[j]))*(j-i)),则对于每个平面点((i,h[i])),找到它右下角的点((j,-h[j]))使得面积最大。
-
对于(i_1<i_2),若(h[i_1]ge h[i_2]),则取(i_2)的地方取(i_1)一定更大,所以可以只取(i)从左至右升序排列的点。同理,对于(j_1<j_2),若(-h[j_1]ge -h[j_2]),则取(j_1)的地方取(j_2)一定更大,所以可以只取(j)从右至左降序排列的点。
-
对于点(i),若取(j)时取得最大值,则对于点(l<i),在([1-j])取得最大值;则对于点(r>i),在([j-n])取得最大值。所以可以利用决策单调性进行分治。
- 对于图中(l<i)的点来说,因为(j)比(k)优,所以(S_1ge S_2),得到(S_1+S3gt S_2-S_4)。则对于(l)来说,在(j)左侧取得最大值。同理可得点(r>i),在([j-n])取得最大值。
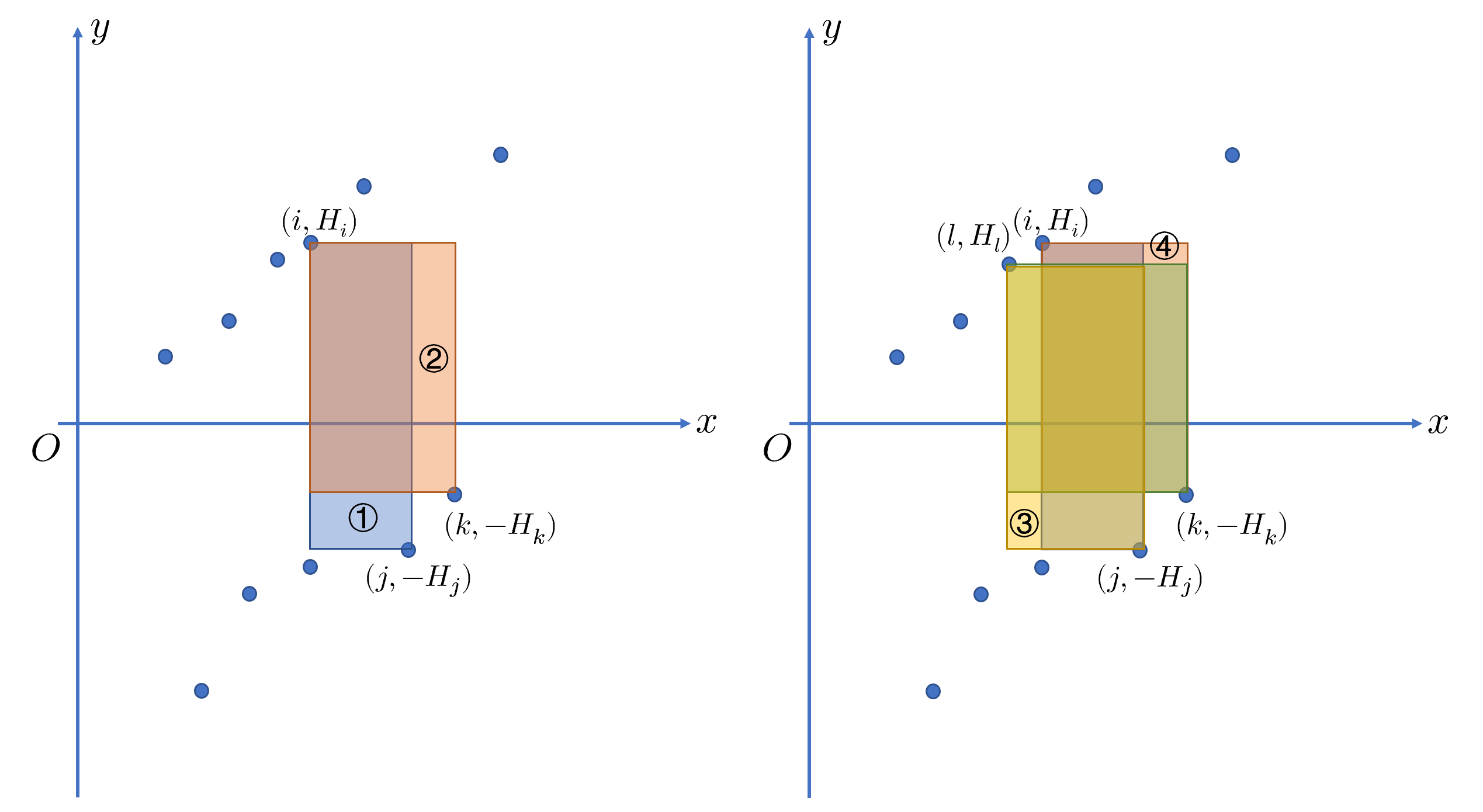
- 对于图中(l<i)的点来说,因为(j)比(k)优,所以(S_1ge S_2),得到(S_1+S3gt S_2-S_4)。则对于(l)来说,在(j)左侧取得最大值。同理可得点(r>i),在([j-n])取得最大值。
代码
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int maxn=1e6+5;
ll h[maxn],a[maxn],b[maxn],ai[maxn],bi[maxn],ans;
void proc(int l,int r,int L,int R)
{
ll Ans=0,id=L,mid=(l+r)/2;
for(ll i=L;i<=R;i++)
{
ll tmp=(a[mid]-b[i])*(bi[i]-ai[mid]);
if(tmp>Ans)
{
Ans=tmp;
id=i;
}
}
ans=max(ans,Ans);
if(l<mid)
proc(l,mid-1,L,id);
if(mid<r)
proc(mid+1,r,id,R);
}
void solve(){
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>h[i];
a[i]=h[i];
b[i]=-h[i];
}
int cnt=1,R=n;
ai[1]=1;
bi[n]=n;
for(int i=2;i<=n;i++)
{
if(a[i]>a[cnt])
{
a[++cnt]=a[i];
ai[cnt]=i;
}
}
for(int i=n-1;i>=1;i--)
{
if(b[i]<b[R])
{
b[--R]=b[i];
bi[R]=i;
}
}
ans=0;
proc(1,cnt,R,n);
cout<<ans<<'
';
}
int main()
{
ios::sync_with_stdio(false);
int t=1;
// cin>>t;
while(t--)
solve();
return 0;
}