算法导论数论素数测试和pollard整数因子分解

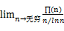1.素数定理：=1

2.欧拉定理：对n>1,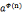=1(modn),对所有a属于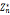成立

3.费马定理：p素数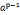，,=1(modp) 对所有a属于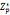成立

4.若n是素数=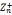

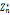
若n为合数，且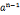=1(modn)，则n为伪素数

若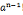=1(modn),则n定为合数

5. 对所有a属于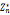，满足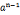=1(modn)合数为carmicheal数

    前一亿个数有255个carmicheal数，561,1105,1729

6.Miller-Rabin测试

1. 实验数个a
2. 计算每个模取幂时，注意最后一组平方里若有模n来说1的非平凡平方根，则为合数

注：（2）的原因

p 是奇素数x^2=1(mod p^e)且e>=1,则方程仅有两个解，x=1和x=-1（证明：http://www.cnblogs.com/inpeace7/archive/2012/03/12/2392292.html）

逆反命题： 模n存在1的非平凡平方根，n是合数

 

7.Witness(a,n)为真时，n为合数

8.n>2是一个奇数,n-1=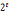u,u是奇数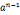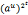，=,iß1 to t,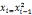(modn)

 

WITNESS(a,n)

{

        Let n-1=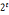u,u是奇数

        x0= MODULAR-EXPONENTIATION(a,u,n);

        for iß1 to t

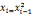            (modn);

            If(xi=1 && xi-1!=1 && xi-1!=n-1)

                Return 1;

        If(xt!=1)

            Return 1;

        Return 0;

}

MILLER-RABIN(n,s)

{

        for(jß 1 to s)

            a=RANDOM(1,n-1)

             if WITNESS(a,n)

                then return 合数

        return 质数

}

9.若n是一个奇合数，n为合数的证据至少为(n-1)/2

10.对任意奇数n>2,和正整数s，MILLER-RABIN(n,s),出错的概率至多为、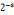

 

11.整数因子分解

Pollard 的启发式rho 算法

POLLARD-RHO(n)

{

    iß1

    x1ßRANDOM(0，n-1)

    yßx1

    kß2

    while(1)

{

    ißi+1

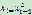        (modn)

    dßgcd(y-xi,n)

    if(d!=1 && d!=n)

        print d

    if(i==k)

        y=xi

        k=2k

}

}

常量储存空间，可只用一个x，时间复杂度：O(sqrt(n))