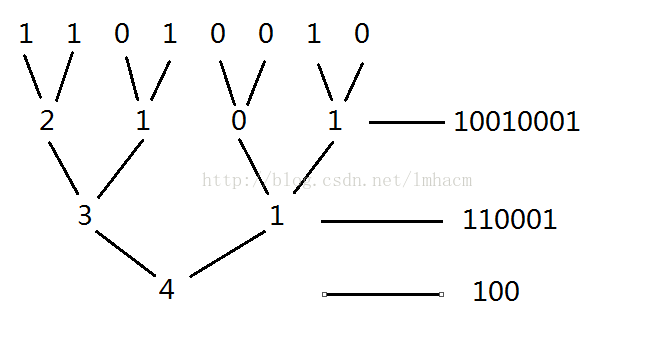这两天做一个粒子编辑器,某些参数设置用到一些位运算,特地查了一些相关技巧copy如下(尾附原文链接):
(一)概念
首先先对位运算都有哪些做一个介绍,位运算都是针对于二进制的计算方式,在计算时要转为二进制来处理。
(1)按位与
在C语言中用“&”符号来表示,运算时必须两个数都为1结果才为1,否则为0。
运算规则:0&0=0,0&1=0,1&0=0,1&1=1。
比如算5&9,先写为二进制变为0101&1001,每一位相应计算,得到0001,即5&9=1。
(2)按位或
在C语言中用“|”符号来表示,运算时只要有一个数为1,结果就为1,两个都是0时结果才是0。
运算规则:0|0=0,0|1=1,1|0=1,1|1=1。
比如算5|9,先写为二进制变为0101|1001,每一位相应计算,得到1101,即5|9=13。
(3)按位异或
在C语言中用“^”符号来表示,运算时如果两个数相同,则返回0,如果不相同则返回1。
运算规则:0^0=0,0^1=1,1^0=1,1^1=0。
比如算5^9,先写为二进制变为0101^1001,每一位相应计算,得到1100,即5^9=12。
(4)按位取反
在C语言中用“~”符号来表示,运算时将1变为0,0变为1。
运算规则:~1=0,~0=1。
*这里额外说一点,在计算机中,正数的二进制表示方法和普通的一样,而负数的二进制表示方法不同于普通的表示,在计算机中,负数以其正值的补码形式表达。
对于int型数而言,总共为32位数,比如对于5而言,写为二进制为00000000 00000000 00000000 00000101,这叫做5的原码。
将00000000 00000000 00000000 00000101每一位取反,得11111111 11111111 11111111 11111010,这个数叫做5的反码。
补码就是反码再+1,11111111 11111111 11111111 11111010 + 1 = 11111111 11111111 11111111 11111011,这个数叫做5的补码。
同样的,这个数就是-5的二进制表示。
比如算~5,先写二进制为11111111 11111111 11111111 11111010 + 1 = 11111111 11111111 11111111 11111011,每一位取反运算,得到11111111 11111111 11111111 11111010,即-6。
*所有正整数的按位取反是其本身+1的负数。
所有负整数的按位取反是其本身+1的绝对值。
零的按位取反是 -1。
(5)左移
在C语言中用“<<”符号来表示,运算时将这个数中的所有1向左移,空出的位补上0。
比如对于5<<2,表示5的二进制左移2位,先写为二进制为000101,左移后变为010100,即5<<2=20。
(6)右移
在C语言中用“>>”符号来表示,运算时将这个数中的所有1向右移,空出的位补符号位。(比如正数就补0,负数就补1)
比如对于5>>2,表示5的二进制右移2位,先写为二进制0101,右移后变为0001,即5>>2=1。
再比如对于-5>>2,表示-1的二进制右移2位,先写为二进制11111111 11111111 11111111 11111011,右移后变为11111111 11111111 11111111 11111110,即-5>>2=-2。
*位运算符的优先级为 按位取反(~)>左移(<<)=右移(>>)>按位与(&)>按位异或(^)>按位或(|)
(二)用于得到一些值
(1)获得2的n次方
位运算是通过二进制来表示的,所以只需要通过移动1就可以得到2的n次方的值。
1<<n;//2的n次方(2)乘/除2的值
-
n<<1;//n乘2
-
n>>1;//n除2
同理也可以计算乘/除任何2的次方的数的值
-
n<<2;//n乘4
-
n>>3;//n除8
-
n<<m;//计算n*(2^m)
-
n>>m;//计算n/(2^m)
(3)取余2的次方的数
因为2的次方用二进制来表示会成为1000...的形式,所以也可以通过按位与运算来进行取余,因为凡是后面不为0的为对应的都是余数。
-
n&3;//n取余4
-
n&((1<<m)-1);//n取余2^m
(4)取某个数的绝对值
因为在计算机中,负数是用补码表示的,所以如果这个数是负数,对这个数取反+1,就相当于还原了他的原码,也就是求出了这个负数的绝对值。所以对于一个负数n,利用~a+1就可以得到他的绝对值。然后再讨论一下,如果这个数是正数就不用进行处理,否则进行处理。
而判断正负也可以利用位运算,在后面(三)—(3)会提到,这样判断也可以利用位运算了。
再进一步分析一下,对于任何数,异或0会保持不变,异或1会改变,而上面判断正负得到的是0和-1(也就是全0和全1),这样的话再通过位运算来简化一下,将m设为n>>31(得到n的符号),然后用n^m,这样就能保证正数不变,负数改变。然后再来处理后面的+1,我们已经知道正数m为0,负数m为1,所以再在后面减去一个m就可以得到一个求绝对值的通式了。
-
m=n>>31;
-
return ((n^m)-m);
(5)取两个数的最值
首先为了得到大小关系,肯定还是要用n和m进行比较,也就是(n<m),那么如果不用比较运算符,仅用位运算,如何来实现取最值呢。我们知道,对于一个数,与任意一个给定的数连续异或两次,值不变(具体原因写在了(四)—(1))。所以利用这一点,我们先写一个式子m^(n^m),如果要取m的值就不继续计算后面的(n^m),如果取n的值就计算这个整体式子。
那么如何判断是否计算后面的式子呢。我们先来分开看一下,如果n>m的话,(n<m)应返回0,这样将后面的(n^m)&0就可以不再计算。如果n<m的话,(n<m)应返回1,但是通过1我们无法让式子正常的进行计算,所以我们还是取负值-1,也就是二进制全1,这样继续进行按位与运算就不会影响计算。所以综上所述,最后我们就可以把式子写成(m^(n^m)&-(n<m))。
同理我们也可以得到取最大值的方法。
-
(m^(n^m)&-(n<m))//取最小值
-
(n^(n^m)&-(n<m))//取最大值
(6)取两个数的平均值
普通的取平均值是(n+m)/2,所以位运算当然就可以写成(n+m)>>1......额,好吧,要是这么简单我也不会再多写出一块了。这里利用位运算,主要的目的是为了防止n+m导致的数据溢出。那么,我们如何在保证不溢出的情况下来得到平均值呢。
因为对于一个其他进制的数,都可以分解为各个位与其权的乘积的和,所以我们针对这个进位来去考虑如何得到平均值。
首先我们先来考虑两个位置上的数是相同的,假如是两个0我们当然不必再计算了,如果是两个1,那么就相加之后除2的结果仍然是1,因为在1后面再加就要进位了,所以我们这里不再进行进位,而是直接取1就可以了,这种情况我们用n&m就可以得到(就算两位是不相同的,0&1=0,我们也视为仍未处理)。
然后我们再来处理对于两个数不同的情况,一个1一个0,那么这里就没有进位的关系了,所以我们直接将1右移1位,也就是将这个和除2,就可以得到这个位置上的平均值,所以我们采用(n^m)>>1的方式来得到结果。(用异或的原因是为了去除掉两个数相同的情况,这样结果为0,我们就可以视为未处理)。
之后再将处理好的这两部分加起来就可以了。
(a&b) + ((a^b) >> 1)(7)取int型的最值
在计算机中,对于int型的最大值,也就是符号位为0,其余位赋值为1,这样直接(1<<31)-1就可以得到。
同样的,对于int型的最小值,也就是符号位为1,其余位赋值为0,这样用(1<<31)直接可以得到答案。
对于long long型取最值也可以用同样的方法,不过这样位数就要移动63位。
-
(1<<31)-1;//int的最大值
-
(1<<31);//int的最小值
-
((long long)1<<63)-1;//long long的最大值
-
((long long)1<<63);//long long的最小值
(三)一些条件判断
(1)判断一个数为奇数还是偶数
因为二进制逢二进位,所以很显然最后一位决定了这个数的奇偶性,直接按位与1就可以判断出这个数的奇偶性了。
-
if(n&1)
-
{
-
//n是奇数
-
}
-
else
-
{
-
//n是偶数
-
}
(2)判断两个数符号是否相同
这个也很简单,二进制第一位表示符号,所以符号相同就为0(正数),符号不同就为1(负数)。
-
if(n^m>=0)
-
{
-
//n和m同符号
-
}
-
else
-
{
-
//n和m不同号
-
}
(3)判断一个数的正负
因为二进制的第一位为这个数的符号,所以只需要把第一个数提取出来就可以知道正负了,直接右移31位即可。
-
if(n>>31)
-
{
-
//n为正数
-
}
-
else
-
{
-
//n为负数
-
}
(四)一些特殊用法
(1)交换两个数
普通的交换两个数很常见,直接用一个中间变量temp,然后进行互换就可以了。不过如果现在要求不用中间变量,只用a和b这两个变量如何交换?就要用位运算来实现了。
-
a^=b;
-
b^=a;
-
a^=b;
可以这样做的原因是因为通过异或能使原数中的异或1的位改变(1^1=0,0^1=1),异或0的位不变。而若再进行一次操作,我们会发现,这些位又会翻转回去(0^1=1,1^1=0),这就意味着一个数与任意一个给定的数连续异或两次,值不变。
这样的话再回来看这个式子,我们会发现b=a^b^b,a=a^b^a,所以第一句a赋为a^b,之后再相互异或就可以交换了。
(2)对这个数二进制的第m位进行处理(从低位到高位)
首先为了得到第m位的值,肯定是要将这个数右移(m-1)位,然后为了将其他多余的数清零,我们再进行&1的操作,就可以将第m位提取出来了。
如果是想改变第m位的值,那么就不能对这个数进行移动,因为这样会改变这个数的值。所以我们要对1向左移(m-1)位,然后再进行操作更改。如果要将第m位变成1,那么就n|(1<<(m-1)),这样就可以保证其余位不变改变第m位。如果要将第m位变为0,那么就n&~(1<<(m-1)),因为取反后就能得到除了第m位为0其余位都为1的一个数,这样再进行按位与计算就可以只改变第m位的值了。
-
(n>>(m-1))&1;//取n的二进制的第m位
-
n|(1<<(m-1));//将n的二进制的第m位改为1
-
n&~(1<<(m-1));//将n的二进制的第m位改为0
(3)计算一个数二进制中1的个数(BitCount算法)
这里算法本以为就简单的两种算法,一搜发现原来有好多....
①普通算法
为了得到这个数二进制中有多少个1,可以依次从后向前找是不是1,然后全部遍历一遍,方法是可以通过将一个数flag赋为1,然后用这个数与要计算的数进行按位与计算,如果得到的结果不为0,则说明这一位是有一个1的,否则为0。然后再将flag向左移,一直左移到最大位,就可以将这个数中的所有1都筛出来了。
-
int bitcount1(int n)
-
{
-
int cou=0;
-
int flag=1;
-
while(flag)
-
{
-
if(n&flag)
-
{
-
cou++;
-
}
-
flag=flag<<1;
-
}
-
return cou;
-
}
②快速算法
但是这样的话,每次找总共有几位必须要通过这个类型最大位数的遍历次数才可以找到答案。所以这里还可以再优化一下加快一下速度。假设我们要求的数是n,那么我们将n-1,就可以将n的二进制变为最后一位的1变为0,最后一位的1右边的0全部变为1的一个数。这样重复计算n=n&(n-1),计算的次数就是n这个数二进制中1的个数。
-
int bitcount2(int n)
-
{
-
int cou=0;
-
while(n)
-
{
-
n=n&(n-1);
-
cou++;
-
}
-
return cou;
-
}
③平行算法
除此之外还有一种方法是可以通过一种平行算法来做,将这个数每一位拆开来看,然后相邻的位进行相加计算,最后得出的结果就是1的个数。过程如下图:(在计算的时候依然还是用二进制的方式来进行存储,这里拿210这个数来举例)
那么,我们怎么来实现这个相邻位相加呢。我们可以通过按位与的运算来分隔开相邻的位数,也就是一开始用10101010和01010101来计算得到,之后用11001100和00110011计算,依次类推,就可以模拟这样一个相加的过程。为了方便表示这些数,我们用16进制来进行表示,因为int型是32位,所以只需要计算最多5次就可以得出答案。
-
int bitcount3(int n)
-
{
-
n=(n&0x55555555)+((n>>1)&0x55555555);
-
n=(n&0x33333333)+((n>>2)&0x33333333);
-
n=(n&0x0f0f0f0f)+((n>>4)&0x0f0f0f0f);
-
n=(n&0x00ff00ff)+((n>>8)&0x00ff00ff);
-
n=(n&0x0000ffff)+((n>>16)&0x0000ffff);
-
return n;
-
}
④查表法
当然也可以通过打表的方式,我们可以将这个数来分开,总共是32位的数,那么我们就分成4位4位的来看,打一个4bit的表出来,然后每4位进行一下查询在这四个数中有几个1,然后直接输出就可以了。同理我们也可以打更大的表来追求更快的速度,8bit表,16bit表甚至32bit表,只要你有耐心的话→_→
-
int bitcount4(int n)//4bit表
-
{
-
int table[16] =
-
{
-
0,1,1,2,
-
1,2,2,3,
-
1,2,2,3,
-
2,3,3,4
-
};
-
int cou=0 ;
-
while(n)
-
{
-
cou+=table[n&0xf];
-
n>>=4;
-
}
-
return cou;
-
}
-
-
int bitcount5(int n)//8bit表
-
{
-
int table[256] =
-
{
-
0,1,1,2,1,2,2,3,1,2,2,3,2,3,3,4,
-
1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,
-
1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,
-
2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,
-
1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,
-
2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,
-
2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,
-
3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,
-
1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,
-
2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,
-
2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,
-
3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,
-
2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,
-
3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,
-
3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,
-
4,5,5,6,5,6,6,7,5,6,6,7,6,7,7,8,
-
};
-
int cou=0;
-
while(n)
-
{
-
cou+=table[n&0xff];
-
n>>=8;
-
}
-
return cou;
-
}
⑤MIT HAKMEM算法
如果将一个二进制数还原成一个十进制数,那么我们只需要计算一个多项式a0*2^0+a1*2^1+a2*2^2+...所以我们会发现,如果要求二进制中1的个数的话,只需要将找个多项式的权消去,变为a0+a1+a2+...的形式就可以得到这个个数了。
我们将要求的n转为一个二进制数,然后每3位分为一组,这样的话每一组的值就是4a+2b+c,因为都是2的倍数增长,所以我们可以将这个数除2,也就是右移1位,得到2a+b和a,然后进行相减运算就可以得到a+b+c,这样我们进行的第一步处理就可以得到一个式子tmp=n-((n>>1)&033333333333)-((n>>2)&011111111111);
不过在相加的过程中会出现一些重复的部分,因为tmp是将相邻的组相加,这样肯定会出现重复的部分,所以将这部分重复处消去。而在计算的时候因为是6bit相加一次,所以结果最后还要取余63得到最后的结果。
这样两行代码就可以得到最后的结果,也许速度不是最快的一种,但这是最为简洁的一种代码。
-
int bitcount6(int n)
-
{
-
int tmp=n-((n>>1)&033333333333)-((n>>2)&011111111111);
-
return ((tmp+(tmp>>3))&030707070707)%63;
-
}
算法参考博客: http://www.cnblogs.com/graphics/archive/2010/06/21/1752421.html#!comments
http://blog.csdn.net/msquare/article/details/4536388
(4)查找一个数组中一些数字出现次数不同于其他数的问题
①一个数组里除了一个数字出现一次之外,其他的数字都出现了两次。
这是这类题目中最简单的一种情况,我们之前已经知道了,一个数异或自己也就等于0,所以我们只需要将整个数组一个一个全部异或,最后得到的那个数就是只出现了一次的那个数字了。因为那些出现了两次的数字全部都被抵消掉了。
-
int find_1_1_2(int n)
-
{
-
int i;
-
int ans=0;
-
for(i=0;i<n;i++)
-
ans^=a[i];
-
return ans;
-
}
②一个数组里除了两个数字出现一次之外,其他的数字都出现了两次。
因为这次有了两个数字,所以直接全部异或肯定是得不到结果的,所以就想如果可以把这堆数组分成两堆,一堆中一个出现一次的数,那么就可以化成上面的问题,也就变得更好处理了,但是如何分才能分出这两组呢。我们知道一个数异或自己等于0,所以现在将所有数异或了之后得到的值就是这两个出现一次的数异或所得的值。现在再拿出来利用这个值,因为这是两个数异或的结果,所以我们找出这个结果中第一个为1的位置来,那么这个位置我们就可以说是这两个数的区别了(一个数在这个位置上为0,另一个数在这个位置上为1,因为这两个数不同,所以肯定能找到这样的一位)。
然后我们就可以根据这个区别来分出两组,一组是这一位为1的数构成的数组,另一组是这一位为0的数构成的数组,区分开两个数组之后再分别异或,就能得到这两个数了。
-
int find_2_1_2(int n)
-
{
-
int i;
-
int ans=0;
-
int ans1=0,ans2=0;
-
for(i=0;i<n;i++)
-
ans^=a[i];
-
-
int pos=0;
-
while(((ans>>pos)&1)!=1)
-
pos++;
-
-
for(i=0;i<n;i++)
-
{
-
if(((a[i]>>pos)&1)!=1)
-
ans1^=a[i];
-
else
-
ans2^=a[i];
-
}
-
cout<<ans1<<" "<<ans2<<endl;
-
return 0;
-
}