例子：一块长方形的金属板，四个顶点的坐标是(1,1)，(5,1)，(1,3)，(5,3)．在坐标原点处有一个火焰，它使金属板受热．假定板上任意一点处的温度与该点到原点的距离成反比．在(3,2)处有一个蚂蚁，问这只蚂蚁应沿什么方向爬行才能最快到达较凉快的地点？问题的答案：应沿由热变冷变化最骤烈的方向（即梯度方向）爬行．
梯度
在矢量微积分中，标量场的梯度是一个矢量场。标量场中某一点上的梯度指向标量场增长最快的方向，梯度的长度是这个最大的变化率。在单变量的实值函数的情况，梯度只是导数，或者，对于一个线性函数，也就是线的斜率。梯度的解释假设有一个房间，房间内所有点的温度由一个标量场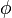
给出的，即点
的温度是
。假设温度不随时间改变。然后，在房间的每一点，该点的梯度将显示变热最快的方向。梯度的大小将表示在该方向上变热的速度。
考虑一座高度在
点是
的山。
在一点的梯度是在该点坡度（或者说斜度）最陡的方向。梯度的大小告诉我们坡度到底有多陡。
梯度也可以告诉我们一个数量在不是最快变化方向的其他方向的变化速度。再次考虑山坡的例子。可以有条直接上山的路其坡度是最大的，则其坡度是梯度的大小。也可以有一条和上坡方向成一个角度的路，例如投影在水平面上是60°角。则，若最陡的坡度是40%，这条路的坡度小一点，是20%，也就是40%乘以60°的余弦。
这个现象可以如下数学的表示。山的高度函数的梯度点积一个单位矢量给出了表面在该矢量的方向上的斜率。这称为方向导数。
上面两个图中，标量场是黑白的，黑色表示大的数值，而其相应的梯度用蓝色箭头表示。形式化定义一个标量函数
的梯度记为：
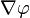或 
（在三维情况，该表达式在直角坐标中扩展为
虽然使用坐标表达，但结果是在正交变换下不变，从几何的观点来看，这是应该的。
范例函数
的梯度为：
,
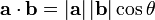梯度下降法，基于这样的观察：如果实值函数 
在点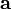 
处可微且有定义，那么函数 
在 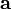点沿着梯度相反的方向 
下降最快。
因而，如果
对于 
为一个够小数值时成立，那么 
。
考虑到这一点，我们可以从函数 F 的局部极小值的初始估计 
出发，并考虑如下序列 
使得
因此可得到
如果顺利的话序列 
收敛到期望的极值。注意每次迭代步长 
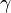可以改变。
下侧的图片示例了这一过程，这里假设 
定义在平面上，并且函数图像是一个碗形。蓝色的曲线是等高线(水平集)，即函数 为常数的集合构成的曲线。红色的箭头指向该点梯度的反方向。（一点处的梯度方向与通过该点的等高线垂直）。沿着梯度下降方向，将最终到达碗底，即函数 值最小的点。
有关梯度下降法的描述
数量积
在欧几里得空间中，点积可以直观地定义为
这里 |x| 表示x的范数（长度），θ表示两个矢量之间的角度。
注意：点积的形式定义和这个定义不同；在形式定义中，a和b的夹角是通过上述等式定义的。
这样，两个互相垂直的矢量的点积总是零。若a和b都是单位矢量（长度为1），它们的点积就是它们的夹角的余弦。那么，给定两个矢量，它们之间的夹角可以通过下列公式得到：
- ********
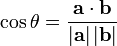*****可求2个向量的夹角***** 
这个运算可以简单地理解为：在点积运算中，第一个矢量投影到第二个矢量上（这里，矢量的顺序是不重要的，点积运算是可交换的），然后通过除以它们的标量长度来“标准化”。这样，这个分数一定是小于等于1的，可以简单地转化成一个角度值。
需要注意的是，点积的几何解释通常只适用于
(
)。在高维空间，其他的域或模中，点积只有一个定义，那就是
点积可以用来计算合力和功。若b为单位矢量，则点积即为a在方向b的投影，即给出了力在这个方向上的分解。功即是力和位移的点积。
==============
方向导数：讨论函数z=f（x，y）在P沿某一方向的变化率问题
梯度：方向导数最大的方向。 （例如 电压递增方向）
恒定值方向：方向导数为0的方向，与梯度成90度夹角,cos（90度）=0。（例如 恒转矩方向）