省选模拟21#
A. 灯##
题意: n=m=q=1e5
题解:根号算法平衡复杂度。首先把相连的同色块缩成一个
对于数量<√n的颜色采取暴力更新的手段;
对于数量>√n的颜色如果可以O(1)得到答案;每次更新完一种颜色后更新根号种大块的答案。
具体的,记录每种颜色左右下标的颜色,以及小块颜色所有的位置下标。对大块处理出一个数组res表示改变这个大块的状态时能,+-num-res就是这个大块的贡献。
考虑如何计算出这个res。
考虑添加一个颜色时它左右的大块颜色都会加一的贡献:添加时会减少1的贡献,删除时会增加1的贡献。
考虑删除一个颜色时它左右的大块颜色都会减一的贡献:添加时会增加1的贡献,删除时会减少1的贡献。
一个下标的贡献可以是1 0 -1,这是有0 1 2个元素相邻时的贡献。
很经典的根号做法,难度在于想不到res这个数组以及更新时也会很难想。
B. 十字路口##
题意:
题解:在这m次观察中,同一个灯不同的红灯状态之间连观察的边(根据红灯给观察连边),如果成环了就说明是周期的整数倍。
暴力就是O(n^2m)条边,正解优化边数,按权值排序后直接相邻连环一定是答案。
C. 密室逃脱##
题意:n=1000 m=10000
题解:考虑一般形态一定是隧道被划分成了若干段,每段由若干小段组成。不妨设f[[i][j]为考虑到第i个隧道恰好能留j个人时前i个隧道的最大人数。
本题题解的性质是“每个房间能留下的人数是固定的”
转移就很简单了.
j<a[i] f[i][j]->f[i+1][j+b[i]],f[i+1][0~b[i]-1]
a[i]<=j<a[i]+b[i] f[i][j]->f[i+1][j-a[i]]
a[i]+b[i]<=j<=20000 f[i][j]->f[i+1][j]
p.s. 上界要开到两倍m emmm
难度在于dp定义以及这个dp定义的性质。
省选模拟22#
A. 遮天蔽日##
题意:地球周围有个多边形,多边形自转+绕地球公转,求太阳某一时刻找到地球上的弧长。
题解:用三角剖分求重心的方式求出多边形的重心大致就是从第二个顶点开始相邻的和第一个节点组成的三角形的重心按面积带权平均。
把一个点绕着中心旋转theta:用两点距离和横坐标差,反三角函数倒出原向量与x轴正半轴的夹角,再+/-theta。
求切线:用两点间距离和半径倒出夹角,然后使两点连线旋转theta,求这条直线与圆的交点。
求垂足:先算叉积除以底就是距离,然后可以求出点到顶点的一条长度=距离的向量,再用上面旋转的方法求出此向量
求交点:求完垂足再进行类似的操作就有了交点...
B. 三元组##
发现题目是一个求双回文串个数,manacher求出以之为起点终点的方案再一拼就好了,用差分来实现这个过程。
C. 最有价值##
发现一个物品的价值只会被统计一次,所以大概是网络流。
物品权值有正有负,有“选我必须选他”的样子就是最大权了。
省选模拟23#
A. Expectation##
两个部分分是链和菊花。
链的答案是0.5*(n-1),菊花不会。
这道题考试时题意读不懂。
B. Sequence##
题意:在线求区间本质不同的子序列个数。n=1e6
题解:首先一个显然的dp:设f[i][j]表示考虑到i,以j字符结尾的子序列的个数
那么转移f[i]艹
C.##
省选模拟24#
A. U.N.OWEN就是她吗?##
考试时有个费用流的思路,但是爆0了,考后看到有人拿这个得了60分,应该是自己打错了,但看不出来.
题意:n堆石子,每堆石子有ai个,m次指令,每次指令要求把li,ri内的石子拿ki个,如果不够可以全拿,求拿的石子的最大字典序。保证区间互不包含。n=3e5 m=3e5 ai=500 ki=10000
题解:好神的霍尔定理用法啊,没想到它还能这样用...
把指令按照li排序,把每个指令拆成ki个,把每堆石头拆成ai个。设每个指令的答案为B[i],那么用霍尔定理检验的话就是检验是由有完美匹配。
由于题目保证互不包含,因此如果使用霍尔定理的话,原定理:“如果X存在完美匹配,那么对于任意子集|S|和对应的连边集合|T|都有|S|<=|T|。“
就可以将任意子集转化成连续的几个指令,原因:考虑不连续的若干个指令,这里只考虑两个的情况,大于两个的情况可以连续的指令两两间考虑来达到目的。
如果说这两个指令的区间相离,只需要检验分别这两个指令是否合法;
如果两个指令相交,那么由于互不包含的特殊性质,把这两个指令中间的指令加入|S|,|T|不变,这时的条件比原条件更为苛刻。
对于每次指令,是要求所有包含这个指令的区间都符合条件,即
线段树上维护每个点最大的sumB[i]-sumA[R[i]]与最小的sumB[i-1]-sumA[L[i]-1],查询时查询max p[i]~m sumB[i]-sumA[R[i]],min 1~p[i] sumB[i-1]-sumA[L[i]-1],再用min-max就是答案。
要和ki取min。
复杂度O(mlog)。
B. 哈德曼的妖怪少女##
不会枯了
C. 平安时代的外星人##
题意:同圈地游戏。
题解:可以发现(?)最终路线一定不会穿过从起点到每个特殊点的左上端点的最短路,如果穿过就完全可以顺着最短路走。
所以需要找到一条包裹所有最短路的环,使得环长最小。
那么对每个点建出四个点
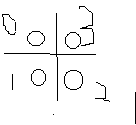
然后对应的向四周连边
假如说有某条边不能经过,那么它上下(左右)的两个点就不能连边(如上边的边lim=1,则0 3不能连边,表示不能这样走)
注意,特殊点由于不能经过,因此特殊点内部的四个点不能连边。
注意,(1,1)的(0,1),(0,3)不能连边,答案就是s=(1,1,3)t=(1,1,1)的最短路。
细节还行,打完后一遍过的。
省选模拟25#
1.环##
?
可以证明若k,n不互质一定无解.
设所有1的下标和为(x)
(x+akequiv x+1 (mod n))
(akequiv 1 (mod n))
(ak | n+1 (mod n))
题解给出了一种精妙的构造方法:
对于第(i)个串令其为(frac{i}{k}.....frac{i+k-1}{k})
A类型显然右移(frac{1}{k})即可.
B类型:
由于(frac{i}{k}+1=frac{i+1+k-1}{k}frac{i+k}{k}>frac{i+k-1}{k})所以为0.
移动(frac{i}{k})那一位,就变成了i+1的最后一位.
2.DNA序列##
选择排序
假如知道顺序,倒序,贪心的选择最小的前缀一定会得到最小字符串.
3.探寻##
贪心
有个打怪兽的经典思路.
设消耗为a,补给为b.
定义一个二元组为(a-b,a).
我们要最小化x的最大值.
第二维是最
(if(x1*x2<0)) 先选x负的.
(if(x1<0&&x2<0)) 选择y小的.
(if(y1>0&&y2>0)):
若((x,y))在((dx,dy))前面更优
则(max(x+dy,y)<max(dx+y,dy))
(x+dy<dx+y)
(x-y<dx-dy)
所以选x-y小的.
若全局最优的父亲已经和1节点连上了,下一个一定是选它的.
若没有,就把它和父亲合并,因为全局最优保证了选完父亲一定就选它.
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=2e5+7;
const ll inf=1e15;
int n,ed;
int f[N],fa[N],vis[N];
struct node{
ll x,y;
int id;
friend bool operator < (node a,node b){
if(a.x >=a.y&&b.x>=b.y) return a.y==b.y?a.id<b.id:a.y<b.y;
if(a.x>=a.y) return 1;
if(b.x>=b.y) return 0;
return a.id<b.id;
}
}p[N];
inline int find(int x){
return fa[x]==x?x:fa[x]=find(fa[x]);
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i) fa[i]=i,p[i].id=i;
for(int i=2;i<=n;++i){
scanf("%d%lld%lld",&f[i],&p[i].x,&p[i].y); ++f[i];
if(p[i].x==-1) p[i].x=inf,ed=i;
}
set<node> s;
for(int i=2;i<=n;++i) s.insert(p[i]);
ll now=0,ans=0; vis[1]=1;
while(1){
int x=s.begin()->id,y=find(f[x]); s.erase(p[x]);
if(vis[y]){
if(p[x].y>now) ans+=p[x].y-now,now+=p[x].y-now;
now-=p[x].y; now+=p[x].x;
vis[x]=1;
if(find(x)==find(ed)) break;
}
else{
s.erase(p[y]);
ll sum=p[y].x+p[x].x-p[y].y-p[x].y;
p[y].y=max(p[y].y,p[y].y-p[y].x+p[x].y);
p[y].x=p[y].y+sum;
fa[x]=y; s.insert(p[y]);
}
}
printf("%lld
",ans);
return 0;
}
省选模拟26#
A. 染色问题##
dp+多项式(我不喜欢的类型)
设dp[i][j]表示考虑前i种颜色覆盖了j个格子的方案数.
首先列出普通的dp式子(虽然对我来说很大神吧)
接着考虑dp[0][0]对dp[m][n]的贡献.
设经过的序列长度为k,其实就是最终格子上有k种颜色.
首先,前边的dp[i-1][j]可以通过组合数C(m-1,k-1)来统计,原理大致上是....(好吧其实现在我不知道以后再补).
后面的系数相当于序列的每一项+1乘起来.
那么如果我们构造出一个多项式$$prodlimits_{i=2}^n(x+i)$$
它第n-k项的系数就是相当于在[1,n-1]中任意选择了(n-1-(n-k))=k-1项作为序列每一项然后还乘上了每一项+1.
为什么只选择k-1项呢?因为最后一次涂颜色一定会涂上格子所以不能选择(我莫得选择)
那么分治FFT可以做到O(nlog^2)了.只有80分.
考虑已知(F_t(x)=prodlimits_{i=1}^{2^t}(x+i)),如何求出(F_{t+1}(x)).
发现(F_{t+1}x=F_t(x)F_t(x+2^t)).
所以就可以只递归左边右边拆掉((x+2^t)^i)二项式定理展开了.
可能右边比左边项数多一,再把多出来的那一项暴力FFT上去.
复杂度O(nlog).
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=2e6+50;
const int mod=998244353;
int n,m,rev[N];
int fac[N],finv[N],inv[N],BIT[N],a[N],b[N],c[N],d[N];
ll mgml(ll a,ll b,ll ans=1){
for(;b;b>>=1,a=a*a%mod) if(b&1) ans=ans*a%mod;
return ans;
}
ll C(int x,int y){return (x<y||y<0)?0:1LL*fac[x]*finv[y]%mod*finv[x-y]%mod;}
void NTT(int *a,int len,int opt){
for(int i=0;i<len;++i){
rev[i]=(rev[i>>1]>>1)|((i&1)<<BIT[len]-1);
if(i<rev[i]) swap(a[i],a[rev[i]]);
}
for(int i=1;i<len;i<<=1)
for(int j=0,wn=mgml(3,(mod-1)/(i<<1));j<len;j+=i<<1)
for(int k=0,w=1,x,y;k<i;++k,w=1LL*w*wn%mod)
x=a[j+k],y=1LL*w*a[j+k+i]%mod,a[j+k]=(x+y)%mod,a[j+k+i]=(x-y+mod)%mod;
if(opt==1) return;
reverse(a+1,a+len);
for(int i=0,Inv=mgml(len,mod-2);i<len;++i) a[i]=1LL*a[i]*Inv%mod;
}
void solve(int l,int r){
if(l==r) return a[0]=l,a[1]=1,void();
int mid=(l+r)>>1;if(mid-l+1>r-mid) mid--;
int t=mid-l+1,len=1<<(int)(log2(t*2+2)+1);solve(l,mid);
for(int i=0;i<len;++i) b[i]=c[i]=0;
for(int i=0;i<=t;++i) b[i]=1LL*a[i]*fac[i]%mod;
for(int i=0,powt=1;i<=t;++i,powt=1LL*powt*t%mod) c[i]=1LL*powt*finv[i]%mod;
reverse(c,c+t+1);
NTT(b,len,1);NTT(c,len,1);for(int i=0;i<len;++i) b[i]=1LL*b[i]*c[i]%mod;NTT(b,len,-1);
for(int i=0;i<=t;++i) b[i]=1LL*b[t+i]*finv[i]%mod;for(int i=t+1;i<len;++i) b[i]=0;
if(r-mid>mid-l+1){
for(int i=0;i<len;++i) c[i]=0;
c[0]=r;c[1]=1;NTT(b,len,1);NTT(c,len,1);for(int i=0;i<len;++i) b[i]=1LL*b[i]*c[i]%mod;NTT(b,len,-1);
}
NTT(a,len,1);NTT(b,len,1);for(int i=0;i<len;++i) a[i]=1LL*a[i]*b[i]%mod;NTT(a,len,-1);
}
int main(){
scanf("%d%d",&n,&m);
fac[0]=fac[1]=inv[0]=inv[1]=finv[0]=finv[1]=1;
for(int i=2;i<N;++i) fac[i]=1LL*fac[i-1]*i%mod,inv[i]=1LL*inv[mod%i]*(mod-mod/i)%mod,finv[i]=1LL*finv[i-1]*inv[i]%mod;
for(int i=0,j=1;j<N;++i,j<<=1) BIT[j]=i;
solve(2,n);
int ans=0;
for(int i=1;i<=m;++i) if(n-i>=0) ans=(ans+1LL*C(m-1,i-1)*a[n-i]%mod)%mod;
printf("%d
",ans);
return 0;
}
2.芬威克树##
3.礼物##
Burnside+插板容斥
环长n,选择m个特殊位置,连续长度不能超过k.
n=m=k=1e6
还是考虑一个循环节长度(d|gcd(n,m))
(gcd(i,n))是长度,那么由于环内要求等价,所以(frac{n}{gcd})就成了一组方案的关键,其他的都听它的.
然后之前那道(n^2)题的思路已经不可行了.
不过由于给定特殊位置的数量,反而更好做?(对我不是)
由于m<n所以对于一个循环节必然会有位置是0.
我们强制让他作为我们考虑的初始位置.
然后考虑这种情况占总情况的方案数.
按照(secret)的讲述,首先的问题.长为n的环,选m个位置涂黑,问选到第一个位置是白的概率?
(frac{n-m}{n})
问:第一个位置是白色的概率是否等于(frac{第一个位置是白色的方案数}{第一个位置是白色/黑色的方案数})?
是.
那么第一个位置是0的概率是(frac{n-m}{n}),占总方案数的(frac{n-m}{n}).
现在只需要统计出来第一个点为0的方案数.
现在就可以拆环了因为保证第一个点为0所以环不会有任何的影响.
有n-m个0,m个1,要求每段1的长度<=k,求方案数.
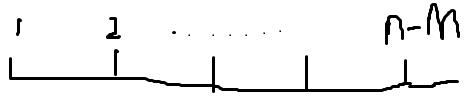
插板容斥,就是枚举几个不合法的段落计算出答案.
#include<cstdio>
#define ll long long
using namespace std;
const int N=1e6+50;
const int mod=998244353;
ll mgml(ll a,ll b,ll ans=1){
for(;b;b>>=1,a=a*a%mod) if(b&1) ans=ans*a%mod;
return ans;
}
int gcd(int x,int y){return y?gcd(y,x%y):x;}
int n,m,k,fac[N],inv[N],finv[N],phi[N],pr[N],v[N];
ll C(int x,int y){return (x<y||y<0)?0:1LL*fac[x]*finv[y]%mod*finv[x-y]%mod;}
int calc(int n,int m,int ans=0){
for(int i=0;i<=n-m&&i*k<=m;++i) ans=(ans+(i&1?mod-1LL:1LL)*C(m-i*k+n-m-1,n-m-1)%mod*C(n-m,i)%mod)%mod;
return 1LL*ans*n%mod*mgml(n-m,mod-2)%mod;
}
int main(){
fac[0]=fac[1]=inv[0]=inv[1]=finv[0]=finv[1]=phi[1]=1;
for(int i=2;i<N;++i) fac[i]=1LL*fac[i-1]*i%mod,inv[i]=1LL*inv[mod%i]*(mod-mod/i)%mod,finv[i]=1LL*finv[i-1]*inv[i]%mod;
for(int i=2;i<N;++i){
if(!v[i]) pr[++pr[0]]=i,phi[i]=i-1;
for(int j=1;i*pr[j]<N;++j){
v[i*pr[j]]=1;
if(i%pr[j]) phi[i*pr[j]]=phi[i]*phi[pr[j]];
else {phi[i*pr[j]]=phi[i]*pr[j];break;}
}
}
int T;scanf("%d",&T);
while(T--){
scanf("%d%d%d",&n,&m,&k);int ans=0;++k;
for(int i=1,lim=gcd(n,m);i*i<=lim;++i) if(lim%i==0){
ans=(ans+1LL*phi[i]*calc(n/i,m/i)%mod)%mod;
if(i*i!=lim) ans=(ans+1LL*phi[lim/i]*calc(n/lim*i,m/lim*i)%mod)%mod;
}
printf("%lld
",1LL*ans*mgml(n,mod-2)%mod);
}
return 0;
}
省选模拟27#
1.飞行棋##
概率dp
求出dp[i][j]表示到第i轮,初始位置在j此时到达n的概率.
转移显然
然后枚举每个点的胜利轮数,把其他点在此之后胜利的概率相加再相乘计算答案.
模拟轮数多了后可以接近正确答案.
2.字符串难题##
dp
首先n的范围很适合容斥.
考虑一种奇加偶减的容斥.
可以发现串做的贡献就是不同长度公共前缀的个数.
(L=sum_{iin S}-1^{|i|-1}dp[i]2^{cnt[|S|-i]})
(cnt[i])为串集合(i)中?个数.
问题变为给定若干个串的集合,求所有公共前缀的个数.
设(f[i])表示长度为i的公共前缀的个数.
设(ch[i][0/1])为是否全不为0/1.
转移(f[i]=f[i-1]*(ch[i][0]+ch[i][1]))
表示这一位可以向两个方向转移.
最后(dp[i]=sumlimits_{j=1}{minlen}dp[j]*2^{siz[maxlen]-siz[j]})
(siz[i])为串集合前i位中?个数的前缀和.
表示这种长度的后缀在剩下的所有问号所有被选择情况中都存在.
3.障碍雷达##
决策单调性dp+cdq
可以发现对于一个导弹一定只有选择和不选择两种情况.
因为越选择对答案的增量越多.
所以(O(n^2))可以列出来了.
(dp[i]=max(dp[j]+calc(i,j))[check(i,j)==1])
你感性理解的话这玩意是一定有单调性的.
假如上一个都能选i了,这个选后面的才一定不吃亏啊.
所以用决策单调性优化一下.
又因为需要前面的dp值来更新,所以再套上一个cdq.
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e6+50;
const ll inf=1e18;
int n;ll dp[N];
struct point{
ll x,y,c;
int id;
}dat[N];
void solve(int l,int r,int L,int R){// 用[l,r]更新[L,R]
if(L>R) return;
int mid=(L+R)>>1;
ll mx=-inf,pos=0;
for(int i=l;i<=r;++i){
if(dat[i].x+dat[i].y<=dat[mid].x-dat[mid].y){
ll res=dp[dat[i].id]+dat[mid].y*dat[mid].y-dat[mid].y*dat[mid].c;
if(res>mx) mx=res,pos=i;
}
else if(dat[i].x+dat[i].y>dat[mid].x+dat[mid].y) ;
else{
ll res=(dat[i].x+dat[i].y-dat[mid].x+dat[mid].y)/2;
res=dp[dat[i].id]+dat[mid].y*dat[mid].y-dat[mid].y*dat[mid].c-res*res;
if(res>mx) mx=res,pos=i;
}
} if(mx>dp[dat[mid].id]) dp[dat[mid].id]=mx;
solve(l,pos,L,mid-1);
solve(pos,r,mid+1,R);
}
void cdq(int l,int r){
if(l==r) return dp[dat[l].id]=max(dp[dat[l].id],dat[l].y*dat[l].y-dat[l].y*dat[l].c),void();
int mid=(l+r)>>1;
cdq(l,mid);
sort(dat+l,dat+mid+1,[](point a,point b){return a.x+a.y<b.x+b.y;});
sort(dat+mid+1,dat+r+1,[](point a,point b){return a.x-a.y<b.x-b.y;});
solve(l,mid,mid+1,r);
cdq(mid+1,r);
}
void work(){
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%lld%lld%lld",&dat[i].x,&dat[i].y,&dat[i].c),dat[i].x<<=1,dat[i].y<<=1,dat[i].c<<=1,dp[i]=0;
sort(dat+1,dat+n+1,[](point a,point b){return a.x<b.x;});
for(int i=1;i<=n;++i) dat[i].id=i;
cdq(1,n); ll ans=0;
for(int i=1;i<=n;++i) ans=max(ans,dp[i]);
printf("%.2Lf
",1.0L*ans/4);
}
int main(){
int T;scanf("%d",&T);
while(T--) work();
return 0;
}
省选模拟28#
1.战略游戏##
分治NTT
以被所有经过的路径作为问题的开口.
考虑路径分为两种情况.
有lca,以及是树上的一条祖先链.
假如我们知道了这条路径,考虑怎么求解.
设为((u,v))
由于其他边只允许一条路径经过.
因此对于u,v的儿子都只允许在子树中选择一个点作为起点/终点(看哪个大哪个小咯).
考虑生成函数就是(L=prod(siz x+1))
可以分治NTT求解.
由于每个点都只有作为一次儿子,因此复杂度(O(nlog^2))
选择了i路径的方案数就是最后的([x^i]F(x)).
剩下的k-i个人就老老实实呆在u这个位置就好了.
(f[u]=sumlimits_{i=0}^{min(son[u],k)}C(k,i)[x^i]F(x))
这样对于路径是第一种情况的在lca处就可以统计了.
对于第二种情况,(g=ffrac{(n-siz[u])x+1}{siz[son_u]x+1})
可以(O(项数))计算出来答案.
这里如果这样计算的话会被菊花卡成(O(n^2)).
所以考虑变化的(siz[son_u])最多不会超过(sqrt n)种.
因此只需要把每个点的儿子的siz去下重复杂度就对了.
因为每个点的(deg)最多有(sqrt n)种.
(deg-1)儿子个数也只有(sqrt n)种.
这里的复杂度(O(nsqrt n).
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cmath>
#define ll long long
using namespace std;
const int N=150000+50;
const int mod=998244353;
inline int rd(register int x=0,register char ch=getchar(),register int f=0){
while(!isdigit(ch)) f=ch=='-',ch=getchar();
while(isdigit(ch)) x=(x<<1)+(x<<3)+ch-48,ch=getchar();
return f?-x:x;
}
ll mgml(ll a,ll b,ll ans=1){for(;b;b>>=1,a=a*a%mod) if(b&1) ans=ans*a%mod;return ans;}
int n,k,B;
int head[N],nxt[N<<1],to[N<<1],rev[N],BIT[N],A[20][N],f[N],g[350][N],siz[N],ord[N],fac[N],inv[N],finv[N],bel[N];
inline void lnk(int x,int y){
to[++B]=y,nxt[B]=head[x],head[x]=B;
to[++B]=x,nxt[B]=head[y],head[y]=B;
}
void NTT(int *a,int len,int opt){
for(int i=0;i<len;++i){
rev[i]=(rev[i>>1]>>1)|((i&1)<<BIT[len]-1);
if(i<rev[i]) swap(a[i],a[rev[i]]);
}
for(int i=1;i<len;i<<=1)for(int j=0,wn=mgml(3,(mod-1)/(i<<1));j<len;j+=i<<1)for(int k=0,x,y,w=1;k<i;++k,w=1LL*w*wn%mod)x=a[j+k],y=1LL*w*a[j+k+i]%mod,a[j+k]=(x+y)%mod,a[j+k+i]=(x-y+mod)%mod;
if(opt==1) return;
reverse(a+1,a+len);for(int i=0,Inv=mgml(len,mod-2);i<len;++i) a[i]=1LL*a[i]*Inv%mod;
}
void solve(int l,int r,int depth){
int *a=A[depth],*b=A[depth+1],len=1<<(int)(log2(r-l+1)+1);
for(int i=0;i<len;++i) a[i]=0;
if(l==r) return a[0]=1,a[1]=ord[l],void();
int mid=(l+r)>>1;
solve(l,mid,depth+1);for(int i=0,lim=1<<(int)(log2(mid-l+1)+1);i<lim;++i) a[i]=b[i];solve(mid+1,r,depth+1);for(int i=1<<(int)(log2(r-mid)+1);i<len;++i) b[i]=0;
NTT(a,len,1);NTT(b,len,1);for(int i=0;i<len;++i) a[i]=1LL*a[i]*b[i]%mod;NTT(a,len,-1);
}
void mul(int *a,int &n,int siz){
a[++n]=0;for(int i=n-1;~i;--i) a[i+1]=(a[i+1]+1LL*siz*a[i]%mod)%mod;
}
void div(int *a,int &n,int siz){
a[n--]=0;for(int i=0;i<n;++i) a[i+1]=(a[i+1]-1LL*siz*a[i]%mod+mod)%mod;
}
void dfs1(int x,int prt){
siz[x]=1;int tot=0;
for(int i=head[x];i;i=nxt[i]) if(to[i]!=prt) dfs1(to[i],x),siz[x]+=siz[to[i]];
for(int i=head[x];i;i=nxt[i]) if(to[i]!=prt) ord[++tot]=siz[to[i]]; if(!tot) return f[x]=1,void();
solve(1,tot,1); for(int i=0;i<=tot&&i<=k;++i) f[x]=(f[x]+1LL*A[1][i]*fac[k]%mod*finv[k-i]%mod)%mod;
sort(ord+1,ord+tot+1);int num=unique(ord+1,ord+tot+1)-(ord+1);if(n-siz[x]) mul(A[1],tot,n-siz[x]);
for(int i=head[x];i;i=nxt[i]) if(to[i]!=prt) bel[to[i]]=lower_bound(ord+1,ord+num+1,siz[to[i]])-ord;
for(int i=1;i<=num;++i){
div(A[1],tot,ord[i]);
for(int j=0;j<=tot&&j<=k;++j) g[i][x]=(g[i][x]+1LL*A[1][j]*fac[k]%mod*finv[k-j]%mod)%mod;
mul(A[1],tot,ord[i]);
}
}
int ans;
int dfs2(int x,int prt,int anc){
ans=(ans+1LL*f[x]*anc%mod)%mod; int ret=0;
for(int i=head[x],tt;i;i=nxt[i]) if(to[i]!=prt) tt=dfs2(to[i],x,(anc+g[bel[to[i]]][x])%mod),ans=(ans+1LL*ret*tt%mod)%mod,ret=(ret+tt)%mod;
return (ret+f[x])%mod;
}
int a[N],b[N];
int main(){//freopen("game5.in","r",stdin);
fac[0]=fac[1]=inv[0]=inv[1]=finv[0]=finv[1]=1;
for(int i=2;i<N;++i) fac[i]=1LL*fac[i-1]*i%mod,inv[i]=1LL*inv[mod%i]*(mod-mod/i)%mod,finv[i]=1LL*finv[i-1]*inv[i]%mod;
n=rd();k=rd();for(int i=0,j=1;j<N;++i,j<<=1) BIT[j]=i;
if(k==1) return printf("%lld
",1LL*n*(n-1)/2%mod),0;
for(int i=1;i<n;++i) lnk(rd(),rd());
dfs1(1,0);dfs2(1,0,0);
printf("%d
",(ans%mod+mod)%mod);
return 0;
}
2.小b爱取模##
贪心
首先把区间加变为差分.
设差分数组为c.
在(\% k)意义下.
那么这个位置要么+k-c[i],要么-c[i].
令(c[i]=k-c[i])
此时变成了+c[i],c[i]-k.
此时的这个c[i]数组不是(\% k)的意义下了.
它是有正有负的.
然后我们发现答案就是(sumlimits_{i=1}^nmax(0,c[i])).
因为+ 与 - 是相系的,也就是每一个正就对应着每一个负.
同时可以发现对于最优决策,一定不存在一个位置既+又-.
同时,
我们还要满足前缀和非负的基本条件.
那么考虑此时的c[i].
对于任意的c[i]如果变成负的都只会造成相同的-k的损失.
但是对于越大的c[i],对于我们的答案它原本的贡献就越大.
那么对于相同的损失,我们肯定优先选择贡献大的进行变换.
同时对于同样的c[i],选取后缀一定不会更劣.
#include<iostream>
#include<cstring>
using namespace std;
int k,n,a[11111111],t[11111111],ans;char s[11111111];
int main(){
scanf("%d%s",&k,s+1);s[0]='0';n=strlen(s+1);
for(int i=1;i<=n;++i)a[i]=(k-s[i]+s[i-1])%k;
for(int i=1;i<=n;++i)t[i]=a[i]+t[i-1];
for(int x=k-1,mn;mn=111111111,~x;--x){
for(int i=n;i;--i){
mn=min(mn,t[i]);
if(mn>=k&&a[i]==x)mn-=k,a[i]-=k;
}
for(int i=1;i<=n;++i)t[i]=t[i-1]+a[i];
}for(int i=1;i<=n;++i)ans+=max(a[i],0);cout<<ans;
}
3.小b爱实数##
?
题目给出f是6位小数,显然让变(longlong)用的.
发现题目要求的是(frac{cnt[r]-cnt[l-1]}{r-(l-1)}==f).
大力挪式子就可以把式子拆成(cnt[r]-rf==cnt[l-1]-(l-1)f).
发现对于同一个(r)来说,能形成最小l一定是是两边相差最小的两项.
求前驱后继,set维护.
然后把这个与(f)的差和答案取min就可以了.
注意,这里只需要取(min),所以如果说你傻傻的用个set维护最小值,你就死了.
题解给出来的做法是划式子的时候变成了另一种形式.
(frac{cnt[r]-r-(cnt[l]-l)}{r-l}==0)
问题转换成了求两点斜率绝对值最小.
按(y),排序,相邻点斜率绝对值最小.
可以通过反证得到.
省选模拟29#
1.circle##
竞赛图
首先考虑合法情况.
首先应该满足k个点没环,其次由于保证了那n-k个点没有环.
如果把图分成这样的两部分.
就可以发现,因为竞赛图的特殊性质,它一定是这样的东西.

那考虑一定要删的点的情况.
就是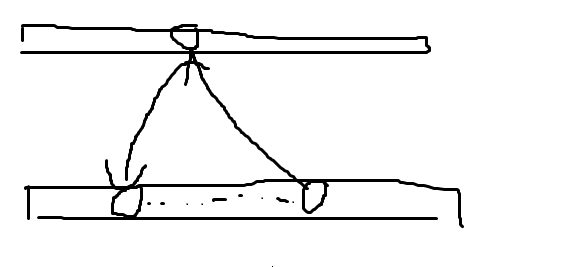
也就是说,可以得到,如果这个点不是这样的情况.
那么一定是从某个k个点中的一个点i分开左边是对它的入边,右边是对它的出边.
既然这样每个点维护这个点i,然后跑LCS就可以了.
2.生成膜咒##
发现首先对于每次添加字符会多出来n个串.
然后发现真正多的串只有这n个串的最长后缀那个子串,其他的是上次的增量.
考虑这些子串的新增深度,就是它的border个数.
改变枚举对象,从枚举子串再求border变成枚举border然后看它在几个子串里出现过.
容易发现这样做就是在(sam)上不断跳(fa),然后对于每个(fa),它的贡献就是(endpos*(len[i]-len[fa[i]]).
3.simulate##
模拟
首先.
题解说轮数根本没用,可以一个点一个点计算.
说的很对,但考场根本没往这个方向想.
然后对于向左边的贡献,可以通过分类讨论做出来.
对于右边的贡献就贡献呗,反正还没有处理完呢.
省选模拟30#
1.任凭风浪起,稳坐钓鱼台##
2.任凭风浪起,稳坐钓鱼台(续)##
3.鱼和熊掌不可兼得##
?
先rand出来一组(ans=0)的方案.
把边分成若干个集合使得集合内点没有重合.
按(i+j%n)分.
对于每个集合,二分的找到每条有用的边.
然后dfs找环,环两个方向检查一下.
省选模拟31#
1.Skip##
树状数组+静态凸包
我们先写出来裸(O(n^2))dp.
发现calc(i,j)中有ij形式的成分.
果断凸包维护.
把(j,val(j))看作点,题目要求截距最大.
维护上凸包.
打完后发现样例一个也过不去.
原来转移有条件:满足(a)单调递增.
那么就维护树状数组而后在(log)个凸包里查询,修改.
(O(nlog^2))
但是Kai586123的做法是按照a排序而后cdq一下.
按横坐标归并一下左右区间,然后扫到左区间的点建凸包,扫到右区间的点二分斜率似乎不是更新答案.
因为转移只会按照a升序转移,所以这样做是对的.
2.String##
dp
很遗憾最后没有能打出来.
先考虑80分状压dp做法的思路.
其实这个思路很朴素,只是我认为很难打.
依次枚举每个位置选的是哪种字符.
然后计算出来在前t位确定的情况下后面有多少种情况.
如果当前就>n就说明这一位不能再往下填了.
考虑怎么计算在已知前t位的情况下计算后面的情况数.
设现在已确定cnt种颜色.显然k>=cnt才行.
然后对于k-cnt的剩下的颜色随便选就行,反正我们并不关注.
然后对这k种颜色全排列.
这也是我意想不到的地方.
我没想到k=8支持这种骚操作.
现在就找到所有这k个位置的颜色还剩多少个能用.
再记录一下上个位置是谁就可以记忆化dp了.
想要ac的话.
能够发现k=8的最大情况已经>1e18了.
所以对于k>8的情况,前面一定是ababababab.....cdcdcdcdcd....efefefefefef一直到k<=8为止.
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll inf=1e18+10;
int k,fir='a',p[10];
ll n;
char s[50];
int vis[300];
map<vector<int>,ll> mp[10];
ll dfs(vector<int> x,int lst){
int val=x[lst]; sort(x.begin(),x.end());
for(int i=0;i<k;++i) if(val==x[i]){ lst=i; break;}
auto it=mp[lst].find(x);
if(it!=mp[lst].end()) return it->second; ll r=0;
for(int i=0;i<k;++i) if(x[i]&&i!=lst){
--x[i],r+=dfs(x,i),++x[i];
if(r>inf) return mp[lst][x]=inf;
}
return mp[lst][x]=r;
}
inline ll A(int n,int m,ll r=1){
for(int i=1;i<=m;++i){
r=r*(n-i+1);
if(r>inf) return inf;
}
return r;
}
inline ll calc(int t){//已经确定t位
vector<int> now; now.resize(k); int cnt=0; ll r=0;
for(int i='a';i<='z';++i) vis[i]=0;
for(int i=1;i<=t;++i) ++vis[s[i]];
for(int i=1;i<=k;++i) p[i]=0;
for(int i='a';i<='z';++i) if(vis[i]) p[++cnt]=i;
if(cnt>k) return 0;
sort(p+1,p+k+1);
do{
int lst=0; double tmp; ll a,b;
for(int i=1;i<=k;++i) now[i-1]=i-vis[p[i]];
for(int i=1;i<=k;++i) if(now[i-1]<0) goto nxt;
for(int i=1;i<=k;++i) if(p[i]==s[t]){ lst=i-1; break;}
a=dfs(now,lst); b=A(26-cnt-(fir-'a'),k-cnt);
tmp=1.0*a*b; r+=a*b;
if(tmp>inf||r>inf) return inf; nxt:;
}while(next_permutation(p+1,p+k+1));
return r;
}
int main(){
scanf("%d%lld",&k,&n);
while(k>8){
for(int i=1;i<=2*k-1;++i)
if(i&1) putchar(fir);
else putchar(fir+1);
fir+=2; k-=2;
}
const int len=k*(k+1)/2;
vector<int> t; t.resize(k);
for(int i=0;i<k;++i) mp[i][t]=1;
for(int i=1,j;i<=len;++i){
for(j=fir;j<='z';++j) if(j!=s[i-1]){
s[i]=j; ll tmp=calc(i); n-=tmp;
if(n<=0){ n+=tmp; break; }
}
if(j>'z') return puts("-1")&0;
}
return printf("%s",s+1)&0;
}
3.Permutation##
?
有个(O(n^2))的dp是显然相邻的序列一定会在某个位置开始不同.
那么我们枚举这个位置j,以及这个位置的数x.
下个序列这个位置一定是x+1.
并且是这样的.
........x n-j+2 n-j+3 .... n
........x+1 x+2 x+3 x+4 .....
只有这样才会使得两个序列相邻.
那么后面序列已知.
前面随便选的方案数是(C(x-1,j-1)).
用这个组合数*m位置的差的绝对值.
优化.
发现m位置的差的绝对值是一个|x-j+r|的形式.
所以变为枚举(x-j(a)),再枚举j(b).
组合数就是(C(a+b-1,b-1)=C(a+b-1,a))
就变成了一列的组合数就可以(O(1))了.
上下界什么的挺重要的.
这个改变枚举对象也很重要的.
省选模拟32#
1.送你一道签到题##
min_25筛
(i^k)是积性函数而且也是低阶多项式,(sigma(d))也是积性函数,所以可以用min_25筛法.
但min_25筛法除了积性函数,低阶多项式,还要求快速求出(f(p^k)).
发现对于(p^k),(sigma(d1)sigma(d2)...)只与(k)有关,与p无关.
问题等价于将(k)分配到m个位置的方案数,可以有位置不放.
这样的东西没有数论函数可以求出,考虑到(>1)位置不会超过50位,因此dp求出(dp[K]).
2.神犇##
(trie)
首先设出三个人的前缀和,对于一个确定的r,那么l合法的条件是
转化成前缀异或和后,可以通过容斥求出所有合法的前缀和.
具体的就是奇减偶加.
同时考虑到若(ABC)中任意两个相同等价于三个都相同.
所以真正的(trie)里元素个数是(U-A-B-C+2*ABC).
3.开挂##
(dp)
枚举出所有的本质不同的矩形来.
为了不让矩形有重复,保证四条边都有人.
那么发现因为四条边都有人,所以最优一定是左上右下放/左下右上放.
而且放置方式相同,方案数也相同.
那么现在已经知道哪里可以放,哪里不能放了.
要求四条边必须有放的位置,里边随便.
考虑(dp).
设(dp[2][2][2][2][2][2][2])表示滚动,上下左右是否放了人,第一种情况,第二种情况能否覆盖这种方案的方案数.
转移就枚举这个位置放不放.
最后答案是(dp[0][0]+dp[0][1]+dp[1][0]).
省选模拟33#
1.盗梦空间##
虚树+(dp)
对于每次询问的关键点建出虚树.
答案点的出现位置有三种情况.
(0.虚树根的上边的点)
1.虚树上的点
2.未出现的在某个子树里
3.在相邻虚树点中间
首先跑多源点最短路求出每个点离坏点距离(dis).
1可以直接统计答案.
2需要对每个节点开个(multiset)统计子树最长链,然后删掉那些在虚树上的子树再统计答案.
3考虑求出一个中间点v满足下边与儿子统计答案,上边与父亲统计答案.
对于第一种情况.
需要求出dis[son]+dep[son]+dep[u]-2dep[x].
所以维护子树dep[u]-2dep[x]的最大值.
对于第二种情况.
需要求出dis[fa]+dep[u]-dep[fa]
所以维护子树dep[u]的最大值.
同时发现需要去掉自己的贡献,于是倍增维护.
倍增数组维护父亲去掉我的贡献时的贡献.
细节稍多,实现比较麻烦.
2.爱乐之城##
莫比乌斯反演
题意:
给定
在线求
首先求出(f(x),g(x))
增量构造.
每次x++
总改变量是(nln)的.
对于
因为对于一个数n,与n互质数总是成对出现和为n的.
所以
同理进行增量构造.
考虑对第二部分莫比乌斯反演.
设(h(x))表示所有情况下gcd为x的倍数的贡献和.
(G(x))为后面那个大东西.
由莫比乌斯反演知
那么有
改变枚举对象
设(r[n]=sumlimits_{d|n}f(d)mu(n/d))
考虑增量构造答案.
发现每次改变的都只有(a[n])的倍数位置.
因此总改变次数(nln)次.
3.星际穿越##
省选模拟34#
1.倚天剑的愤怒##
贪心
题目要求前缀和(>=0).
首先如果倒着加入的话就变成了贪心.
那么考虑一个(O(n^2))的dp为(dp[i][j]),倒着考虑到i,放了j把剑时的后缀和和后缀最小值.
因为在开头加入一个元素所有的后缀值都会发生改变.
所以这样做的是对的.
考虑正解
还是倒着扫,把权值<0的剑放入大根堆中,每次扫到权值>0的剑就尝试抵消若干把负剑的权值.
最后剩下的负剑就只能够靠初始值来消灭了,因此二分能消掉多少判断就行.
2.原谅##
模拟
一种接近乱搞的正解.
考虑枚举最终停在了哪种权值.
那么>该权值的点一定都被放入了.
一部分该权值的点也被放入了.
那么考虑先把>该权值的点全部放入.
假如能联通成一个的话,我们尝试多放入一些该权值的点累加答案.
也就是枚举所有该权值的点判断是否和大连通块有连边,有就从这个点dfs把所有这个权值与它相邻的点都放进去.
假如不能联通成一个的话,就一定要把此时不连通的两个连通块中间的路径全部打通.
那么因为不能联通成一个说明路径中间的权值一定<该权值.
那最终停在的权值也就一定<=路径的min了.
这样一直向后模拟.
复杂度(O(n+m)).
3.收集##
?
考虑姊妹问题:从该点出从该点回来的最小时间.
这样就会发现,最优情况每条边一定都会上下经过两次.
那么问题转化成了求边权和*2-直径长度.
求边权和.
有一个很大神的做法是,按照dfs序(环)排序答案是相邻点的距离之和.
求直径长度.
可以虚树统计,不过我们发现由于每次只改变一个点的优秀性质.
可以记录每个点的出现情况,然后线段树分治.
可是我想不到姊妹问题就GG了.
省选模拟35#
1.two##
线段树
对于给定的一条边,发现在另一棵树上的删边情况只有两种.
所以把所有边二元组插到另一棵树的两棵线段树里(因为用的是ta的dfn序).
在第一颗线段树u处插v,第二颗v处插u.
查询时查询区间内线段树里另一维(>l/<r)的所有.
可以用单调指针+pop_back搞.
删除后就打上懒标记防止重复计算.
实现起来如果想要简便一些需要一些脑子来优化.
2.bracket##
点分治+FFT
第一次打点分治.
我们知道括号序列合法条件是前缀和始终(>=0).
可是还有神仙指出还有一种从后往前的判断方式:后缀最大值即为合法.
感性的证明方法是开始时max=0,后面若想要成为后缀最大值最少也只能是完整的括号.
中间可能会有空出的左括号增加后缀.
同理对于右序列来说合法的情况还等价于前缀最小值.
理解方式与上边类似.
因此在子树里求出有多少合法的左右括号序列,以及他们的贡献,以及把左右括号赋成+-1时,他们的值.
贡献就是之前出现的后缀最大值个数.
感性理解就是每次新出现的一个相同的后缀最大值就表明中间是一个合法的括号匹配.
把值相反数的左右序列的贡献的个数卷积起来.
但会有某棵子树自己卷了自己的情况.
此时就枚举每个子树容斥掉自己的方案.
需要注意的是
1.根只能给左右序列中的一个.我给的左.
2.容斥掉子树时,父亲自己当左序列的合法情况不能给记录下来.需要特判.
3.淀粉质进入这个点当根时(siz)之类的东西并不是正确的,需要再跑个(dfs).
(对拍用)
#include<cstdio>
#include<cmath>
#include<vector>
#include<algorithm>
#define ll long long
using namespace std;
const int N=3e5+10;
const double PI=acos(-1);
inline int rd(register int x=0,register char ch=getchar(),register int f=0){
while(ch<'0'||ch>'9') f=ch=='-',ch=getchar();
while(ch>='0'&&ch<='9') x=(x<<1)+(x<<3)+ch-48,ch=getchar();
return f?-x:x;
}
struct complex{
double real,imag;
complex(){}
complex(double real,double imag):real(real),imag(imag){}
}a[N],b[N];
complex operator + (complex a,complex b){return complex(a.real+b.real,a.imag+b.imag);}
complex operator - (complex a,complex b){return complex(a.real-b.real,a.imag-b.imag);}
complex operator * (complex a,complex b){return complex(a.real*b.real-a.imag*b.imag,a.real*b.imag+a.imag*b.real);}
int n,B,rt,Mx,size;
int head[N],to[N<<1],nxt[N<<1],w[N],rev[N],BIT[N],LOG[N],vis[N],siz[N];
vector<int> ans,dec,cnt_l[N<<1],cnt_r[N<<1];
void lnk(int x,int y){
to[++B]=y,nxt[B]=head[x],head[x]=B;
to[++B]=x,nxt[B]=head[y],head[y]=B;
}
void FFT(complex *a,int len,int opt){
for(int i=0;i<len;++i){
rev[i]=(rev[i>>1]>>1)|((i&1)<<BIT[len]-1);
if(i<rev[i]) swap(a[i],a[rev[i]]);
}
for(int i=1;i<len;i<<=1){
complex wn(cos(PI/i),sin(PI/i));
for(int j=0;j<len;j+=i<<1){
complex w(1,0),x,y;
for(int k=0;k<i;++k,w=w*wn)
x=a[j+k],y=w*a[j+k+i],a[j+k]=x+y,a[j+k+i]=x-y;
}
}
if(opt==1) return;
reverse(a+1,a+len);
for(int i=0;i<len;++i) a[i].real/=len,a[i].imag/=len;
}
void findrt(int x,int prt){
siz[x]=1;int mx=0;
for(int i=head[x];i;i=nxt[i]) if(to[i]!=prt&&!vis[to[i]])
findrt(to[i],x),siz[x]+=siz[to[i]],mx=max(mx,siz[to[i]]);
mx=max(mx,size-siz[x]);
if(mx<Mx) Mx=mx,rt=x;
}
int mx,mn;
void dfs(int x,int prt,int l,int r,int mx_l,int mn_r,int gx_l,int gx_r,int opt=0){//gx_l变成最大值的次数,gx_r变成最小值的次数
l+=w[x];
if(l>mx_l) mx_l=l,cnt_l[l].push_back(0),gx_l=1;
else if(l==mx_l) cnt_l[l].push_back(gx_l++);
if(!opt){
r+=w[x];
if(r<mn_r) mn_r=r,cnt_r[N+r].push_back(0),gx_r=1;
else if(r==mn_r) cnt_r[N+r].push_back(gx_r++);
}//printf("x:%d(%d) prt:%d l:%d r:%d mx_l:%d mn_r:%d gx_l:%d gx_r:%d opt:%d
",x,w[x],prt,l,r,mx_l,mn_r,gx_l,gx_r,opt);
for(int i=head[x];i;i=nxt[i]) if(prt!=to[i]&&!vis[to[i]]) dfs(to[i],x,l,r,mx_l,mn_r,gx_l,gx_r);
}
void solve(int x,int pre=0){
//printf("准备开始dfs啦!!! solve :%d %d
",x,pre);
int len=1ll<<(LOG[(siz[x]+1)]+1);dec.resize(len);
for(int i=0;i<len;++i) cnt_l[i].resize(0),cnt_r[N-i].resize(0),dec[i]=0;
pre?dfs(x,pre,w[pre],0,max(0,w[pre]),0,1,1,0):dfs(x,0,0,0,0,0,1,1,1);
if(!pre) for(int i=0;i<(int)cnt_l[0].size();++i) dec[cnt_l[0][i]]++;
//puts("DFS结果揭晓!!");
//for(int i=0;i<len;++i) for(int j=0;j<(int)cnt_l[i].size();++j) printf("cnt_l[%d][%d]=%d ",i,j,cnt_l[i][j]);puts("");
//for(int i=0;i<len;++i) for(int j=0;j<(int)cnt_r[N-i].size();++j) printf("cnt_r[%d][%d]=%d ",-i,j,cnt_r[N-i][j]);puts("");
for(int i=0;i<len;++i) if(cnt_l[i].size()&&cnt_r[N-i].size()){
for(int j=0;j<len;++j) a[j]=complex(0,0),b[j]=complex(0,0);
for(int j=0;j<(int)cnt_l[i].size();++j) a[cnt_l[i][j]].real++;
for(int j=0;j<(int)cnt_r[N-i].size();++j) b[cnt_r[N-i][j]].real++;
//printf("FFT前的最后一点check 了
");
//for(int j=0;j<len;++j) printf("a[%d]=%lf
",j,a[j].real);puts("");
//for(int j=0;j<len;++j) printf("b[%d]=%lf
",j,b[j].real);puts("");
FFT(a,len,1); FFT(b,len,1); for(int j=0;j<len;++j) a[j]=a[j]*b[j]; FFT(a,len,-1);
//for(int j=0;j<len;++j) printf("ans[%d]=%lf
",j,round(a[j].real));
if(i==0) for(int j=0;j<len;++j) dec[j]+=round(a[j].real);
else for(int j=0;j<len-1;++j) dec[j+1]+=round(a[j].real);
}//puts("Done");
//for(int i=0;i<len;++i) printf("%d ",dec[i]);puts("");
}
void sea(int x,int prt){
siz[x]=1;
for(int i=head[x];i;i=nxt[i]) if(to[i]!=prt&&!vis[to[i]]) sea(to[i],x),siz[x]+=siz[to[i]];
}
void divide(int x){//规定:左边有x 右边没x
//printf("divide :%d
",x);
vis[x]=1;
//printf("开始 solve (x)
");
solve(x);
//printf("结束 solve (x)
");
//for(int i=0;i<(int)dec.size();++i) printf("dec[%d]=%d ",i,dec[i]);puts("");
for(int i=0;i<(int)dec.size();++i) ans[i]+=dec[i];
//for(int i=0;i<(int)ans.size();++i) printf("%d ",ans[i]);puts("");
for(int i=head[x];i;i=nxt[i]) if(!vis[to[i]]){
solve(to[i],x);
for(int j=0;j<(int)dec.size();++j) ans[j]-=dec[j];
}
//printf("让我看看
");
//for(int i=0;i<(int)ans.size();++i) printf("%d ",ans[i]);puts("");
for(int i=head[x];i;i=nxt[i]) if(!vis[to[i]]) size=siz[to[i]],Mx=0x3f3f3f3f,findrt(to[i],0),sea(rt,0),divide(rt);
}
int main(){
//freopen("text.in","r",stdin);
//freopen("yesterday_T2.out","w",stdout);
for(int i=0,j=1;j<N;++i,j<<=1) BIT[j]=i;
LOG[0]=-1;for(int i=1;i<N;++i) LOG[i]=LOG[i>>1]+1;
n=rd();ans.resize((n+1)<<1);
for(int i=2;i<=n;++i) lnk(rd(),rd());
for(int i=1;i<=n;++i){
char ch=getchar();
while(ch!='('&&ch!=')') ch=getchar();
w[i]=ch=='('?1:-1;
}
size=n;Mx=0x3f3f3f3f;findrt(1,0);sea(rt,0);
divide(rt);
//puts("终于跳出solve了!!!!
");
int m=rd();
while(m--) printf("%d
",ans[rd()]);
return 0;
}
/*
6 1 2 2 6 4 2 3 4 1 5 ) ( ) ) ( )
3 1 2 3
*/
3.sum##
网络流
一个性质(结论):最优替换一定是一个只有两个质因子的合数,并且一定是一个(>sqrt n)一个(<sqrt n).
那么这样就可以二分图了.
先添加上所有质数的贡献.
然后对质数二分图.
连边条件是(f(x*y)>f(x)+f(y)),费用是(f(x*y)-f(x)-f(y)),流量是1.
然后跑最大费用可行流.